Приложение двойного интеграла в задачах геометрии и механики

Площадь области D находится по формуле

Координаты центра масс однородной пластинки (при плотности  = 1) находятся по формулам:

; .

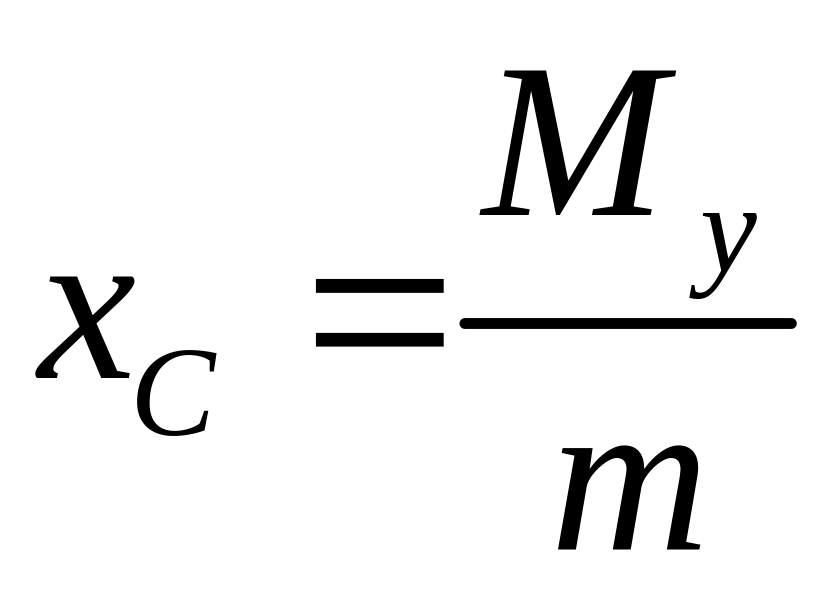Интегралы , называются статическими моментами пластинки относительно осей Ox и Oy, m – масса пластины равна .

Статическими моментами относительно осей Ох и Оу материальной точки Р(х, у) массы m_p называются величины M_x(P) и M_y(P) соответсвенно, определяемые равенствами M_x(P) = m_py, M_y(P) = m_px.

Статическим моментом системы точек называется сумма статических моментов точек, ее образующих.

Центром тяжести однородной пластины называется точка плоскости, обладающая следующим свойством: если в этой точке сосредоточить всю массу m заданной пластины, то статический момент этой точки относительно любой координатной оси будет равен статическому моменту всей пластины относительно той же оси.

Интегрирование в mathcad

Результат численного интегрирования ‑ это не точное, а приближенное значение интеграла, определенное с погрешностью, которая зависит от встроенной константы TOL. Чем она меньше, тем с лучшей точностью будет найден интеграл, но и тем больше времени будет затрачено на расчеты. По умолчанию TOL=0.001. Для того чтобы ускорить вычисления, можно установить большее значение TOL.

При вводе в редакторе MathCAD оператора численного интегрирования, вы, фактически, создаете самую настоящую программу, большая часть которой скрыта от вашего взора. В большинстве случаев об этом не приходится специально задумываться, можно полностью положиться на MathCAD. Но иногда может потребоваться умение управлять параметрами этой программы, как мы уже рассмотрели на примере выбора константы TOL. Кроме нее, пользователь имеет возможность выбирать сам алгоритм численного интегрирования. Для этого:

1. Щелкните правой кнопкой мыши в любом месте на левой части вычисляемого интеграла.

2 . В появившемся контекстном меню выберите один из четырех численных алгоритмов (см. рис.).

Обратите внимание, что перед тем как один из алгоритмов выбран впервые, как показано на рис., флажок проверки в контекстном меню установлен возле пункта AutoSelect (Автоматический выбор). Это означает, что алгоритм определяется MathCAD, исходя из анализа пределов интегрирования и особенностей подынтегральной функции. Как только один из алгоритмов выбран, этот флажок сбрасывается, а избранный алгоритм отмечается точкой.

В MathCAD 2001 запрограммированы четыре численных метода интегрирования:

- Romberg (Ромберга) - для большинства функций, не содержащих особенностей;

- Adaptive (Адаптивный) - для функций, быстро меняющихся на интервале интегрирования;

- Infinite Limit (Бесконечный предел) - для интегралов с бесконечными пределами;

- Singular Endpoint - для интегралов с сингулярностью на конце. Модифицированный алгоритм Ромберга для функций, не определенных на одном или обоих концах интервала интегрирования.

Старайтесь оставить выбор численного метода за MathCAD, установив флажок AutoSelect (Автоматический выбор) в контекстном меню. Попробовать другой метод можно, например, чтобы сравнить результаты расчетов в специфических случаях, когда у вас закрадываются сомнения в их правильности.

Если подынтегральная функция "хорошая", т. е. не меняется на интервале интегрирования слишком быстро и не обращается на нем в бесконечность, то численное решение интеграла не принесет никаких неприятных сюрпризов.

Для вычисления определенного интеграла необходимо выбрать знак интеграла из палитры или набрать его нажатием клавиши &. После этого следует вписать пределы интегрирования, подынтегральную функцию и переменную интегрирования. Mathcad успешно справляется с большинством интегралов, в том числе, с несобственными. Точность вычислений регулируется встроенной переменной TOL. По умолчанию ее значение установлено . Ниже приводится несколько примеров успешного вычисления несобственных интегралов, интеграла от быстро осциллирующей функции и интеграла от ступенчатой функции.

Здесь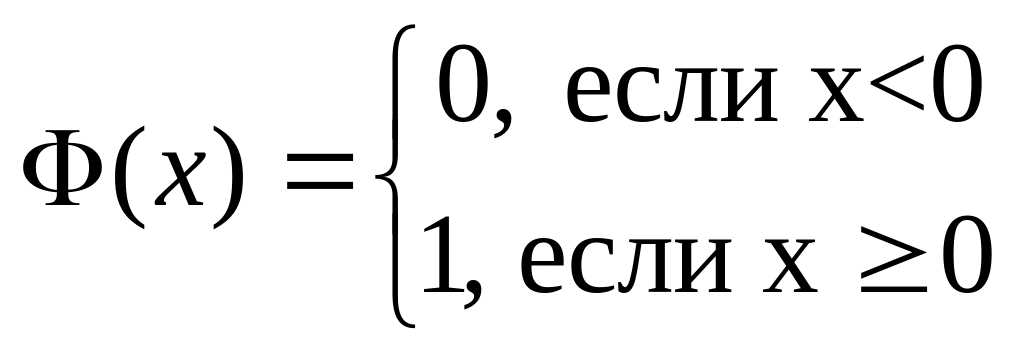

Зависимость результата от заданной точности вычислений представлена ниже

Для этого примера результат может быть получен также в символьном виде. Для этого вместо знака равенства необходимо нажать знак символического равенства Ctrl+.

В то же время в некоторых случаях несобственные интегралы вычисляются неправильно.

Хотя очевидно, что