Лекция 8. Сортировка массива

1. Задача сортировки

2. Сортировка обменами.

3. Сортировка выбором.

4. Сортировка вставками (включениями).

1. Задача сортировки

Под сортировкой последовательности понимают процесс перестановки элементов последовательности в определенном порядке. Цель такого упорядочения - облегчение дальнейшей обработки данных (в частности, задачи поиска). Поэтому задача сортировки - одна из наиболее важных внутренних задач программирования.

Сортировка является идеальным примером большого мно­жес­тва разно­образных алгоритмов, решения одной и той же задачи. Рассматривая раз­лич­ные методы сорти­ровок, видно, как изменение алгоритма приводит к но­вым, более эффективным по сравнению с простыми, решениям задачи сортиров­ки.

Кроме того, последовательности можно представить различными струк­ту­рами данных. Как и следует ожидать, эффективность алгорит­мов оказывается сильно зависящей от реализации последовательности.

Пусть нам дана последовательность элементов a₁, a₂, ... , a_n. Элементы этой последо­ва­тельности - данные произвольного типа, на котором определено отношение порядка “<<” (меньше) такое, что любые два различных элемента сравнимы. Сортировка означает перестановку элементов последовательности a_k1, a_k2, ... , a_kn такую, что

a_k1 << a_k2 << ... << a_kn.

Рассмотрим в качестве примера следующую задачу: Расположить в порядке возрастания последовательность из 4 чисел.

Сортировка массивов

Если последовательность a₁, a₂, ... , a_n реализована как массив a[1..n], вся она расположена в адресуемой памяти. Поэтому наряду с требованием эффектив­ности по времени основное тре­бование - экономное использование памяти. Это означает, что алгоритм не должен исполь­зо­вать дополнительных массивов и пере­сы­лок из массива a в эти массивы.

Постановка задачи сортировки в общем виде предполагает, что существуют только два типа действий с данными сортируемого типа: сравнение двух элементов (x < y) и пересылка элемента (x := y). Поэтому удобная мера сложности алгоритма сортировки массива a[1..n] по времени - количество сравнений C(n) и количество пересылок M(n).

Известные алгоритмы сортировки массивов делятся на простые и быстрые (эффективные). Независимо от принадлежности тому или иному классу, и простые, и быстрые алгоритмы используются на практике.

2. Простые алгоритмы сортировки

Простые алгоритмы сортировки имеют квадратичную оценку сложности по времени (T(n)= O(n²)) Мы рассмотрим три таких алгоритма: сортировку обменом, сортировку выбором и сортировку включениями.

Сортировка обменами

Основное действие сортировки обменами - сравнение двух элементов (чаще всего рядом стоящих) и, если результат сравнения отрицателен, перестановка их местами:

Если при i < j a[i] > a[j] то переставить a[i] и a[j]. В наиболее простом варианте срав­ни­ваются рядом стоящие элементы a[j] и a[j+1] :

Program BublSort;

Const n = 100;

Var a : array[1..n] of Real;

i, j : Integer; b : Real;

Begin

{ Блок ввода массива }

For i := n - 1 downto 1 do

For j := 1 to i do

If a[j] > a[j+1] then

begin

b := a[j+1]; a[j+1] := a[j]; a[j] := b

end;

{ Блок вывода массива }

End.

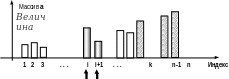
Рис 1. Алгоритм сортировки обменами

Алгоритм BublSort осуществляет n-1 линейный просмотр массива а. В результате каждого просмотра наибольший элемент просмотренной части массива «всплывает» на последнее место. Первый просмотр осуществляется во всем массиве, а каждый следующий – в диапазоне, на единицу меньшем. Таким образом, правая часть массива становится упорядоченной. На рисунке эти элементы – от a[k] до a[n] - заштрихованы серым. На каждом шаге просмотра сравниваются два рядом стоящих элемента. На рисунке – это элементы a[i] и a[i+1]. Если они расположены неправильно, алгоритм меняет их местами.