
3. Бинарный поиск в упорядоченном массиве
Задача поиска существенно упрощается, если элементы массива упорядочены. Стандартный метод поиска в упорядоченном массиве - это метод деления отрезка пополам, причем отрезком является отрезок индексов 1..n. В самом деле, пусть m (k < m < l) - некоторый индекс. Тогда если A[m] > b, далее элемент нужно искать на отрезке k..m-1, а если A[m] < b - на отрезке m+1..l.
Для того, чтобы сбалансировать количество вычислений в том и другом случае, индекс m нужно выбирать так, чтобы длины отрезков k..m, m..l были (приблизительно) равными. Описанную стратегию поиска называют бинарным поиском. Алгоритм бинарного поиска – один из алгоритмов, полученных в результате применения одного из общих методов разработки эффективных алгоритмов – метода «разделяй и властвуй».
Пример 3. Поиск элемента в упорядоченном массиве.
Program BinarySearch;
Const n = 100;
Var A : Array[1..n] of Real;
b : Real; Buffer : Real;
lt, rt, m : Integer;
Begin
{ Блок чтения упорядоченного массива A и элемента b }
lt := 1; rt := n;
Repeat
m := (lt + rt) div 2; Buffer := A[m];
If Buffer > b
then rt := Pred(m) else lt := Succ(m)
until (Buffer = b) or (rt < lt);
If A[m] = b
then Writeln(‘Индекс = ‘, m)
else Writeln( ‘Элемент не найден’)
End.

Рис 3. Бинарный поиск в упорядоченном массиве.
b – элемент, место которого необходимо найти. Шаг бинарного поиска заключается в сравнении искомого элемента со средним элементом A[m] в диапазоне поиска [k..l]. Алгоритм заканчивает работу при A[m] = b. Если A[m] > b, поиск продолжается слева от m, а если A[m] < b – справа от m. При l < k поиск завершается, и элемент не найден.
Нетрудно получить оценку числа С(n) сравнений метода. Пусть М - количество повторений цикла. Тогда М [log2 (n)] Поскольку на каждом шаге осуществляется 2 сравнения, в худшем случае
C(n) = 2[log2 n] = O(log2 n)
При n = 1000000 алгоритм совершает максимум 40 сравнений, в то время как линейный просмотр требует всех 1000000 сравнений.
5. Метод асинхронного просмотра
Некоторые задачи обработки массивов решаются методом, суть которого заключается в «параллельном» просмотре нескольких массивов, либо в просмотре одного массива с помощью нескольких «просматривающих» индексов, меняющих свои значения независимо. Классическая задача, эффективное решение которой достигается этим методом – задача слияния двух упорядоченных массивов.
Пример 4. Даны упорядоченные массивы А[1..n] и В[1..m]. Построить упорядоченный массив С, содержащий как все элементы массива A, так и все элементы массива В.
Program Merging;
Const n = 100;
Type Vector = array[1..n]of Integer;
Var A, B, C: Vector;
mA, mB, mC, i,j,k,l: Integer;
Begin
Read(mA);
For i := 1 to mA do read(A[i]) ;
{Ввод размера массива В и его элементов};
i:=1; j:=1; k:=1;
While (i <= mA) and (j <= mB) do begin
If A[i]<=B[j]
then begin C[k] := A[i]; Inc(i) end
else begin C[k] := B[j]; Inc(j) end;
Inc(k)
end;
For l := i to mA do begin C[k] := A[l]; Inc(k) end;
For l := j to mB do begin C[k] := B[l]; Inc(k) end;
mC := k-1;
end;
{Вывод массива С}
End.
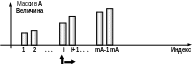
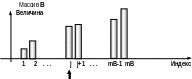

Рис 4. Слияние двух массивов методом асинхронного просмотра.
Алгоритм представлен процедурой Merge. Ее параметры – размеры массивов и собственно массивы. Перед слиянием «просматривающие индексы» i, j, k устанавливаются на 1. Шаг алгоритма заключается в сравнении рассматриваемых элементов сливаемых массивов А и В. В результирующий массив С копируется меньший из сравниваемых элементов, и соответствующие индексы инкрементируются. На рисунке показаны результаты первых 4-х шагов работы алгоритма, а также k-тый шаг. Асинхронный просмотр осуществляется, пока один из массивов не окажется просмотренным полностью. После этого в массив С переписывается «хвост» второго массива.
Рассмотренный алгоритм в худшем случае совершает m + n сравнений, где m и n – размеры сливаемых массивов. Поэтому его сложность по времени имеет оценку T(n, m) = O(m+n).
