Самостоятельная работа 3 Оценка риска на основе обработки экспертной информации

Задание. Имеется матрица результатов оценивания риска m альтернатив d экспертами. Разработать программный продукт для определения риска несогласованности экспертных оценок, если каждому объекту присвоен ранг по уровню риска каждым экспертом.

В исходных данных (табл.4) указан диапазон оценивания альтернатив. Необходимо с помощью генератора случайных чисел определить значение оценки каждого эксперта по каждой альтернативе.

Таблица 3 – Данные результатов оценки

Номер варианта	m	d	Диапазон оценивания
1	6	5	[1..6]
2	7	4	[1..7]
3	8	5	[1..8]
4	5	6	[1..12]
5	6	5	[1..10]
6	6	4	[1..6]
7	5	6	[1..5]
8	5	5	[1..7]
9	5	5	[1..5]
10	5	5	[1..12]
11	7	6	[1..12]
12	7	6	[1..6]
13	8	4	[1..6]
14	8	4	[1..5]
15	9	4	[1..5]
16	9	4	[1..10]
17	5	6	[1..7]
18	7	6	[1..5]
19	6	5	[1..10]
20	7	4	[1..12]
21	8	5	[1..10]
22	9	4	[1..8]
23	5	4	[1..5]
24	5	7	[1..6]
25	6	6	[1..5]

Краткие теоретические сведения Построение обобщенной оценки при обработке экспертами информации

Построение гипотезы о согласованности суждений экспертов. Выдвигается гипотеза H₀ о том, что эксперты являются достаточно точными измерителями, на основе подтверждения которой можно выявить возможные формулировки в экспертной группе. Степень согласованности экспертных оценок выражается посредством коэффициента согласования.

Постановка задачи

Имеется m объектов и d экспертов, построена матрица результатов ранжирования имеющихся объектов данными экспертами с элементами r_ij, где r_ij – ранг, присвоенный j-м экспертом I-му объекту. Необходимо определить степень согласованности экспертных оценок.

Алгоритм решения

1. Рассчитывается сумма ранга по каждому ряду:

, (13)

где r_i – реализация случайной величины.

2. Обозначим через V (вариация) изменение значений:

, (14)

где - оценка математических ожиданий.

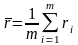(15)

3. Преобразуя перечисленные математические формулы и сократив на множитель m-1, получим следующую формулу:

. (16)

Эта формула определяет коэффициент согласования при отсутствии связанных рангов (одинаковых значений в одном столбце). При наличии связанных рангов коэффициент согласования определяется по формуле

, (17)

где T_j– это показатель связанных рангов в j-м ранжировании.

, (18)

где h_k– это число равных рангов в k-й группе связанных рангов при ранжировании j-м экспертом.

Если нет сходящихся рангов, то H_j=0, h_k=0, следовательно, T_j=0, и отношение (21) равняется соотношению (22).

W=1, если результаты ранжирования экспертов одинаковы, и W=0, если все результаты ранжирования экспертов различны. Для подтверждения гипотезы или опровержения гипотезы H₀ используем ²-критерий. Рассчитывается по формуле

. (19)

Если ²_{наблюдаемое}≥²_{норматив}, то гипотеза H₀ принимается. Если c²_{наблюдаемое}≤c²_{норматив}, то гипотеза H₀ отвергается.

c²_{теоретическое}=c²(α,a), где a – число степеней свободы, a=m-1; m – количество объектов, которые обследует эксперт; α – уровень значимости (0,01;0,05).