Изобарный процесс
Изобарным процессом называется процесс, протекающий при постоянном давлении.
1) р = const.
2
)
P
T
2
dS > 0
δq > 0
1
2
1
l
qp
V
S
Рис. 10
3) pV1 = RT1; pV2 = RT2.
Разделив почленно эти выражения, получим:
;
;
.
4) Изменение внутренней энергии и энтальпии
ΔU = U2 – U1 = Cv (T2 – T1);
Δi = i2 – i1 = Cp (T2 – T1).
5) Изменение энтропии и графическое изображение процесса в системе T, S координат, рис. 10
.
6) Работа изменения объема
.
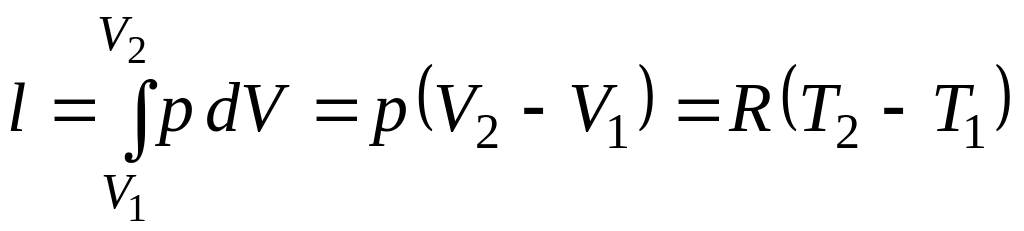7) Теплота процесса
δq = Cpm dT; q = Cpm (T2 – T1).
8) Аналитическое выражение I-го закона термодинамики.
Все подведенное к рабочему телу тепло расходуется на изменение внутренней энергии и работу изменения объема
δq = dU + δl; q = ΔU + l.
Из рассмотрения выражения I закона термодинамики получим:
q = ΔU + l
или
Cp (T2 – T1) = Cv (T2 – T1) + R (T2 – T1)
откуда
Cp = Cv + R; Cp – Cv = R.
Приведенное выражение называют уравнением Майера. Поясним уравнение Майера.
В изохорном процессе, согласно I закону термодинамики, тепло, подведенное к рабочему тела, расходуется только на изменение внутренней энергии, а в изобарном – на изменение внутренней энергии и работу, поэтому изобарная теплоемкость больше изохорной на величину работы. Напомним, что газовая постоянная представляет собой работу 1 кг рабочего тела в изобарном процессе при изменении температуры на 1 К
Изотермический процесс
Изотермическим процессом называется процесс, протекающий при постоянной температуре.
1) Т = const.
2)
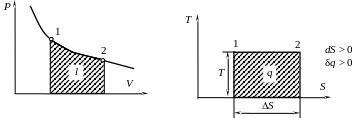
Рис. 11
В системе p, V координат изотерма представляет собой равнобокую гиперболу.
3) Из соотношения p1V1
= p2V2
= const получим:
.
4) Изменение внутренней энергии и энтальпии
dU = Cvm dT = 0; ΔU = U2 – U1= 0
di = Cpm dT = 0; Δi = i2 – i1 = 0.
Изменение внутренней энергии (идеального газа) не происходит
5) Изменение энтропии и изображение процесса в системе T, S координат, рис. 11.
.
6) Работа изменения объема
.
Подставим в подинтегральное
выражение значение
.
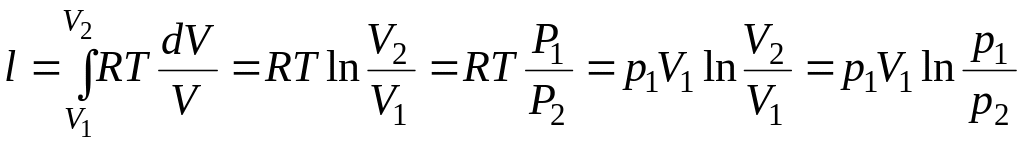7) Теплота процесса:
.
8) Аналитическое выражение I закона термодинамики.
Всё подведенное к рабочему телу тепло расходуется на работу изменения объема. δq = δl; q = l.
Адиабатный процесс
Процесс, протекающий без теплообмена с окружающей средой, называется адиабатным. В адиабатном процессе δq = 0; q = 0.
Получим уравнение адиабаты
Первый закон термодинамики
dU + δl = 0
Cv dT + p dV = 0. (13)
Продифференцируем характеристическое уравнение состояния
pdV + Vdp
= RdT, откуда dT
=
(pdV
+ Vdp).
Подставим значение dT в уравнение (13)
(pdV
+ Vdp) + pdV = 0.
Преобразуем приведенное выражение
;
.
;
.
Разделив переменные и проинтегрировав (14), получим:
;
;
.
;
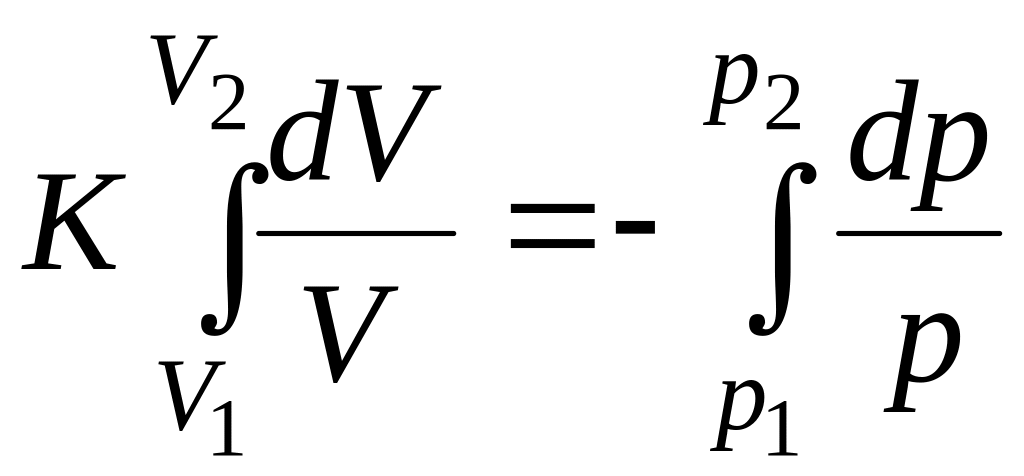откуда
или
.
. (15)
2
)
Рис. 12
3) Зависимость между параметрами состояния рабочего тела
;
.
;
.
;
;
;
.
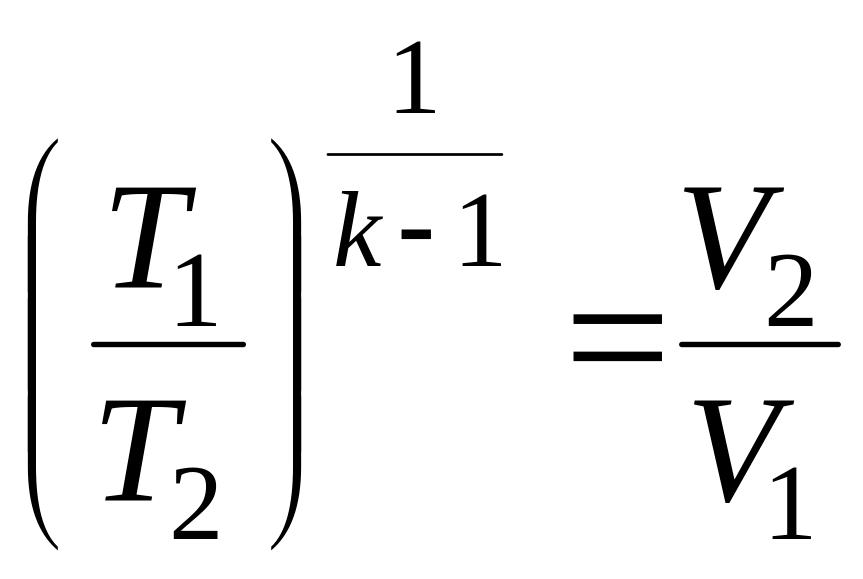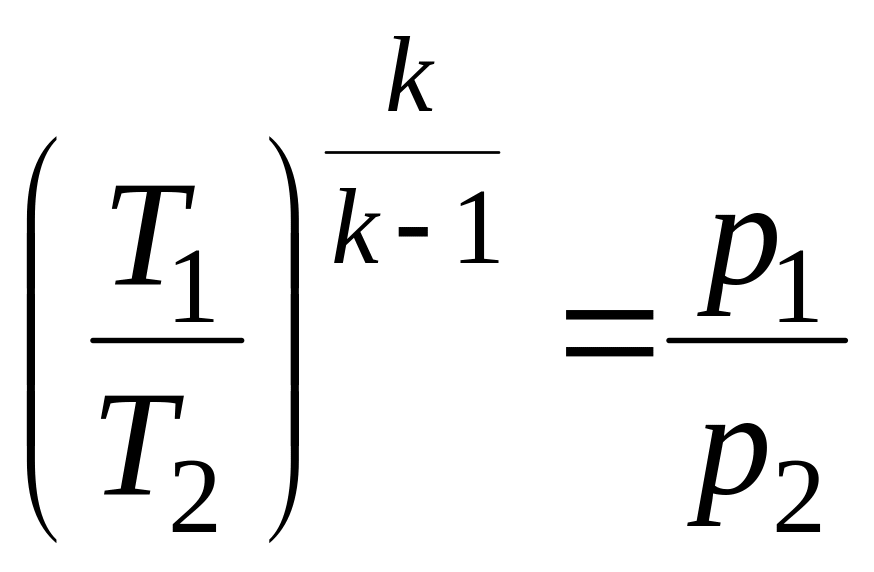4) Вычисление изменения внутренней энергии и энтальпии
ΔU = U2 – U1 = Cvm (T2 – T1).
Δi = i2 – i1 = Cpm (T2 – T1).
5) Изменение энтропии и изображение процесса в T-S координатах:
dS =
;
δq = 0; dS = 0; ΔS = S2
– S1 = 0.
В адиабатном обратимом процессе изменение энтропии не происходит. Поэтому адиабатный процесс называют изотропным.
6) Работа изменения объема
l =
.
7) Теплота процесса
δq = 0; q = 0.
8) Аналитическое выражение I закона термодинамики. Работа совершается за счет изменения внутренней энергии
l = –ΔU = U1 – U2.