Энтропия
В курсе математики показано, чтобы дифференциальный двучлен превратить в полный дифференциал некоторой функции, необходимо умножить его на интегрирующий множитель (делитель).
Для дифференциального уравнения I-го закона термодинамики
δq = Cv dT + p dV.
Интегрирующим делителем является абсолютная температура, тогда
.
,
. (11)
Выражение (11) является полным дифференциалом некоторой функции состояния рабочего тела dS, названной энтропией.
. (12)
Энтропия S есть функция состояния рабочего тела.
Отметим, что пари увеличении энтропии (dS > 0) тепло подводится к рабочему телу (δq > 0). При уменьшении энтропии (dS < 0) тепло отводится (δq < 0). В термодинамических расчетах пользуются величиной изменения энтропии.
Вычислить изменение энтропии в термодинамическом процессе можно путем интегрирования выражения:
.
.
|
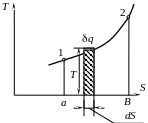
Рис. 8 |
T-S диаграмма
Можно использовать энтропию совместно с абсолютной температурой для изображения различных термодинамических процессов, используя выражение (12). δq = T dS – представляет собой элементарное тепло, участвующее в процессе. Тогда полное количество тепло можно представить в виде
пл.
12 ва.
Тепло, участвующее в процессе в системе T, S – координат может быть представлено в виде площади, ограниченной кривой процесса, крайними ординатами и осью абсцисс.
Анализ основных термодинамических процессов с идеальными газами
Задачей анализа термодинамических процессов является установление закономерностей изменения параметров состояния рабочего тела и принципа распределения энергии в соответствии с I законом термодинамики. Практический интерес представляет исследование следующих процессов:
1. Изохорного, протекающего при постоянном объеме V = const.
2. Изобарного, протекающего при постоянном давлении р = const.
3. Изотермического, протекающего при постоянной температуре Т = const
4. Адиабатного, протекающего без теплообмена с окружающей средой δq = 0, q = 0.
5. Политропного, протекающего при постоянной теплоемкости.
Анализ процессов проводится в следующем порядке:
1. Записывается уравнение процесса из условий его протекания.
2. Приводится графическое изображение процесса в системе p, V и T, S координат.
3. Устанавливается зависимость между параметрами состояния рабочего тела в начале и в конце процесса.
p = f(v); p = f(T); T = f(V).
4. Вычисляются изменения внутренней энергии и энтальпии
dU = CvdT, ΔU = U2 – U1 = Cv (T2 – T1), Δi = i2 – i1 = Cp(T2 – T1).
5. Вычисляется изменение энтропии и приводится графическое изображение процесса в системе T, S координат.
,
.
6. Вычисляется работа изменения объема
;
.
7. Вычисляется количество тепла, участвующее в процессе
;
.
8. Аналитическое выражение I закона термодинамики.
Изохорные процесс
1) Изохорным процессом называется процесс, протекающей при постоянной объеме V = const.
2
)
P
T
2
2
dS > 0
δq > 0
1
1
qv
V
S
b
a
Рис. 9
3) Запишем характеристические уравнения состояния для начального и конечного состояний, разделим их друг на друга
;
откуда
;
.
4) Изменение внутренней энергии и энтальпии
ΔU = U2 – U1 = Cv (T2 – T1); Δi = i2 – i1 = Cp (T2 – T1).
5) Изменение энтропии
.
6) Работа изменения объема
.
Работа изменения объема в изохорном процессе не производится (l = 0).
7) Теплота процесса:
.
в T, S координатах теплота qv представлена площадью 1-2-а-в.
8) I закон термодинамики
Тепло, подведенное к рабочему телу, расходуется на изменение внутренней энергии δq = dU; q = ΔU.