6 Синтез кулачкового механизма
6.1 Исходные данные
Схема кулачкового механизма изображена на рисунке 6.1 , а на рисунке 6.2 – диаграмма параболического закона изменения аналога ускорения толкателя .
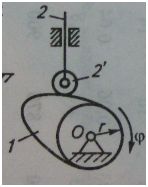
Рисунок 6.1 – Схема кулачкового механизма
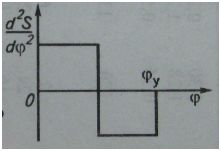
Рисунок 6.2 –Закон изменения второй передаточной функции
Фазовые углы: 
;
;
максимальный ход толкателя 
.
6.2 Аналитические выражения второй и первой передаточных функций и функции положения
6.2.1 На первом
участке(
):
,
(6.1)
где a – амплитуда.
Проинтегрировав, получим:
;
(6.2)
Проинтегрировав ещё раз, получим:
;
(6.3)
Постоянные
интегрирования 
и 
определяем по начальным значениям
функций 
и 
при 
.
В этой точке скорость 
и следовательно 
.
В результате получим 
и выражения 6.1, 6.2, 6.3 приобретают вид
системы:
(6.4)
6.2.2 На втором
участке (
):
,
(6.5)
Проинтегрировав,
получим:
;
(6.6)
Проинтегрировав ещё раз, получим:
;
(6.7)
Постоянные
интегрирования определяем при 
из условий
и 
.
Используя второе
и третье уравнение системы 6.4 запишем
для 
;
; 
;
(6.8)
А для начала второго участка используем выражения 6.6 и 6.7:
;
;
(6.9)
Приравняв правые части выражений 6.8 и 6.9 получим:
и 
;
При 
.
Подставив
,
,
в выражение 6.9 и приравняв к 
мм
Подставив все значения в выражения 6.4, 6.6 и 6.7 , получим :
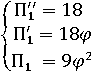
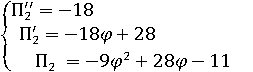(6.10)
Третий и четвёртый участок (фаза возвращения) симметричны первым двум.
6.3 Расчёт и построение графиков второй и первой передаточных функций положения толкателя.
6.3.1 Значение функций
,
, 
определим для 8 положений кулачка в
фазах подъёма и возвращения. Для фазы
подъёма угловой шаг равен:
(6.11)
Для фазы возвращения:
(6.12)
Расчёт значений функций производим по формулам (6.10).
Результаты расчётов вводим в таблицу 6.1
Таблица 6.1 – Результаты расчётов
-
Фаза
№ положения
φ
φ
Участок
рад.
град.
мм
мм
мм
Подъём
0
0
0
1
18
0
0
1
0,196
11,25
1
18
3,5
0,35
2
0,392
22,5
1
18
7
1,38
3
0,589
33,75
1
18
10,5
3,12
4
0,785
45
1/2
18/-18
14
5,5
5
0,981
56,25
2
-18
10,5
7,81
6
1,178
67,5
2
-18
7
9,5
7
1,373
78,75
2
-18
3,5
10,48
8
1,57
90
2
-18
0
11
Возвращение
9
2,618
150
2
-18
0
11
10
2,814
161,25
2
-18
-3,5
10,48
11
3,01
172,5
2
-18
-7
9,5
12
3,206
183,75
2
-18
-10,5
7,81
13
3,402
195
2/1
-18/18
-14
5,5
14
3,598
206,25
1
18
-10,5
3,12
15
3,794
217,5
1
18
-7
1,38
16
3,99
228,75
1
18
-3,5
0,35
17
4,186
240
1
18
0
0
6.3.2 Далее определим масштабные коэффициенты при осях координат.
По оси абсцисс:
K=
,
(6.13)
где 
– отрезок оси абсцисс, изображающий
фазовый угол 
.
Для графика :
KП” = |П''max|/a = 18 / 54= 0,33 мм /мм, (6.14)
где |П''max| – максимальная по оси абсцисс величина значения из таблицы 6.1, а = 54 – соответствующее масштабное значение этой величины.
Аналогично определяем:
KП’ = |П'max|/b = 14/56 = 0,25 мм/мм (6.15)
KП = |Пmax|/c = 11/44 = 0,25 мм/мм (6.16)