2.3 Построение планов ускорений

2.3.1 Планом ускорений называют рисунок, на котором в масштабе изображены векторы, равные по модулю и направлению ускорениям различных точек звеньев механизма в данный момент времени.

Построение планов ускорений покажем на примере положения механизма № 1.

Планы ускорений механизма строим для положений механизма 0,1,7,10.

Полагая, что ₁ = const, определим ускорение точки А звена 2.

Ускорение точки А кривошипа 1 и ползуна 2 при постоянном :

(2.13)

На чертеже строим вектор = мм;

Произведем расчёт масштабного коэффициента :

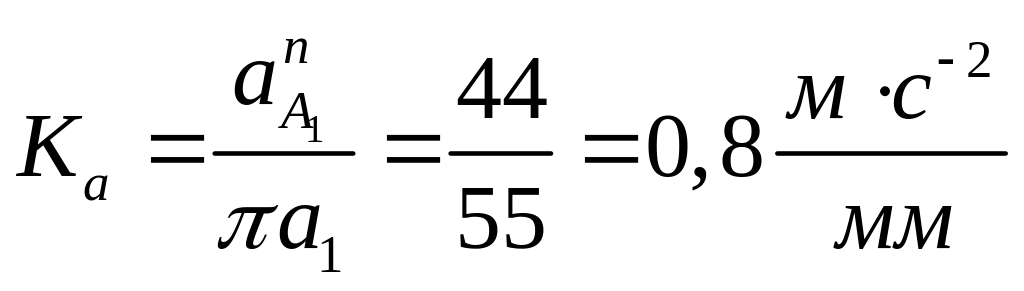(2.14)

Аналогично предыдущему пункту для построения планов ускорений нам понадобятся системы векторных уравнений ускорений

Ускорение точки кулисы 3 находим, используя векторные уравнения:

(2.15)

В этих уравнениях – ускорение Кориолиса. Чтобы опреде­лить его направление, поворачиваем вектор относительной скорости на угол 90º в сторону вращения кулисы. Откладываем от точки вектор , длина, мм, которого , и в точке k восстанавливаем перпендикуляр – линию дейст­вия касательного ускорения (направлен вдоль AC).

Ускорение точки C равно нулю; нормальное ускорение при вращении ку­лисы и направлено параллельно АC.

Длина, мм, вектора . В конце вектора восстанавливаем

перпендикуляр к нему – линию действия касательного ускорения до пересечения её с ранее проведенной ли­нией действия ускорения Полученную точку соединяем с полюсом . Из плана ускорений находим

; (2.16)

(2.17)

Ускорение точки ползуна 4 находим, используя векторные уравнения :

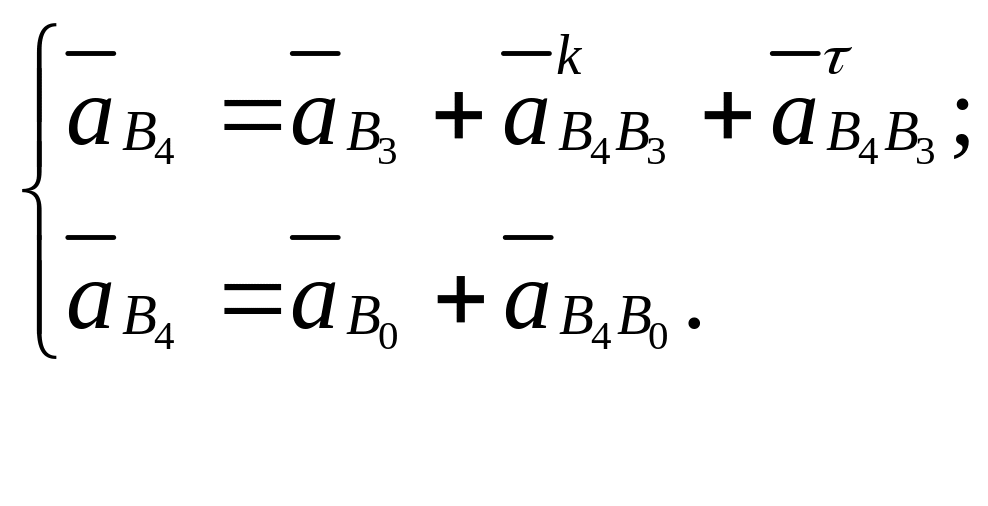(2.18)

В этих уравнениях – ускорение Кориолиса. Чтобы опреде­лить его направление, поворачиваем вектор относительной скорости на угол 90º в сторону вращения кулисы. Откладываем от точки вектор , длина, мм, которого . Вектор касательного ускорения направлен параллельно оси BC кулисы.

4.3.2 Расчёт на примере 1-го положения ускорений Кориолиса и нормального ускорения:

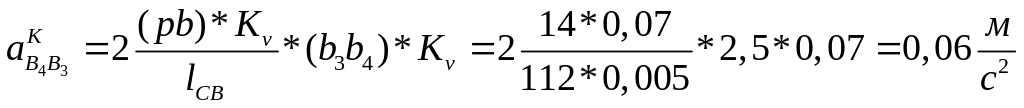
Занесем полученные данные в таблицу результатов 2.2

Таблица 2.2 – ускорения ( )

№ пол.
0	44	44	21,6	21,6	20,4	0	0	0	4,8
1	44	57,6	23,6	28,8	30	10,4	54,4	0,8	11,6
7	44	40	13,2	14,4	15,6	12	28,8	0,8	0,4
10	44	32,8	10,8	12	12,8	8	31,2	1,2	1,2

2.4 Построение графиков функции положения и передаточных функций выходного звена.

2.4.1. Построение графика функции положения выходного звена проводится с использованием планов положений механизма.

Выбираем масштабный коэффициент по оси ординат графика:

K_S = K_l /2; (2.19)

K_S = 0,0025 м/мм.

Выбираем масштабный коэффициент по оси абсцисс графика:

K_φ = (2 ) / L; (2.20)

K_φ = (2 · 3,14) / 240 = 0,026 рад/ мм .

Отрезок на оси абсцисс делим на 12 равных частей. На оси ординат откладываем отрезки, равные удвоенным расстояниям с планов механизма. Соединяем полученные точки лекальной кривой и получаем диаграмму перемещений пуансона 5 (точки B).

Диаграмма скоростей пуансона получена графическим дифференцированием диаграммы перемещения с использованием метода хорд. При этом масштабный коэффициент по оси ординат полученного графика выражается следующей формулой:

; (2.21)

Масштабный коэффициент по оси абсцисс графика остается K_φ.

Диаграмма ускорений пуансона получена графическим дифференцированием диаграммы скоростей с использованием метода хорд. При этом масштабный коэффициент по оси ординат полученного графика выражается следующей формулой:

; (2.22)