3 Разработка функциональной схемы программного продукта
Функциональная схема программного продукта представлена на рисунке 8.
Рисунок 8 – Функциональная схема программного продукта
4 Проектирование классов предметной области
4.1 Построение диаграммы классов
Class diagram (диаграмма классов) — основная диаграмма для создания кода приложения. При помощи диаграммы классов создается внутренняя структура системы, описывается наследование и взаимное положение классов друг относительно друга. Здесь описывается логическое представление системы. Именно логическое, так как классы — это лишь заготовки, на основе которых затем будут определены физические объекты.
Диаграмма классов представлена на рисунке 9.
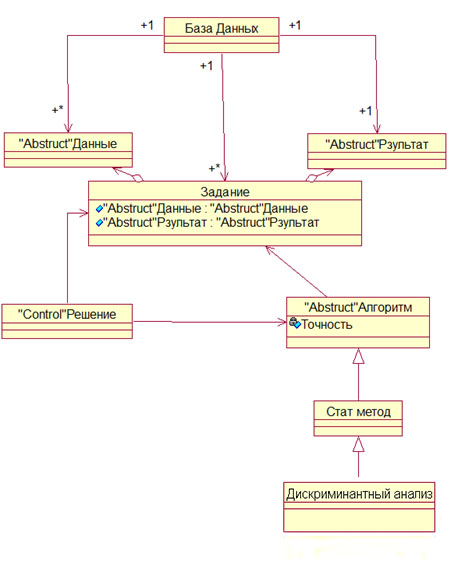
Рисунок 9 - Диаграмма классов
4.2 Уточнение структуры классов предметной области и разработка алгоритмов методов
Для реализации математического аппарата разрабатываемой АИС был выбран корреляционно-регрессионный анализ. Алгоритм данного метода представлен в виде диаграммы состояний изображенной на рисунке 10.
Основные этапы алгоритма:
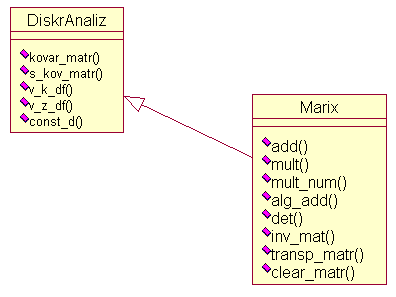
Рисунок 10 - Уточненная структура класса «Регрессионный анализ»
Описание функций класса «Регрессионный анализ» приведено в таблице 5.
Таблица 5 - Описание функций класса «DiskrAnaliz»
Название функции |
Описание |
Kover_matr() |
Вычисление коваариционной матрицы |
S_kover_matr() |
Вычисление функции S коваариционной матрицы |
v_k_df() |
Вычисление вектора дисритизации |
v_z_df() |
Вычисление значение дискриминантной функции |
Const_d() |
Вычисление константы дисритизации |
Таблица 6 - Описание функций класса «Matrix»
Название функции |
Описание |
add() |
Добавленеие матрицы |
mult() |
Умножене матриц |
Mult_num() |
Умножене матриц на число |
Alg_add() |
Добавление среднего значения |
det() |
Вычисление детерминанта |
Inv_mat() |
Инвентирование матриц |
Transp_matr() |
Транспонирование матриц |
Clear_matr() |
Очистка матрицы |
5 Выбор стратегии тестирования и разработка тестов
Тестирование программного средства осуществляется с цель проверки правильности функционирования разработанного программного кода.
Тестирование проведено на основе контрольного набора данных согласно условиям решаемой задачи.
Таблица 2 – Исходные данные
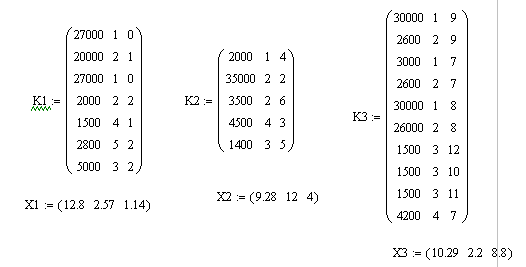
Здесь:
– стоимость тыс. р.;
–тип техники,
шт.;
–срок службы,
дни, K-отделы,
X1,X2,X3-средние
значения переменных.
Решение. Для каждой группы предприятий рассчитаем ковариационные матрицы.
.
Первая
группа (
)
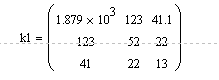
Вторая
группа (
):
Третья
группа (
):
Для каждой из существующих пар подмножеств рассчитаем совместные ковариационные матрицы и матрицы, обратные к ним.
Совместная
ковариационная матрица и обратная к
ней матрица для первого и второго
подмножеств и
разность векторов средних величин
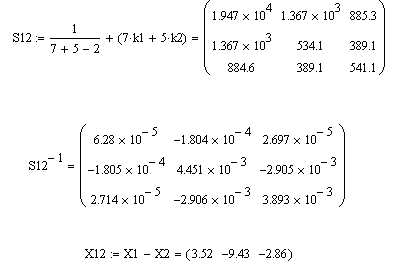
Совместная
ковариационная матрица и обратная к
ней матрица для первого и третьего
подмножеств и
разность векторов средних величин
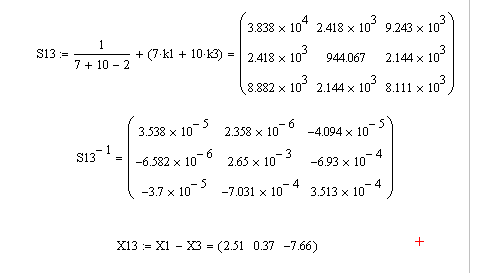
Наконец,
совместная ковариационная матрица и
обратная к ней матрица для второго и
третьего подмножеств и
разность векторов средних величин
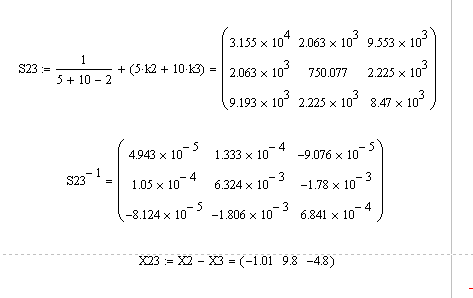
На
основании обратных матриц
,
,
и разностей векторов средних значений
определим для каждой пары подмножеств
векторы коэффициентов дискриминантных
функций:
Определяем значения дискриминантных функций по матрице значений исходных переменных в каждом подмножестве.
Для разграничения первого и второго подмножеств и подмножеств константа дискриминации равна:
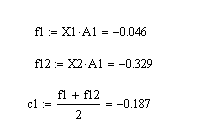
Для разграничения первого и третьего подмножеств и подмножеств константа дискриминации равна:
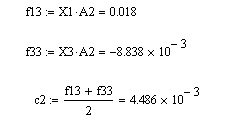
Для разграничения второго и третьего подмножеств и подмножеств константа дискриминации равна:
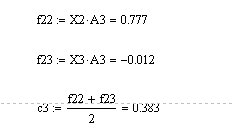
В общем виде дискриминантные функции для трех подмножеств имеют вид:
Следовательно, границы трех классов будут определяться системой уравнений
Чтобы начать классификацию новых объектов, подставим значения исходных переменных в выражение и сравним полученные результаты с нулем,
если
и
,
то объект принадлежит первому множеству;
и
,
то объект принадлежит второму множеству;
и
,
то объект принадлежит третьему множеству.
Для модели Slereo X4: X1=2700 X2=1 X3=0
и объект принадлежит второму множеству.
Результат: Наиболее подходящий отдел № 2.
Программная реализация контрольного примера представлена в виде экранной формы на рисунках 11-13.
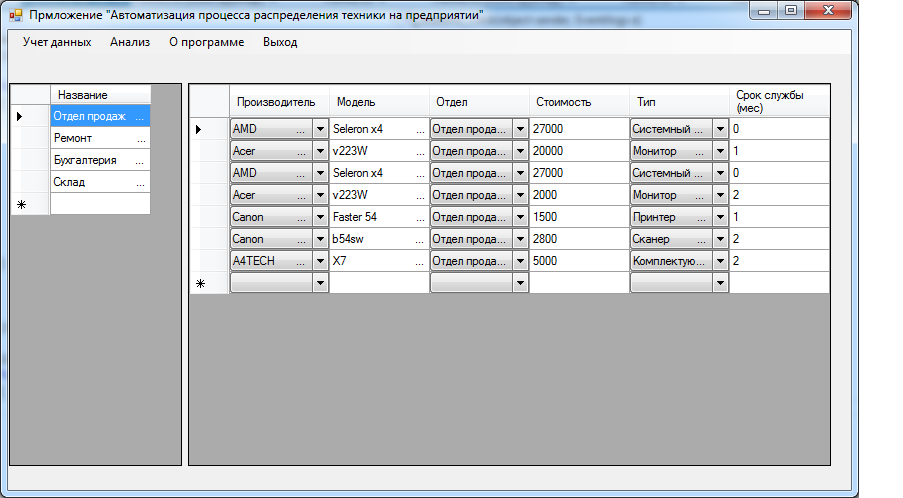
Рисунок 11 – Форма с исходными данными
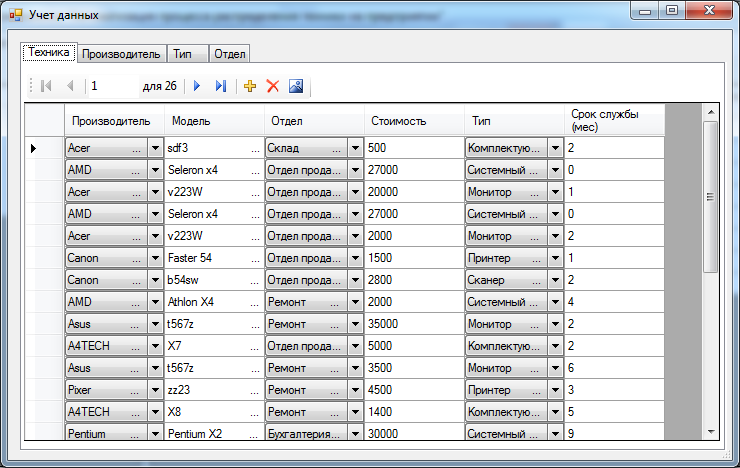
Рисунок 12 – Форма Учета Данных
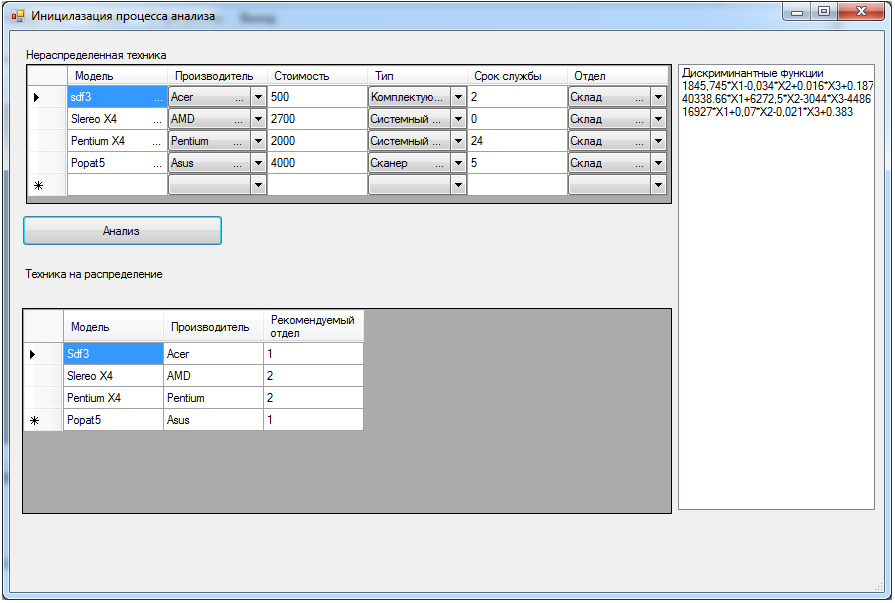
Рисунок 13 – Форма с Анализа
Вывод: Расчетные значения совпадают со значениями с допустимой погрешностью , полученными при решении программным средством.