Задачи 21 – 30

• Для заданного сечения, составленного из простых геометрических фигур, определить положение центра тяжести.

К решению этих задач следует приступать после изучения темы «Центр тяжести». С целью упрощения решения следует:

• разбить заданное сложное сечение на минимальное количество простых фигур, центры тяжести которых известны;

• рационально выбрать оси координат;

• показать положение центра тяжести каждого простого сечения;

• определить положение каждого центра тяжести относительно выбранных осей;

• определить центр тяжести всего сложного сечения.

41

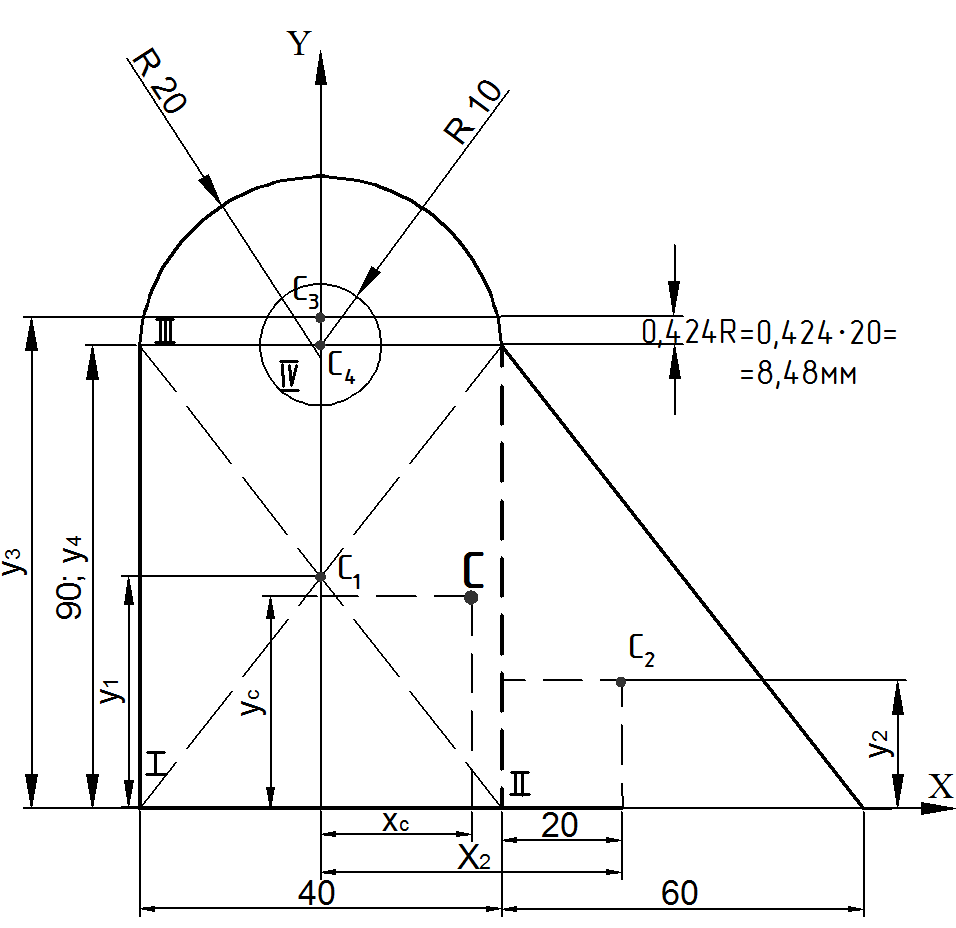
Дано: сложное сечение, состоящее из простых геометрических фигур.

Определить: Χ_с ; У_с

Решение:

1. Сложное сечение разбиваем на минимальное количество простых, центры тяжести которых известны: I, II, III, IV;

2. Определяем и показываем центры тяжести каждого простого сечения: С₁, С₂, С₃, С₄;

3. Рационально выбираем оси координат Χ и У;

4. Определяем положение каждого центра тяжести относительно выбранных осей:

Χ1 = 0;	У1 =
Χ2 =	У2 =
Χ3 = 0	У3 = 90 + 8,48 = 98,48 мм = 9, 85 см;
Χ4 = 0.	У4 = 90 мм = 9 см.

5. Определяем площади простых геометрических фигур:

А₁ = 40·90 =3600 мм² = 36 см²

А₂ = ;

А₃ = ;

А₄ = πR² = 3,14 · 10² = 314 мм² = 3,14 см².

6. Определяем координаты центра тяжести всей сложной фигуры:

Χ_с = =

1,63 см =

У_с =

42

4,18 см =

Ответ: Χ_с = 16,3 мм; У_с = 41,8 мм.

43

Задачи 31-40

• Для заданного стального бруса определить значения моментов М_АВ, М_ВС, М_СД; построить эпюры крутящих моментов.

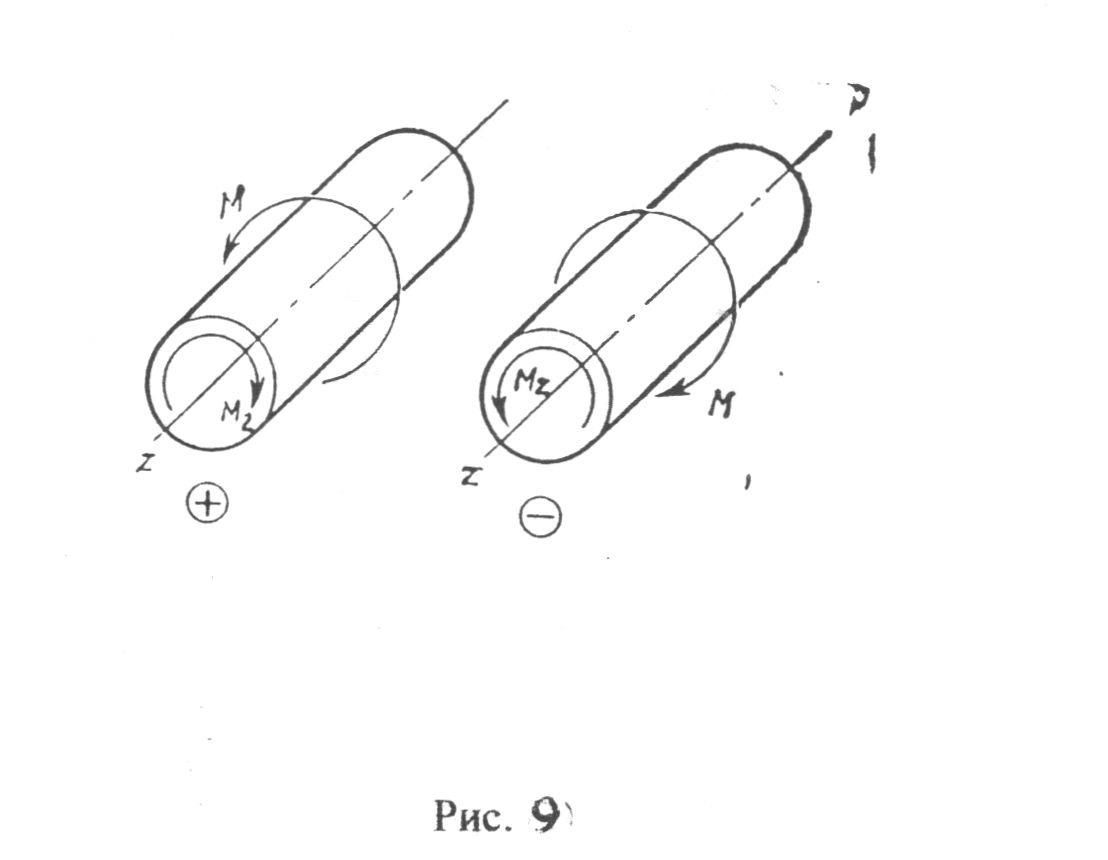Кручением называют такой вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – крутящий момент М_кр (М_z). Крутящий момент в произвольном поперечном сечении бруса равен алгебраической сумме внешних моментов, действующих по одну сторону от сечения

Имеется в виду, что плоскости действия всех внешних моментов М_кр перпендикулярны продольной оси бруса.

Будем считать крутящий момент положительным, если для наблюдателя, смотрящего на проведенное сечение, он представляется проведенным по часовой стрелке. Соответствующий внешний момент направлен против часовой стрелки.

Дано:

Р₁ = 9 кВт;

Р₂ = 15 кВт;

Р₃ =3 кВт;

ω = 10 рад/с.

Определить: М₁; М₂; М_3.

Решение:

1. Определяем значения моментов М₁, М₂, М₃:

М ₁ = = 900 Н·м;

М ₂ = = = 1500 Н·м;

М ₃ = = = 300 Н·м.

2. Строим эпюру крутящих моментов, применяя метод сечения. Проводя мысленно сечение в пределах каждого из участков, идя от свободного конца,

будем отбрасывать закрепленную часть бруса и оставлять для рассмотрения незакрепленную:

44

М_{кр АВ} = М_АВ = 900 Н·м;

М_{кр ВС} = М_АВ+М_ВС = -900 + 1500 = 600 Н·м;

М_{кр СД} = М_АВ+М_ВС+М_СД = -900+1500-300 = 300 Н·м.

Ответ: М_{кр АВ} = 900 Н·м; М_{кр ВС} = 600 Н·м; М_{кр СД} = 300 Н·м.

М₁ м₂ м₃

45