Раздел 2. Задачи на нормальное распределение

Даже, несмотря на анализ данных, который я провожу, и выводы, которые уже можно сделать, родители всегда будут до последнего сомневаться в правильности выбора школы для своего ребёнка. Я думаю, вы согласитесь, что помимо зависимостей есть ещё человеческий фактор, случайность и вообще много чего ещё.

Сейчас я постараюсь ещё немного помочь и приблизить родителей к заветной цели-выбору школы. Для этого мы будем исследовать вероятность событий, которые, по моему мнению, очень важны и дополняют сложившуюся уже картину.

Исследование мы будем проводить при помощи Excel и функции “НОРМРАСП», так как именно она ищет вероятность по значению.

Для примера возьмём один из старейших вузов, входящий в 200 лучших институтов мира - Санкт-Петербургский государственный университет (СПбГУ).

Выясним вероятность того, что случайно выбранный школьник, сдающий ЕГЭ по русскому языку получит более 72 баллов (7). Это значение в 2014 году будет минимальным проходным для поступления на бюджет в СПбГУ по данной дисциплине

Для этого нам понадобиться среднее, стандартное отклонение, интегральная.

(1-НОРМРАСП(72;67,02;5,766;1))*100%=19,38% (7)

Итак, получается, что вероятность того, что случайно выбранный школьник за ЕГЭ по русскому языку получит более 72 баллов и получит шанс поступить в СПбГУ, равняется 19,38 процента.

То же самое выясним касательно математики. Этот предмет, пожалуй, ещё важнее. Ведь русский большинство из нас знает с детства и нам легче его сдать априори. А вот точные науки, такие математика как всегда более сложны и требовательны к знаниям.

И так, выясним, какова вероятность того, что случайно выбранный школьник, сдающий ЕГЭ по математике получит более 62 баллов (8). Это значение по аналогии с русским языком в 2014 году будет минимальным проходным для поступления на бюджет по данной дисциплине.

Средний балл по такому сложному предмету – это уже не плохо, но не гарантирует поступления в более престижные вузы. Поэтому так важно узнать вероятность данного события.

(1-НОРМРАСП(64;51,786;8,61;1))*100%= 7,8% (8)

Таким образом я выяснил, что вероятность того, что случайно выбранный школьник за ЕГЭ по математике получит более 62 баллов и будет иметь шанс поступить в СПбГУ , ровняется 7,8 процента

Раздел 3. Различные виды анализа

Получив первое представление об исследуемых школах, нам важно продолжать двигаться дальше. Для работы мы будем использовать различные виды анализа: такие как кластерный, корреляционный, дисперсионный и регрессионный.

3.1. Кластерный анализ

Кластерный анализ нужен нам для того, чтобы упорядочить наш объект исследований в сравнительно однородные группы, для лучшего понимания данных и выделения нетипичных объектов.

Я разделю наши школы на направления и проанализирую полученную информацию (приложение №3).

В процессе кластеризации школы были разделены на 4 группы.

В первую группу вошли 4 школы, у которых средний балл за ЕГЭ по русскому самый высокий, а занятия начинаются в 8:30 утра. Это школы: № 148, №98, №95 и № 184.

Во вторую группу вошла 1 школа. Мы на эту школу уже обращали внимание-это учебное заведение №55.Она и основана была не так давно - в 1955 году и у неё самый худший показатель по русскому и один из худших по математике. Я так понимаю - это школа для отстающих детей.

В третью группу вошли так называемые школы «среднечки». Средний балл у них ниже всех по сравнению с другими. Хотя и тут выделяются несколько школ. Школы с уровнем баллов выше среднего по группе: Это школа № 72 и № 121.

Ну и в 4 вошли все остальные школы. На мой взгляд - это самая сбалансированная группа. Минимальный результат больше 70 баллов и больше половины школ из этой группы имеют результат выше 72.

В подтверждение выше сказанного построим график, в нашем случае лучше Boxplot. Мы взяли именно его, так как нас интересует динамика изменения одного признака по нескольким категориям.

В качестве переменной – ЕГЭ по русскому языку (средний балл) категория – кластеры (рис.11).

Рисунок 11

Построим ещё 1 график. Только теперь в качестве переменной будет выступать результат сдачи ЕГЭ по математике (рис. 12).

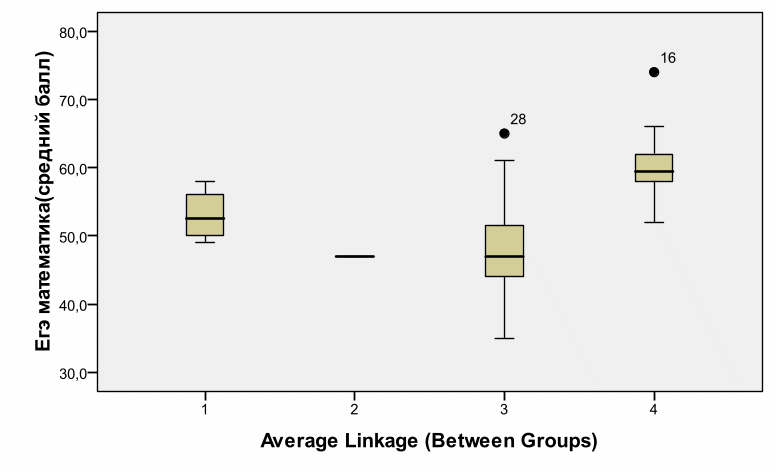
Рисунок 12

Начнём с 1 группы. Это те школы, у которой занятия начинаются в 8.30 и результаты ЕГЭ по русскому лучше всех. С математикой не всё так хорошо. Мне кажется, они в большей степени относятся к гуманитариям.

Группа 2 и школа № 55. Мы видим, что математика написана слабо, но не хуже всех школ в районе. Есть результаты намного хуже. И если бы не русский язык - она спокойно могла бы перейти в другой кластер. Видимо не хватает в этой школе хороших педагогов по русскому языку.

Группа 3. Как и по русскому языку, результаты достаточно сильно колеблются. Сюда вошли школы, как с наихудшими показателями, так и с наилучшими. Из общего числа выделяется школа № 146.

И наконец, группа 4. ЕГЭ по математике написано на достаточно хорошем уровне. Портит немного статистику Гимназия №192 со средним результатом в 52 балла. А выделяется школа №470 и не удивительно, ведь данная школа считается одной из сильнейших по математике в городе Санкт- Петербург.