6. Довжина вектора . Напрямні косинуси вектора .
Поділ відрізка в даному відношенні
Якщо
початок вектора
=
співпадає з початком координат точкою
О
, то довжина вектора
дорівнює
=
=
,
де х,у,z – координати вектора .
Якщо початок вектора = міститься в точці А ( х1 , y1, z1 ) , а кінець – в точці В ( х2 , y2 , z2 ) , то прох = ах = х2 – х1 , проу = ау = y2 - y1 ;
проz = az = z2 – z1 , тобто = ( х2 – х1, y2 - y1 , z2 – z1 ).
Тоді довжина вектора = дорівнює
=
=
Ця ж формула використовується для знаходження відстані між двома точками А і В .
О
значення
. Кутом між
вектором і віссю називається найменший
кут , на який треба повернути вектор ,
щоб його напрям збігся з додатним
напрямом осі.
z
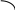γ
β
о
α у
х
Позначимо куб між вектором і віссю Ох через α , між і Оу – через β,
між і Оz – через γ :
,
= β
; (
) = γ
О скільки прох = ах = cos, проу = ау = cos β , проz = az = cos γ , то
c
os
=
; cos
β
=
cos
γ =
Означення . Косинуси кутів між вектором і осями координат називаються напрямними косинусами вектора .
З формул для обчислення напрямних косинусів випливає :
cos2+
cos2
+ cos2
γ =
=
=
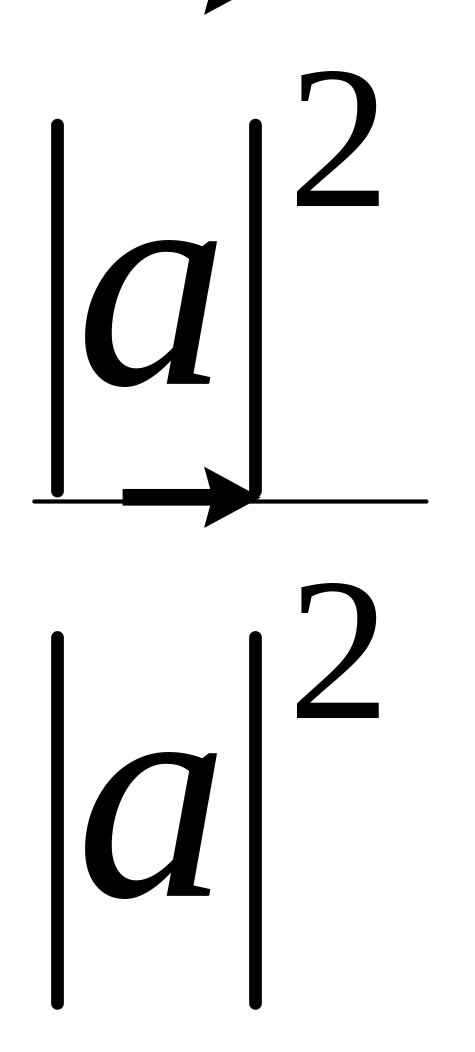1,
тобто суми квадратів напрямних косинусів довільного вектора дорівнює одиниці .
7. Скалярний добуток двох векторів, його властивості
Означення: Кутом φ між двома векторами і називається найменший кут на який потрібно повернути один з векторів, щоб його напрямок збігся з напрямком іншого вектора.
φ
Означення: Скалярним добутком двох векторів і називається число ,що позначається . , яке дорівнює добутку довжин цих векторів на косинус кута між ними.
Якщо хоча б один з векторів і нульовий то їх скалярний добуток дорівнює нулю: . =0.
Зауваження : Не існує скалярних добутків трьох і більшої кількості векторів
Оскільки
, а
,
то
;
В цьому полягає геометричний зміст скалярного добутку: скалярний добуток двох векторів дорівнює добутку одного вектора на проекцію на нього іншого вектора.
Нехай
тепер вектор
зображає переміщення
матеріальної точки, а вектор
-
сталу силу, що діє на переміщення
під
кутом φ.
φ
Роботою сили на переміщення називається скалярна величина А, що дорівнює скалярному добутку вектора сили на вектор переміщення.
А= · В цьому полягає механічний зміст скалярного добутку векторів.
Властивості скалярного добутку векторів
Алгебраїчні:
1.
-
комутативність скалярного добутку
2.
-
асоціативність відносно множення на
число
3.
дистрибутивність
відносно додавання векторів
Геометричні:
4.
Якщо
і
, то
,
коли кут
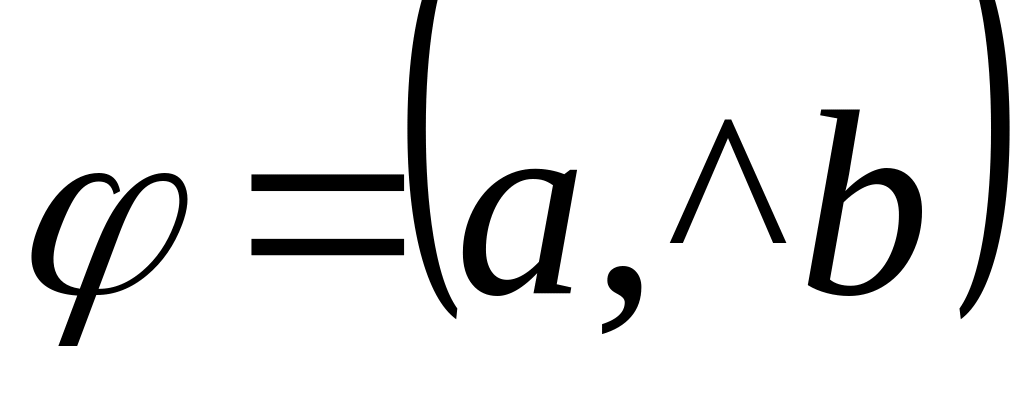гострий і
,
коли
- тупий.
5. Скалярний добуток двох ненульових векторів дорівнює нулю тоді і тільки тоді, коли ці вектори взаємно перпендикулярні :
6. Якщо вектори і колінеарні, то
+,
якщо
і
мають
один напрямок
-, якщо протилежний
Зокрема
,
тобто
скалярний квадрат вектора дорівнює
квадрату його довжини.
З останньої рівності
=
Скалярний добуток в координатній формі .
Нехай
вектори
і
задані
координатами в ПДСК :
= ах
ау
=(
ах,ау,аz
),
=
bх
bу
b
=(
bх,bу,bz
), власт. 3
Знайдемо їх скалярний добуток :
.
=
(
ах
ау
).
(
bх
bу
b
)
=ахbх
+
ахbу
+
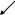
власт.1,5,6
Отже , скалярний добуток двох векторів , заданих координатами в ПДСК ,дорівнює сумі
добутків їх відповідних координат :
.
=
-
скалярний добуток в коорд.формі
За властивістю 6 довжина вектора
Цю ж формулу ми отримали в попередньому питанні іншим способом .
З означення скалярного добутку кут між векторами і визначається рівністю
соs
=
- відношення скал. добутку до добутку
довжин ,
або у координатній формі
соs
=
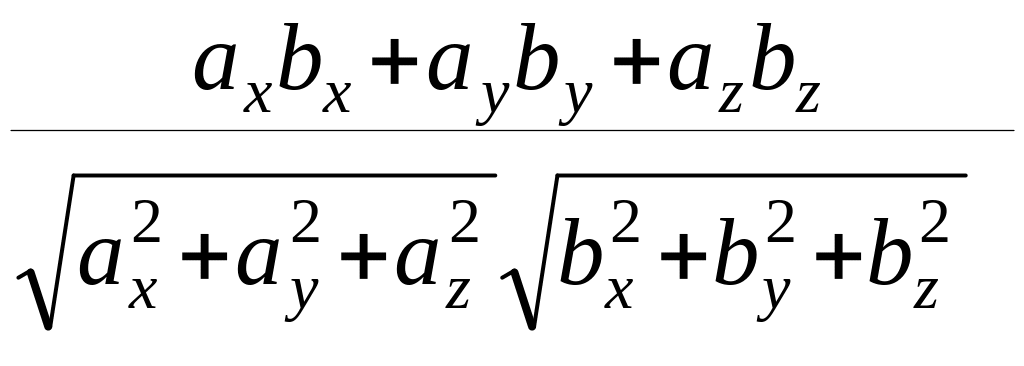
Приклад1. Відомо ,що
=
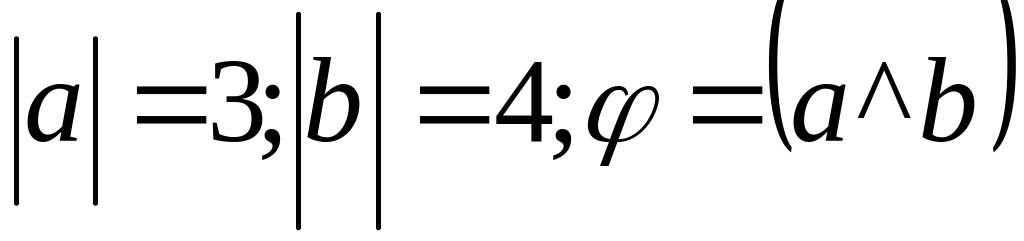Обчислимо
1
)
.
=
соs
= 3. 4
( -
)
= - 6 .
2)
3)
2.Знайти кут між діагоналями паралелограма , побудованого на векторах
соs
=
