Розкладемо вектор за базисом 1 2 3 :

= х_{1 1} + х_{2 2} + х_{3 3} ,

або в кординатному вигляді :

( 11 ; -6 ; 5 ) = ( 3 ; -2 ; 1 ) Х₁ + ( -1 ; 1 ; -2 )Х₂ + ( 2; 1 ; -3 )Х₃

В ектори рівні , коли їх відповідні координати рівні . Тому одержимо систему :

3 х₁ – х₂ + 2х₃ =11 3 -1 2 11 1 -2 -3 5

-2х₁ + х₂ + х₃ = -6 -2 1 1 -6 ~ 0 5 11 –4 ~

х₁ – 2х₂ – 3х₃ = 5 1 -2 -3 5 0 3 5 -4

1 -2 -3 5 1 0 0 2 х₁= 2, Отже ,

~ 0 1 - ~ 0 1 0 -3  х₂ =-3, = 2 ₁ - 3 ₂ + ₃

0 0 1 1 х₃ = 1 = ( 2; -3 ; 1 )

0 0 -

5. Координати точок і векторів в прямокутній декартовій системі координат.

У просторі геометричних векторів як базис можуть бути узяті будь-які 3 некомпланарні вектори. Якщо їх співвіднести до загального початку- точки 0 і розглянути сукупність точки 0 і базису, то матимемо декартову систему координат в просторі.

Зауваження: Декартові система координат названа на честь французького математика Рене Декарта.

Декартових систем координат існує стільки, скільки існує трійок не компланарних векторів. Серед множини систем координат виділяють прямокутну декартову систему координат (ПДСК), яка широко використовується.

Як базис у прямокутній ДСК берться упорядкована трійка попарно ортогональних одиничних векторів, яка позначається ( , ).

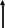
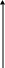
Означення: Базис називається ортонормованим.

Z

Y

0

X

Означення: Декартові система координат, базис якої ортонормований, називається прямокутною ДСК. (ПДСК). Точка 0- початок координат. Осі, що проходять через початок координат в напрямку базисних векторів – осі координат. Вісь, напрямлена як вектор називається віссю абсцис позначається Ох. Вісь, напрямлена як вектор називається вісю ординат позначається Оу. Вісь, напрямлена як вектор називається віссю аплікат позначається Oz.

Означення: Площини які проходять через осі координат, називаються координатними площинами. Позначаються Oxz, Oyz, Oxy. Координатні площини поділяють простір на вісім октантів. Прямокутна ДСК позначається як Oxyz.

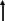
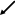
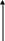
Означення: Прямокутна ДСК називається правою, якщо з кінця вектора найкоротший поворот від вектора до вектора видно проти годинникової стрілки. Якщо ж з кінця вектора найкоротший поворот від вектора до вектора видно по годинниковій стрілці, то СК називається лівою.

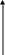
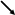
права СК ліва СК

Надалі будемо користуватися правою СК.

Зауваження: У правій СК базисні вектори розташовані так, як розташовані відповідно великий ( ), вказівний ( ) і середній ( ) пальці правої руки.

Нехай задана ПДСК Оxyz. і довільна точка М.

М

0

Означення: Радіус- вектором точки М називається вектор, , що йде від початку координат О до т.М. Розкладемо вектор за базисом

Означення: Координатами точки М в ПДСК називаються координати її радіус-вектора . Точка М з координатами X, Y, Z, позначається через М(x; y; z).

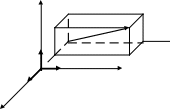Нехай в ПДСК Оxyz задано вектор . Розкладемо вектор за базисом ;

В

А

де числа - координати . Але ; ; .

Означення: Координатами вектора в ПДСК називаються числові проекції вектора на осі координат. Вектор з координатами , , позначається =( , , ).

Зауваження: Замість проекції на осі координат можна брати проекції на осі, що проходять через початок (т.А) вектора в тому ж напрямку, що й координатні