§ 7. Отношения между двумя множествами

С целью уточнения вернемся к вопросу об отношении вклю-^ чения одного множества в другое.

Вообще говоря, в математике различают два вида включения: а) в широком смысле (нестрогое включение) и б) в узком смысле (строгое включение). Первое обозначается знаком £. Запись «Л £В» означает, что все элементы Л принадлежат В. При этом возможны два случая:

ai) все элементы В принадлежат Л, т. е. Л=В и В^А. В этом случае множества А и В состоят из одних и тех же эле­ментов и называются равными, что обозначается так: «Л=В». Например, если А — множество всех больших блоков, а В — множе­ство всех блоков, которые не являются малыми, то А = В. Как видно, равные множества по существу совпадают (при задании их перечислением элементов они могут отличаться лишь поряд­ком перечисления, который несуществен);

аг) не все элементы В принадлежат А, т. е. ЛеВ, но В^А. В таком случае говорят также, что А строго включается в В, или А является собственной (Или правильной) частью В. Это отношение в математической литературе обычно обозначает­ся символом «с» (АаВ).

В предматематической подготовке дошкольников встречается лишь строгое включение, собственная часть множества. Представ­ление о том, что все множество есть несобственная часть самого себя, противоречило бы житейскому опыту. Конечно, никакие спе­циальные обозначения здесь не применяются.

В играх с обручами моделируются и другие отношения, в ко­торых могут находиться два множества. Так например, множества красных (Л) и некрасных (Л) блоков не имеют ни одного общего элемента, т. е. их пересечение пусто (Л ПЛ= 0). Такие два мно-' жества, как мы уже знаем, называются непересекающими­ся (в литературе встречается и термин «дизъюнктные» множества). Множества красных (Л) и квадратных (В) блоков имеют общие элементы (красные квадраты), т. е. их пересечение непусто (ЛПВ^=0), Причем ни одно из этих множеств не включается в другое, т. е. не является подмножеством другого. Такие два множества называются пересекающимися.

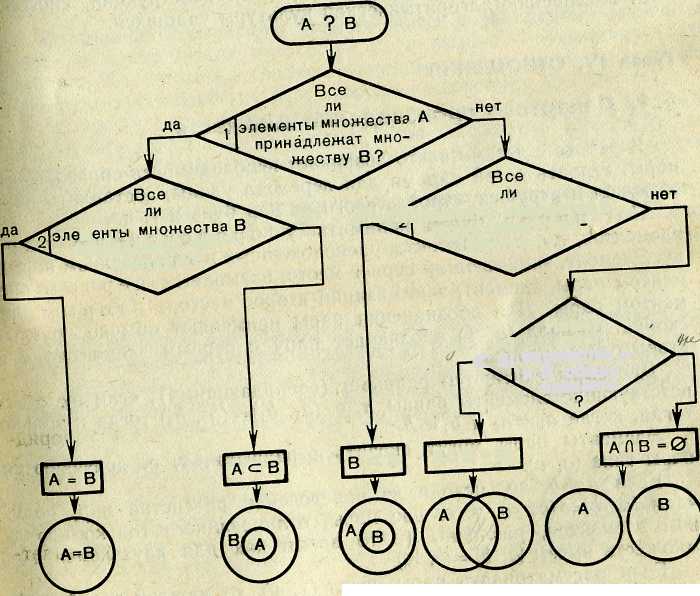
Таким образом, два произвольных множества Л и В могут находиться в одном из пяти отношений, которое можно выявить с помощью последовательности вопросов, представленных на ри­сунке 4. Каждый из этих вопросов требует ответа «да» или «нет» Подобные вопросы, касающиеся конкретных множеств предметов (без названия отношений между множествами), ставятся и перед дошкольниками с целью выявления отношений между множествами окружающих нас предметов. Например, вопрос «Все ли березы — деревья?» получает ответ «да», а вопрос «Все ли деревья — бере­зы?» — ответ «нет» (нужно добиваться обоснования этого ответа: «Имеются и другие деревья, не являющиеся березами, например дубы, тополя, липы, сосны...»). Этими вопросами и выявляется отно­шение включения между множествами берез и деревьев (разумеется, термином «включение» при этом не пользуются). Другой пример: «Все ли автомашины красные?» (Нет.) «Все ли красные пред­меты — автомашины?» (Нет, есть красные флаги, цветы и другие предметы красного цвета.) «Но имеются ли красные автомашины?» (Да.) Этими вопросами выявляется отношение пересечения между множествами красных предметов и автомашин.

Выявление правильных отношений между множествами окружаю­щих нас предметов — составная часть формирования и развития представлений дошкольников об окружающем мире. Выработка у дошкольников простейших представлений классификации окружаю­щих предметов является основой для формирования в дальней­шем математического мышления, связанного с моделированием и исследованием различных математических конструкций, способст­вует повышению алгоритмической культуры учащихся.

Гиава IV. ОТНОШЕНИЯ

. Декартово произведение множеств

В работе с детьми часто возникает необходимость образовывать пары: строить детей парами для перехода улицы, составлять пары из кукол и игрушек, строить слоги из пар букв и т. п.

Под парой будем понимать упорядоченную пару элементов, т. е. два элемента, расположенных в определенном поряд­ке. Элемент, занимающий первое место, называется первым эле­ментом пары, элемент, занимающий второе место,— вторым эле­ментом пары. Для обозначения пары применяют обычно круглые скобки. Символ (а, Ь) обозначает пару с первым элементом а и вторым элементом Ь.

Две пары считаются равными (совпадающими), если их соот­ветствующие элементы равны, т. е. (а\, Ь\)=-{ач, b-i) тогда и только тогда, когда а\=а% и b\-=b%.

Элементы пары могут оказаться равными, т. е. допускаются пары типа (а, а).

Если афЬ, то, исходя из определения равенства пар, полу­чаем (а, Ь)Ф{Ь, а), т. е. две пары, отличающиеся только поряд­ком элементов, различны (в то время как для двухэлементных множеств имеем {a, b)—{b, а}).

Если рассматривать пары чисел (х, у), то каждой такой паре соответствует точно одна (одна и только одна) точка плоскости при заданной системе координат — точка с координа­тами х и у. Если при этом хфу, то {х, у) и {у, х) — различные точки (рис. 5).

Рассмотрим таблицы I и II «открытых» и «закрытых» сло­гов. По существу мы имеем здесь два множества букв: мно­жество согласных С={м, н, п, р} и множество гласных Г={а, е, о, у}.

	а	е	О	У
м	ма	ме	МО	му
II	на	не	Но	ну
п	па	пе	По	пу
р	ра	ре	Ро	РУ

Таблица I Таблица II

	м	н	п	р
а	ам	ан	ап	ар
е	ем	ен	еп	ер
о	ом	он	ен	ор
У	ум	ун	уп	УР

I

В таблице I выписаны всевозможные пары, первые элементы которых принадлежат множеству С, а вторые — множеству Г. В таблице II выписаны всевозможные пары, первые элементы которых принадлежат множеству Г, а вторые — множеству С.

В первом случае множество пар называется декартовым произведением множества С на множество Г (СХГ), во втором — декартовым произведением множества Г на множество

С(ГХС).

Дадим теперь общее определение декартового произведения двух

множеств: декартовым¹ (По имени французского философа и математика Рене Декарта (1596-1650).произведением АхВ множества А на мно­жество В называется множество всевозможных пар, первые эле­менты которых принадлежат А, а вторые — В, т. е. АхВ={(х у)\х£А и у£В).

Ах{( у)

Множество АхВ распознается по тому, что его элементами являются пары элементов двух других множеств (Л и В).Если В=А, то АХВ = АхА={{х, у)\х£А и у£А\ т. е. АХА — множество всевозможных пар элементов из множества Л. Это мно­жество пар обозначается также символом Л².