§ 2. «Вычислительные машины»

Речь пойдет, разумеется, о детских играх, поэтому слова «вы­числительные машины» взяты в кавычки. Прежде всего рассмотрим серию игр, в которых под термином «вычислительные машины» понимают блок-схемы несложных вычислительных процессов.

На рисунке изображена простейшая «вычислительная ма­шина», умеющая выполнять только одно действие — «прибавлениеединицы».

Рис. 30.

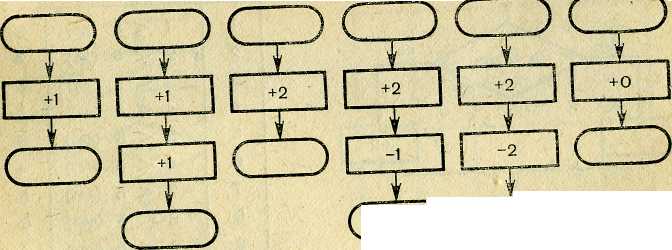
Если один из участников игры задает на входе машины какое-нибудь число, например 3, размещая в верхней овальной фигуре карточку с соответствующей цифрой, то другой участник, выполняю­щий роль «вычислительной машины», должен положить на выход карточку с результатом, т. е. с числом 4. Если он ошибочно кладет другую карточку, то ее отбирают. Проигрывает тот, у кого не хва­тает карточек с цифрами для продолжения игры.

«Вычислительная машина» постепенно усложняется. На рисунке 30,2 изображена «машина», последовательно выполняющая дейст­вие «прибавление единицы» дважды.

Возникает вопрос: нельзя ли усовершенствовать «гвычислительную машину», выполняющую два одинаковых действия «прибавление единицы», заменив ее другой, выполняющей лишь одно действие? Такая «машина» изображена на рисунке 30,3. В процессе игры подтверждается, что если на входы этих двух «вычислительных машин» попадут карточки с одинаковыми числами, то на их выходах окажутся также карточки с одинаковыми числами, т, е. эти «машины» действуют одинаково, тем самым доказывается тождество

(а+ 1)+ 1 =а + 2 для любого а.

Аналогично в ходе игры с использованием «машины», изображен­ной на рисунке 30,4, обнаруживается, что последовательное выпол­нение двух действий « + 2»— прибавление числа 2 и «—1» — вычитание единицы, равносильно выполнению одного действия « + 1» — прибавление единицы. Следовательно, «машины», изоб­раженные на рисунках 30,/ и 30,4, действуют одинаково ({а + 2) — 1 = = а+1 для любого а). Целесообразно также проведение игры с использованием «машины», изображенной на рисунке 30,5. Можно вместо действий « + 2» и «— 2» взять « + 3» и «— 3» или «-J-1» и «— 1». Проверив для нескольких различных чисел работу этой «машины», дети обнаруживают, что она не меняет исходного числа, т. е. они уже открывают для себя то, что в дальнейшем запи­шут в виде предложения «(а + 2) — 2 = а для любого а» или вообще «(а + 6)— Ь = а для любых а и 6».

«Машину», изображенную на рисунке, можно заменить ей

а	а <	: 5		?
1	1 <	С 5	(да)	3
2	2 <	С 5	(да)	4
3	3 <	Z 5	(да)	5
4	4 <	С 5	(Да)	6
5	5 <	С 5	(нет)	3
6	6 <	С 5	(нет)	4
7	7 <	С 5	(нет)	5
8	8 <	С 5	(нет)	6
9	9 <	=С 5	(нет)	7

«равносильной», изображенной на рисунке 30,6, моделирующей тождество а + 0 = а для лю­бого а.

Изображенные на рисунке 30 «машины» представляют простейшие линейные алгорит­мы. Проводимые эксперименты подтверждают, что дети 5—6 лет легко усваивают и работу «машин», представляющих про­стейшие разветвленные и цик­лические алгоритмы.

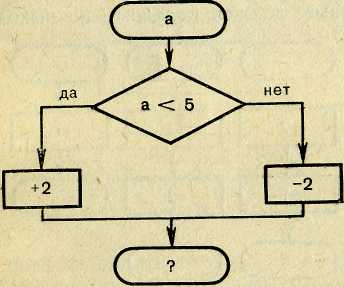
Изображенная на рисунке 31,1 «машина» работает сле­дующим образом: если на вход «машины» подано некоторое число а, «машина» прежде всего проверяет, выполняется ли условие «а<5». Если оно выполняется, то «машина» прибавляет к данному числу 2, если не выполняется, то вычитает 2. Знак вопроса на выходе «машины» нужно заменить полученным результатом. На рисунке 31,2 дана таблица, показывающая работу этой «машины» для значений а: 1, 2, 3, 4, 5, 6, 7, 8, 9.

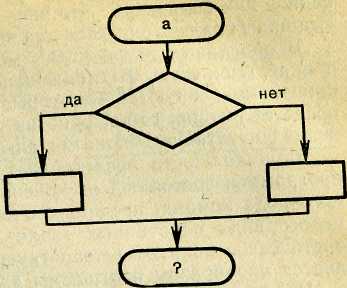
Можно использовать «машины» этой же структуры, но с другими условиями и действиями. Для этой цели изготавливается на боль­шом листе бумаги «машина» с пустыми блоками (рис. 32), в которые вносятся различные условия (в ромбе) и различные действия

(в прямоугольниках).

На рисунке 33,/ изображена «машина», представляющая цикли­ческий алгоритм: если на вход подано некоторое число а, то «машина» прибавляет к нему 2, если полученное число меньше 9, она опять прибавляет 2 и т. д., пока не получится число, не меньшее 9, т. е.

а +2			< 9	?
1	3	3 <	: э	(Да)
	5	5 <	; э	(да)
	7	7 <	; э	(да)
9		9 <	' 9	(нет)	9
2 4		4 <	С 9	(Да)
	6	6 «	С 9	(Да)
	8	8 -	£ 9	(Да)
	10	10 -	< 9	(нет)	10

Рис. 32.

Рис.31

.

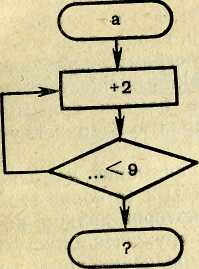
равное или большее 9. Это число и будет результатом. Работа этой «машины» иллюстрируется для чисел 1 и 2 в таблице на рисунке 33,2. В описанных выше играх моделируются различные алгоритмы в виде блок-схем. В следующей серии игр «Вычислительные ма­шины» моделируются некоторые алгоритмы в виде машин Поста, представляющих собой одно из разработанных в математике уточнений интуитивного понятия алгоритма.

Машина Поста представляет собой точное предписание в виде программы, состоящей из конечной последовательности определен­ного рода команд, предназначенной для решения любой задачи из целого вида однотипных задач. Хотя машина Поста — чисто те­оретическое понятие («теоретическая машина»), ее программа яв­ляется прообразом программы для реальной ЭВМ.

Профессор МГУ В. А. Успенский в своей популярной брошюре «Машина Поста» (М., 1979.— С. 4) говорит о том, что школьники первых классов и даже старшие дошкольники без труда могут осуществлять «вычисления» на машине Поста по заданной програм­ме, например, при помощи разграфленной на секции бумажной ленты и канцелярских скрепок или пуговиц в качестве меток, а также составлять простейшие программы (не содержащие команд передачи управления). Это высказывание В. А. Успенского под­тверждается и проводимыми экспериментами. Опишем две простей­шие машины Поста, осуществляющие «прибавление единицы».

Память машины представляет собой ленту, разделенную на клетки. Каждая клетка памяти может хранить определенный знак (в качестве такого знака мы использовали красный кружочек, вырезанный из картона), в таком случае она считается заполнен­ной, а в противном случае — пустой. Машина в любой момент «смотрит» лишь на одну клетку памяти и может выполнить следую­щие действия: а) «передвинуть свое внимание» (осуществить сдвиг) на одну клетку вправо или влево; б) положить кружочек в обозре­ваемую клетку, если она пуста; в) вынуть кружочек из обозре­ваемой (в данный момент) клетки, если она заполнена. Если машине поступает команда положить кружочек в уже заполнен­ную клетку или вынуть кружочек из пустой клетки, то она «ломается».

На рисунке 34,1 изображена простейшая программа прибавле­ния единицы, а на рисунке 34,2 показано,. как выполняется эта программа, если в начале работы машины в памяти хранятся три кружочка, а машина «смотрит» на самую правую заполненную клетку, что обозначено стрелкой.

По команде 1 машина «передвигает» свое внимание на одну клетку вправо и переходит к выполнению команды 2 (в конце этой команды указан номер команды, к выполнению которой должна пе­реходить машина). По команде 2 машина кладет кружочек в пустую клетку, на которую она смотрит, и переходит к выполнению команды 3 («стоп»), по которой останавливается.

Если эту программу применить к начальному состоянию, изобра­женному на рисунке 34Д то машина сломается, так как командой 100

0		•	®	*
			1
2					<

Стоп 2

Машина сломалась 3

Рис. 34,

2 ей предписано положить кружочек в заполненную клетку. Значит, для случая, когда машина «смотрит» вначале не на самую правую заполненную клетку, эта машина не годится, нужна более совершен­ная программа прибавления единицы. Такая программа изображена на рисунке 35,1.

На рисунке 35 имитируется работа этой машины.

По команде 1 машина совершает сдвиг вправо на одну клетку и переходит к выполнению команды 2. Команда 2 выполняется в зависимости от того, «смотрит» машина в данный момент на пустую или на заполненную клетку. В нашем случае машина «смот­рит» на заполненную клетку. Поэтому надо смотреть на нижнюю стрелку команды 2, на которой нарисована заполненная клетка. Она указывает на то, что нужно возвратиться (еще раз выпол­нить) к команде 1. По этой команде машина еще раз «сдвигается» вправо на одну клетку и переходит к выполнению команды 2. Теперь, так как машина «смотрит» . на пустую клетку, верхняя стрелка команды 2, на которой нарисована пустая клетка, указывает,

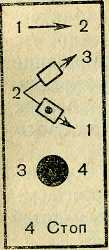
°П		•1	•1	•1	И	!	1	!	<
i|		•	•	•1
	1 1
2		•	•	®
					I _
3				© в

_Т

Стоп

Рис. 35.

	( Начало J
да
		К

что надо перейти к выполнению команды 3. По команде 3 маши­на кладет в пустую клетку, на которую она «смотрит», кружо­чек и переходит к выполнению команды 4. По команде 4 ма­шина останавливается.

Конец

Дети с увлечением имити­руют работу машины при раз­личных начальных состояниях. После имитации работы вычи­слительной машины рекомен­дуется показать им с помощью карточек с цифрами и знаками + и =, какое действие вы­полнила машина (рис. 35,<3), что с успехом выполняют са­ми дети. Повторяя эту игру для различных исходных чисел (кружочков в памяти машины), дети могут самостоятельно по­лучить таблицу прибавления единицы: 1 + 1=2; 2 + 1=3; 3+1=4; ...; 9+1 = 10.

Рис. 36.

Нетрудно заметить, что последняя программа представляет опре­деленным образом записанный циклический алгоритм, который можно задать и с помощью блок-схемы (рис. 36).

Можно разработать игры, использующие и простейшие програм­мы вычитания 1, прибавления 2 и некоторые другие.

Отметим в заключение, что приведенные в этом параграфе игры типа «Вычислительная машина», а также им подобные открывают хорошие возможности для раннего внедрения в обучение простей­ших идей информатики, способствующие повышению развивающего эффекта обучения, формированию некоторых умений, характери­зующих операционный стиль мышления и, что особенно важно, уме­ния расчленять сложные действия на элементарные составляющие и представлять их в виде организованной совокупности последних, умения планировать свои действия, умения строго придерживаться определенных правил, умения выражать свои действия адекватными языковыми средствами и др.

Вряд ли нуждается в доказательстве важность этих умений в человеческой деятельности, необходимость и возможность как можно более раннего начала работы по их формированию у детей.