VII. Величины и их измерение

Глава

внутренней точки можно найти окрестность, внутри которой все точки принадлежат территории СССР. Для любой точки на гра­нице СССР такой окрестности нет, т. е. в любой окрестности такой точки найдутся как точки, принадлежащие СССР, так и точки, принадлежащие сосед­нему государству.

Среди форм используемых нами блоков (или фигур), кро­ме треугольника, квадрата, пря­моугольника, имеется и круг. Кроме того, многие предметы, с которыми встречаются дети (тарелки, блюдца, колеса вело­сипеда и др.), имеют круглую форму. Считаем нецелесообраз­ным для дошкольников вводить термин «окружность».

В элементарной геометрии круг определяется как множе­ство (или геометрическое место) всех точек плоскости, удаленных от некоторой точки, называемой центром, на расстояние, не превышающее R (/? —радиус круга); окружность определяется аналогично как множество всех точек плоскости, удаленных от точки, называемой центром, на одно и то же расстояние R.

Рис. 19.

Заметим, что если в этих формулировках слово «плоскость» за­менить словом «пространство», то получим определения шара и сфе­ры, соответственно пространственных аналогов круга и окружности. Круг, окружность, шар и сферу можно определить и генети­чески, т. е. описанием процесса образования этих фигур. Этот процесс легко смоделировать: если отрезок зафиксировать в од­ном конце и вращать его около этого конца, то он опишет круг, а второй его конец — окружность. Если полукруг вращать около диаметра, то он опишет шар, а ограничивающая его полуокруж­ность — сферу.

Дошкольники знакомятся также с одним из простейших много­гранников, каким является куб.

Куб — пространственный аналог квадрата. Он ограничен шестью квадратами. Его можно сконструировать (склеить) из плоской фи­гуры выкройки, изображенной на рисунке 19.

Ознакомление детей с описанными выше простейшими геомет­рическими фигурами является пропедевтической основой для даль­нейшего формирования и развития у них геометрических, в том числе пространственных, представлений.

Глава VII.Величины и их измерение

§ 1. Что такое величина!

Величина — одно из основных математических понятий, воз­никшее в древности и подвергшееся в процессе длительного разви­тия ряду обобщений.

Общее понятие величины является непосредственным обобще­нием более конкретных понятий: длины, площади, объема, массы, скорости и т. п. Каждый конкретный род величин связан с опре­деленным способом сравнения соответствующих свойств объектов. Например, в геометрии отрезки сравниваются при помощи наложе­ния и это сравнение приводит к понятию длины: два отрезка име­ют одну и ту же длину; если при наложении они совпадают; если же один отрезок накладывается на часть другого, не покрывая целиком, то длина первого меньше длины второго. Общеизвестны более сложные приемы, необходимые для сравнения площадей плос­ких фигур, объемов пространственных тел.

Для сравнения двух предметов по массе их взвешивают. Если чаши весов уравновешиваются, то предметы имеют одинаковую мас­су, если же чаши не уравновешены, то предмет, находящийся на той чаше, которая перетягивает, имеет большую массу, второй предмет —

меньшую.

Понятия длины, площади, объема, массы могут быть обобще­ны на любой род величин: в системе всех однородных величин, т. е. всех длин, всех площадей, всех объемов, всех масс и т. д., устанавливается отношение порядка. Две величины а и Ь одного и того же рода или совпадают {а = Ь\ или первая меньше второй (в<6), или вторая меньше первой (6<а).

Однородные величины можно также складывать. Например, если точка В лежит между точками Л и С, то длина отрезка АС равна сумме длин отрезков АВ и ВС (рис. 20, /).

Если плоская фигура состоит из двух частей, не имеющих других общих точек, кроме граничных, то площадь S всей фи­гуры равна сумме площадей S1-T-S2 этих частей (рис. 20,2).

а + в

Е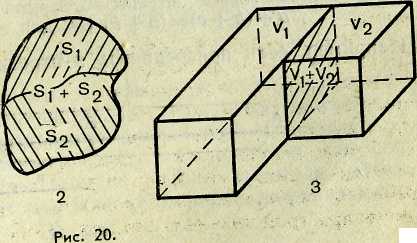 сли пространственная фигура состоит из двух частей, все

общие точки которых образуют их общую границу, то объем V всей пространственной фигуры равен сумме Vi + V2 объемов H^D Vi и Vi этих частей (рис. 20,3). "* Если предмет состоит из двух

частей, то его масса т равна -¹ сумме т.\А_гтг масс т\ и т₂ этих частей.

Так раскрывается смысл опе­рации сложения для каждого рода величин (длин, площадей, объемов, масс и т. д.).

Исходя из смысла отношения «меньше» (<■) и операции сложе­ния однородных величин (+) можно убедиться в том, что любая система однородных величин (В, <, +) обладает перечисленными ниже свойствами.

1. Отношение «о является, как и между числами, ан­ тирефлексивным, т. е. ~\ (а<Са) для любого а£В; асимметрич­ ным (для любых а, Ь£В, если а<Ь, то П6<а) и транзитивно (для любых а, Ь, с£В, если а<6 и 6<с, то а<с), т. е. является отношением строгого порядка. Причем для любых а, Ь, с£В, если афЬ, то a<Cb или b<а, т. е. система однородных величин В упоря­ дочена этим отношением.

2. Если а<.Ь, то существует величина с 6 Втакая, что а + с = Ь. Величина с называется разностью между величинами b и а и обозначается «6 — а», т. е. а-\-с = Ь равносильно с = Ь — а. Например, если взять два отрезка, АВ длины а и CD длины Ь, причем a<ib, и отложить на отрезке CD отрезок СВ\, равный АВ, то образо­ вавшийся отрезок B\D будет иметь длину с = Ь — а (рис. 21).

3. Сложение величин, как и сложение чисел, обладает свойством переместительности (коммутативности):

a-\-b = b-\-a для любых а, Ь£В.

Например, безразлично присоединить к отрезку АВ длины а отрезок ВС длины b или наоборот, получим один и тот же отрезок.

4) Сложение величин обладает свойством сочетатель­ ности (ассоциативности):

a-\-(b + c)=(a-\-b)-\-c для любых а, Ь, с£В. Например, если присоединить к отрезку АВ длины а отрезок BD

а + в

D

в + с

Рис. 22.

длины 6 +с так, чтобы точка В лежала между точками А и D (рис. 22), то получим отрезок AD длины а + (Ь + с); если к отрезку АС длины а-\-Ь присоединить отрезок CD длины с, то получим тот же отрезок AD, его длина выражается через {а-\-Ь)-{-с; но так как мы получили один и тот же отрезок AD, то a-{-(b-{-c) = (a-+-b)-\-c. Поэтому можно писать без скобок a + fe-f-c.

5) Для любых а, 66В, а-\-Ь>а (свойство монотонности сложения). Например, если точка В лежит между точками А и С (рис. 20, /), то длина отрезка АС(а + Ь) больше длины отрезка АВ (а), или вообще «величина части меньше величины целого».

6) Всякую величину а£В можно делить на 2, 3, 4 и вооб­ ще на любое число п одинаковых частей, иными словами, для любой величины а^В существует величина Ь£В такая, что пЬ — а.

I Величина Ъ называется м-й долей величины а.

7) Допустим, что имеется некоторый отрезок АВ длины а и другой отрезок CD длины Ъ. Какими бы ни были отрезки АВ и CD, можно наложить отрезок CD на отрезок АВ такое большое число п раз, что получим отрезок длины nb, превышающей а. Таким образом, какие бы ни были величины а, Ь£Ц, всегда суще­ ствует натуральное число п такое, что a<.nb.

Перечисленные свойства 1)— 7) системы величин (В, <, +) интуитивно ясны и допускают наглядное истолкование на конкрет­ном примере системы длин отрезков. Отметим, что эти свойства еще не составляют полной характеристики системы однородных величин. Для получения такой характеристики они должны быть до­полнены еще одним свойством с более сложным содержанием и не допускающим столь наглядное истолкование, так как оно связано

: с категорией бесконечности.

8) Предположим, что даны две последовательности однородных величин: (1) ои, a-i, ... , а_п, ... и (2) Ь\, Ьч, ... , Ь_п, ... , при­чем (1)—возрастающая, т. е. а.1<.а2<....<.ап<..~, а (2) — убывающая, т. е. b\ >bi >...!> Ь„> ... . Кроме того, любая величи­на первой последовательности меньше любой величины второй и с увеличением номера п члены этих последовательностей прибли­жаются друг к другу как угодно близко, т. е. какую бы ни взяли величину с при достаточно большом номере п, разность Ь_п — а_п ста­новится меньше с (Ь_п — а_п<.с). При этих условиях существует единственная величина х, которая больше всех й_п и меньше всех Ь_п, т. е. неравенство

выполняется для любого номера п членов последовательностей. Как же следует ответить на вопрос «Что такое величина?». Прямого ответа в виде определения («величиной называется...») мы не приводим. На поставленный вопрос мы ответили косвенно: привели конкретные примеры величин (длина, площадь, объем, масса) и на этих примерах выявили свойства, характеризующие любую величи