4. Основні середні статистичні величини

Середня арифметична (М) - найбільш поширений статистичний показник середньої величини ознаки у відібраній групі особин. Середня арифметична є основною характеристикою модифікаційної мінливості. Існує загальноприйнята формула для розрахунку середньої арифметичної:

де: - знак суми;

n - кількість особин в групі;

V- значення ознаки (дата) у кожної особини в групі.

Мода (М₀) - варіанта або значення, які найчастіше зустрічаються у дослідній

групі (виборці). Моду найчастіше використовують для характеристики якісних ознак.Значення моди при великій кількості спостережень та розбиванні на класи розраховується за формулою:

де: V_Мо- початок модального класу;

К - величина класу;

р₁- частота класу, яка передус модальному;

р₂- частота модального класу;

р₃- частота класу, яка слідує за модальним.

Медіана (М_е) - варіанта, яка розміщена в центрі варіаційного ряду і значення якої поділяє всю сукупність спостережень на дві рівчі частини. Тобто ми маємо рівну кількість значень ознаки, які перевершують медіану, і стільки ж значень, які менше медіани. Медіана розраховується за формулою:

де: V_Mе- початок класу, В якому знаходиться значення медіани;

K - величина класу;

i₁ - число варіантів або сума накопичених частот, що відповідають половині всіх спостережень

Р_Ме - частота медіанного класу;

і₂ - число варіантів або сума накопичених частот, що передують класу, який включає медіану.

У тваринництві моду та медіану використовують для додаткової характеристики дослідних груп, порід, типів, ліній та потомства оцінюваних батьків.

5. Показники різноманітності ознак

Для повної характеристики сукупності об'єктів, які включені у вибірку, недостатньо лише середніх величин. Тому другим істотним показником будь-якої сукупності є величина мінливості (варіювання) значень даної ознаки у особин. Вимірювання ступіні різноманітності статистичними методами можливе як для кількісних, так і для якісних ознак.

Основні показники, які характеризують мінливість ознак:

Ліміт - це різниця між максимальним та мінімальним значенням ознаки у дослідній групі. Чим більше різниця між значеннями, тим різноманітніше ознака. Ліміт розраховується за формулою:

дисперсія (варіанса, середній квадрат) (², s²) - середній квадрат відхилень. який вимірює мінливість ознаки і виражає її через середній квадрат відхилення кожного члена сукупності від середньої арифметичної даної ознаки. Формула для розрахунку незміщеної (неснещенной- рос.) дисперсії:

де:  -знак суми;

n - кількість особин у групі (об'єм вибірки),

n -1 - число ступенів свободи;

V - значення ознаки (дата) у кожної особини у групі;

M - середня арифметична ознаки певної групи.

Дисперсія переважно використовується при проведенні дисперсійного аналізу.

Середи» квадратичне відхилення (стандартне відхилення, сигма) () - найбільш поширене статистична величина для виміру мінливості, яка показує наскільки в середньому кожна варіанта відхиляється від середньої арифметичної даної вибірки. Чим більше значення середнього квадратичного відхилення, тим більше мінливість даної ознаки в сукупності. Сігма використовується для порівняння однакових ознак, характеризує всю групу в цілому і виражається в тих же одиницях, що й ознака. Середнє квадратичне відхилення - це квадратний корінь з незміщеної дисперсії.

Зараз існує багато формул для розрахунку середнього квадратичного відхилення, всі вони дають практично однакові результати, а їх застосування залежить від можливостей технічних засобів. Основна формула для розрахунку сигми:

;

Отже:

де: С - дисперсія або сума квадратів центральних відхилень;

V - значення ознаки (дата) у кожної особини у групі;

М - середня арифметична ознаки певної групи.

- сума квадратів значень ознак;

квадрат суми;

n - кількість особин у групі (об'єм вибірки);

n -1 - число ступенів свободи.

Середнє квадратичне відхилення використовують як самостійний показник, так і в розрахунках інших біометричний показників: коефіцієнтів варіації, кореляції, регресії, помилок репрезентативності середніх величин, різних показників розподілення, елементів дисперсійного аналізу.

Коефіцієнт варіації (Cv) - показує ступінь мінливості різнойменних ознак в певній дослідній групі або однойменних ознак в різних групах і виражається у відсотках. Коефіцієнт варіації використовують у біологічних дослідженнях, якщо виникає потреба порівняти показники, які мають однакові або різні одиниці виміру. Формула розрахунку:

,

де:  - середнє квадратичне відхилення;

М - середнє арифметичне.

Чим більше значення коефіцієнта варіації, тим вища мінливість ознаки у об'єктів вибірки на практиці прийнято розрізняти слабку мінливість (Cv5%), середню (Cv=5-15%) та сильну (Cv15%).

Алгоритм 1. Розрахунок n, M, , m, Cv за допомогою вмонтованих статистичних функцій Excel та самостійно введених формул

Крок	Назва операції
Розрахунок n
1	Ставимо курсор в клітинку, де планується отримати значення кількості дат, варіантів або кількості особин: Е23
2	Ставимо знак „=”, потім на панелі стандартних інструментів натискаємо піктограму fx Вставка функции
3	Вибиваємо категорію: Статистические
4	Вибирасмо функцію: СЧЕТ. натискаємо ОК
5	Розкривається меню" Счёт», в яке за допомогою курсору або ручним способом вводимо інтервал даних (E2:Е21) в: Значение 1 , натискаємо ОК
6	У клітинці Е23 з'являсться розрахований показник n
Розрахунок M
7	Ставимо курсор в клітинку, де планується отримати значення середньої' арифметичної: Е24
8	Ставимо знак "=", потім на панелі стандартних інструментів натискаємо Піктограму: Мастер фуннций
9	Вибираємо категорію: Cmaтucrnические
10	Вибираємо функцію: СРЗНАЧ, натискаємо ОК
11	Розкривається меню 'СРЗНАЧ", в яке за допомогою курсору або ручним способом вводимо ін-тервал цих же даних (E2:E21) в: Число 1, натискаємо ОК.
12	У клітинці Е24 з'являється розрахований показник М
	Розрахунок 
13	Ставимо курсор в клітинку, де планується отримати значення середнього квадратичного відхилення: Е25
14	Ставимо знак '=', потім на панелі стандартних інструментів натискаємо піктограму: Macmep функцій
15	Вибираемо категорію: Статистические
16	Вибираємо функцію: СТАНДОТКПОН, натискаємо ОК
17	Розкривається меню "СТАНДОТКЛОН", в яке за допомогою курсору або ручним способом вводимо інтервал цих же даних (Е2:Е21) в: Число 1, натискаємо ОК
18	У клітинці Е25 з'являється розрахований показник 
	Розрахунок m
19	Ставимо курсор в клітинку, де планується отримати значення помилки середньої арифметичної: Е26
20	Ставимо знак "=", потім вводимо формулу для розрахунку в цю клітинку: =Е25/(КОРЕНЬ(Е23)). При цьому вказуємо, що в клітинці Е25 -значення сигми, знак ділення - ставимо "/", корінь квадратний - вказуємо КОРЕНЬ, та n беремо з клітинки (Е23).
21	У клітинці Е26 з'являється розрахований показник m
	Розрахунок Сv
22	Ставимо курсор в клітинку, де планується отримати значення коефіцієнта варіації: Е27
23	Ставимо знак „=", потім вводимо формулу для розрахунку в цю клітинку: =Е25/E24*100. При цьому вказуємо, що в клітинці E25 - значення сигми, знак ділення - ставимо „/”.що в клітинці Е24 - значення середнього арифметичного, ставимо знак помножітги "*", пишемо 100
24	У клітинці Е27 з'являється розрахований показник Cv

Знак "=" в відведеній клітинці можна не вводити, а зразу ж натискати піктограму: Мастер функций. Якщо деякі функції використовуються дуже часто, то момна користуватись категорією: 10 недавно использоеавшихся.

Таким чином ми розрахували статистичні показники для ознаки "Надій натері”:

n	20
м	4355,1
Сігма	1346,76
m	301,1447
Cv,%	30,92375

Щоб розрахувати ці ж показники для інших ознак необхідно скопіювати введені формули для інших ознак (надій, вміст жиру в молоці, жива маса, висота в холці, обхват грудей). Для цього слід виконати такі операції:

1) відмітити блок клітин з формулами: Е23:Е27;

2) підвести курсор в праву нижню частину відміченого блоку, при цьому покажчик миші повинен змінити свою форму на тоненький хрестик;

3) при натиснутій лівій клавіші миші протягнути відмічений блок по колонках: F, G. H, I тa J.

4) у встановленому інтервалі автоматично з'являться статистичні показники для всіх інших ознак (мал. 2):

Малюнок 2. Розраховані основні статистичні показники за допомогою функцій Excel та самостійно введених формул

Алгоритм 2. Розрахунок основних статистичних показників за допомогою Пакету аналізу

Крок	Назва операції
1		На панелі меню лівою клавішею миші розкриваємо меню: Сервис - Анализ данных
2		Далі вибираємо: Инструменты анализа - описательная статистика, натискаємо ОК
3		Розкривається меню: Описательная статистика, де за допомогою лівої клавіші миші вводимо Входной интервал: $E$2:$J$21. відмічаємо: Итоговая статистика, Уровень надежности, К-ый наименьший. К-ый наибольший, натискаємо ОК
4		На новому аркуші з'являться розраховані основні статистичні показники (мал. 3)

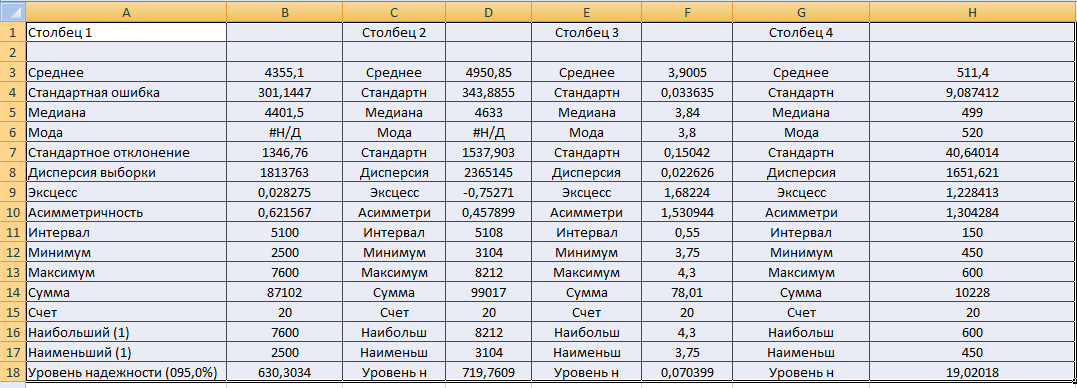
Малюнок 3. Розраховані основні статистичні показники за допомогою Пакету аналізу

Існує ще один спосіб розрахунку статистичних показників, але це краще використовувати у випадку коли застосовувалось сортування даних. Для цього потрібно послідовно виконати такі операції:

1) на панелі меню лівою клавішею миші розкрити меню: Данные - Итоги,

2) за допомогою лівої клавіші миші вказуємо які потрібно виконати операції та для яких ознак, натискаємо ОК.