Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сумский национальный аграрный университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Met_ZOO_excel2013.doc

Скачиваний:

Добавлен:

01.07.2025

Размер:

1.65 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1010

12. Додатки

Додаток 1. Стандартні значення критерія вірогідності по Ст'юденту (t_st) при трьох рівнях ймовірності (Р) і різних числах ступенів свободи ( )*.

Число ступенів свободи ()	Рівень ймовірності (Р)			Тід.ли ступеніе свободи (v)	Рівень ймовірності (Р)
	0,95	0,99	0,999		0,95	0,99	0,999
	значення t				значення t
1	12,71	63,56	637,0	19	2,09	2,86	3,88
2	4,30	9,93	31,60	20	2,09	2,85	3,85
3	3,18	5,84	12,94	21	2,08	2,83	3,82
4	2,78	4,60	8,61	22	2,07	2,82	3,79
5	2,57	4,03	6,86	23	2,07	2,81	3, 77
6	2,45	3,71	5,96	24	2,06	2,80	3,75
7	2,37	3,50	5,41	25	2,06	2,79	3,73
8	2,31	3,36	5,04	26	2,06	2,78	3,71
9	2,26	3,25	4,78	27	2,05	2,77	3,69
10	2,23	3,17	4,59	28	2,05	2,76	3,67
11	2,20	3,11	4, 44	29	2,05	2,76	3,66
12	2,18	3,06	4,32	30	2,04	2,75	3,65
13	2 16	3,01	4,22	35-39	2,03	2,72	3,59
14	2,15	2,98	4,14	40-44	2,02	2,70	3,55
15	2,13	2,95	4,07	45-60	2,01	2,66	3,50
16	2,12	2,92	4,02	70-100	1,98	2,63	3,39
17	2,11	2,90	3,97	120 і більше	1,96	2,58	3,29
18	2,10	2,88	3,92

- величини t_st можна використовувати для:

1) визначення вірогідності середньої арифметичної однієї вибірки;

2) визначення вірогідності між середніми арифметичними двох вибірок;

3)визначення вірогідності r та  при n100.

Додаток 2. Значення ймовірності Р (tt₁) за розподіленням Ст’юдента (при визначенні критерія вірогідності різниці на одній групі в динаміці)

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	
0,0	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,000	1,0000
0,1	0,937	0,929	0,927	0,925	0,924	0,924	0,923	0,923	0,922	0,922	0,922	0,922	0,922	0,922	0,922	0,922	0,921	0,921	0,921	0,921	0,920
0,2	874	860	854	851	849	848	847	846	846	845	845	845	844	844	844	844	844	844	844	844	8415
0,3	814	792	784	779	776	774	773	772	771	770	770	769	769	769	768	768	768	768	767	767	7642
0,4	758	728	716	710	706	703	701	700	698	697	697	696	969	695	694	694	694	694	694	693	6892
0,5	705	667	651	643	638	635	632	631	629	628	627	626	625	625	624	623	623	623	623	623	6171
0,6	656	609	591	581	575	570	567	565	563	562	651	560	559	558	557	557	556	556	556	555	5485
0,7	611	556	534	523	515	510	507	504	502	500	498	497	496	495	495	494	493	493	492	492	4839
0,8	570	508	482	469	460	454	450	447	444	442	441	439	438	437	436	435	435	434	434	433	4237
0,9	533	463	434	419	409	403	398	394	392	389	387	384	384	383	382	381	381	380	379	379	3681
1,0	500	423	391	374	363	356	351	347	343	341	339	384	336	334	333	332	331	331	330	329	3173
1,1	470	386	352	333	321	313	308	303	300	297	295	337	291	290	289	288	287	286	285	284	2713
1,2	442	353	316	296	284	275	269	264	261	258	255	293	252	250	249	248	247	246	245	244	2301
1,3	417	323	284	263	250	241	235	230	226	223	220	253	216	215	213	212	211	210	245	244	2301
1,4	395	296	256	234	220	211	204	199	195	192	189	218	185	183	183	182	179	179	178	177	1615
1,5	374	272	231	208	194	184	177	172	168	165	162	187	158	156	154	152	151	151	150	149	1336
1,6	356	251	208	185	170	161	154	148	144	141	138	159	134	132	130	129	127	127	126	125	0109
1,7	339	231	188	164	150	140	133	128	123	120	117	136	113	111	110	108	106	106	105	105	0896
1,8	323	214	170	145	132	122	115	110	105	102	099	115	095	093	092	091	089	089	088	087	0711
1,9	308	196	154	130	116	106	099	094	090	087	084	197	080	078	077	076	074	074	073	072	0579
2,0	295	184	139	116	102	092	086	081	077	073	071	082	067	065	061	063	061	061	060	059	0154
2,1	283	171	127	104	090	080	074	069	065	062	060	069	056	054	053	052	050	050	049	049	0355
2,2	272	159	115	093	079	070	064	059	055	052	050	058	046	045	044	043	041	041	040	040	0277
2,3	261	148	105	083	070	061	055	050	047	044	042	048	039	038	036	035	0,34	0,34	033	032	0218
2,4	251	130	096	074	062	053	047	043	040	037	035	040	032	031	030	029	027	027	027	026	0164
2,5	242	130	088	067	054	047	041	037	034	031	030	034	027	025	024	024	022	022	022	021	0124
2,6	234	122	080	060	048	041	035	032	029	026	025	028	022	021	020	019	018	018	018	017	0093
2,7	226	114	074	054	043	036	031	027	024	022	021	023	018	017	016	016	015	015	014	014	0069
2,8	218	107	068	049	038	031	027	023	021	019	017	019	015	014	013	013	012	012	011	011	0051
2,9	211	101	063	044	034	027	023	020	018	016	014	016	012	012	011	010	010	010	009	009	0037
3,0	205	095	058	040	030	024	020	017	015	013	012	013	010	010	009	008	008	008	007	007	0027
3,1	199	090	053	036	027	021	017	015	013	011	010	011	008	008	008	007	006	006	006	005	0019
3,2	193	085	048	033	024	019	015	013	011	009	008	009	007	006	006	006	005	005	005	004	0014
3,3	187	081	045	030	021	016	013	011	009	008	007	008	006	005	005	004	004	004	004	004	0010
3,4	182	077	042	027	019	014	011	009	008	007	006	006	005	004	004	004	003	003	003	003	0007
3,5	177	073	039	025	017	013	010	008	007	006	005	005	004	004	004	003	002	003	002	002	0004
3,6	172	069	037	023	016	011	009	007	006	005	004	003	003	003	002	002	002	002	002	002	0003
3,7	168	066	034	021	014	010	008	006	005	004	004	003	002	002	002	002	002	002	001	001	0002

Продовження додатка № 2

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	
3,8	164	063	0,32	0,19	013	009	007	005	004	003	003	003	002	002	002	001	001	001	001	001	0001
3,9	160	060	030	018	011	008	006	005	004	003	002	003	002	002	001	001	001	001	001	001	0001
4,0	156	057	029	016	010	007	005	004	003	002	002	002	002	001	001	001	001	001	001	001	0001
4,1	152	055	026	015	009	006	005	003	003	002	002	002	001	001	001	001	001	001	001	001	0000
4,2	149	052	025	014	008	006	004	003	002	002	001	002	001	001	001	001	001	001	000	000
4,3	145	050	023	013	008	005	004	003	002	001	001	001	001	001	001	001	000	000
4,4	142	048	022	012	007	005	003	002	002	001	001	001	001	001	000
4,5	139	046	020	011	006	004	003	002	001	001	001	001	000	000
4,6	136	044	019	010	006	004	002	002	001	001	001	000
4,7	133	042	018	009	005	003	002	002	001	001	001
4,8	131	041	017	009	005	003	002	001	001	001	001
4,9	128	039	016	008	004	003	002	001	001	000	000
5,0	126	038	015	007	004	002	002	001	001	000
5,2	121	035	014	007	003	002	001	001	001
5,4	117	033	012	006	003	002	001	001	000
5,6	112	030	011	005	003	001	001	001
5,8	109	028	010	004	002	001	001	000
6,0	105	025	009	004	002	001	001

Додаток 3. Стандартні значення Фішера 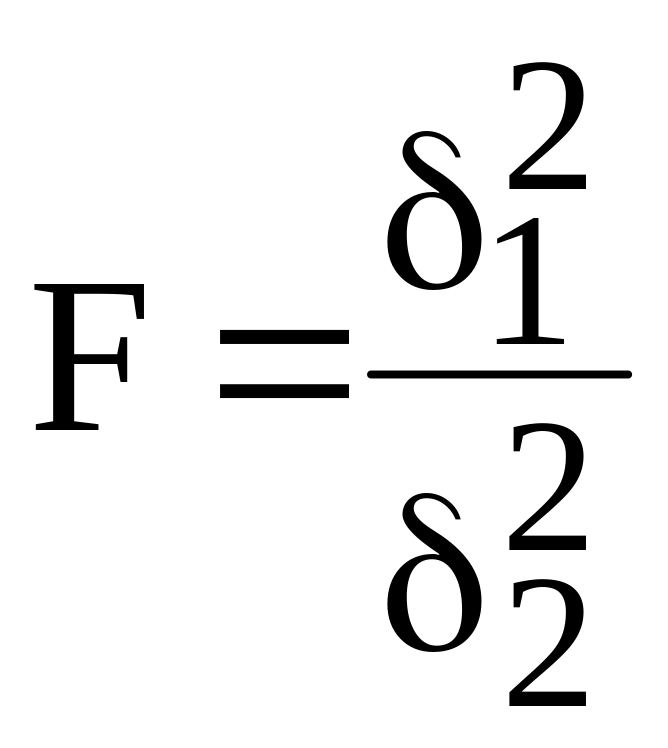, які відповідають трьом ступіням ймовірності вірогідності різноманітності: Р₁=0,999, Р₂=0,999, Р₃=0,95 при ступенях свободи _1
та₂.

100

200

500



167,5

34,1

10,1

148,5

30,8

9,6

141,1

29,5

9,3

137,1

28,5

9,1

134,6

28,2

9,0

132,9

27,9

8,9

131,8

27,7

8,9

130,0

27,5

8,8

130,0

27,4

8,8

129,5

27,2

8,8

128,9

27,1

8,8

128,3

27,1

8,7

127,7

26,9

8,7

127,1

26,8

8,7

126,5

26,7

8,7

125,9

26,6

8,7

125,6

26,5

8,6

125,3

26,4

8,6

125,0

26,4

8,6

124,7

26,3

8,5

124,4

26,2

8,5

124,1

26,2

8,5

123,8

26,1

8,5

123,5

26,1

8,5

74,1

21,2

7,7

61,2

18,8

6,9

56,1

16,7

6,6

53,4

16,0

6,4

51,7

15,5

6,3

50,5

15,2

6,2

49,8

15,0

6,1

49,0

14,8

6,0

48,6

14,7

6,0

48,2

14,7

6,0

47,8

14,5

5,9

74,4

14,4

5,9

47,0

14,2

5,9

46,0

14,1

5,8

46,2

14,0

5,8

45,8

13,9

5,8

45,6

13,9

5,8

45,4

13,7

5,7

45,2

13,7

5,7

45,0

13,6

5,7

44,7

13,5

5,7

44,5

13,5

5,7

44,3

13,5

5,6

44,1

13,5

5,6

47,0

16,3

6,6

36,6

13,3

5,8

33,2

12,1

5,4

31,1

11,4

5,2

29,8

11,0

5,1

28,8

10,7

5,0

28,2

10,5

4,9

27,6

10,3

4,8

27,3

10,2

4,8

27,0

10,1

4,7

26,7

10,0

4,7

26,7

9,9

4,7

26,4

9,8

4,6

26,1

9,7

4,6

25,8

9,6

4,6

25,4

9,5

4,5

25,1

9,4

4,5

24,9

9,3

4,5

24,6

9,2

4,4

24,5

9,1

4,4

24,3

9,1

4,4

24,1

9,1

4,4

24,0

9,0

4,4

23,8

9,0

4,4

35,5

13,4

6,0

27,0

10,9

5,1

23,7

9,8

4,8

21,9

9,2

4,5

20,8

8,8

4,4

20,0

8,5

4,3

19,5

8,3

4,2

19,0

8,1

4,1

18,8

8,0

4,1

18,5

7,9

4,1

18,3

7,8

4,0

18,0

7,7

4,0

17,7

7,6

3,9

17,5

7,5

3,9

17,2

7,4

3,8

16,9

7,3

3,8

16,8

7,2

3,8

16,6

7,1

3,8

16,5

7,1

3,7

16,4

7,0

3,7

16,2

7,0

3,7

16,1

6,9

3,7

15,9

6,9

3,7

15,9

6,9

3,7

29,2

12,3

5,6

21,7

9,6

4,7

18,8

8,5

4,4

17,2

7,9

4,1

16,2

7,5

4,0

15,5

7,2

3,9

15,1

7,0

3,8

14,6

6,8

3,7

14,4

6,7

3,7

14,2

6,6

3,8

13,9

6,5

3,6

13,7

6,4

3,6

13,5

6,3

3,5

13,2

6,2

3,5

13,0

6,1

3,4

12,7

6,0

3,4

12,6

5,9

3,4

12,5

5,9

3,3

12,3

5,9

3,3

12,2

5,8

3,3

12,1

5,8

3,3

12,0

5,7

3,3

11,8

5,7

3,2

11,7

5,7

2,2

25,4

11,3

5,3

18,5

8,7

4,6

15,8

7,6

4,1

14,4

7,0

3,8

13,5

6,6

3,7

12,9

6,4

3,6

12,6

6,2

3,5

12,0

6,0

3,4

11,8

5,9

3,4

11,6

5,8

3,3

11,4

5,7

3,1

11,2

5,7

3,3

11,0

5,6

3,2

10,8

5,5

3,2

10,5

5,4

3,2

10,3

5,3

3,1

10,2

5,2

3,1

1,01

5,1

3,1

10,0

5,1

3,0

9,9

5,0

3,0

9,7

5,0

3,0

9,6

4,9

3,0

9,5

4,9

2,9

9,4

4,9

2,9

22,9

10,6

5,1

16,4

8,0

4,8

13,9

7,0

3,6

12,6

6,4

3,6

11,7

6,1

3,5

11,1

5,8

3,4

10,8

5,6

3,3

10,4

5,5

3,2

10,2

5,4

3,2

10,0

5,3

3,1

9,8

5,2

3,1

9,6

5,1

3,1

9,4

5,0

3,0

9,2

4,9

3,0

8,9

4,8

2,9

8,7

4,7

2,9

8,6

4,6

2,9

8,5

4,5

2,8

8,4

4,5

2,8

8,3

4,4

2,8

8,1

4,4

2,8

8,0

4,4

2,7

7,9

4,3

2,7

7,9

4,3

2,7

21,0

10,0

5,0

14,9

7,9

4,1

12,3

6,6

3,7

11,3

6,0

3,5

10,5

5,6

3,3

9,9

5,4

3,2

9,6

5,2

3,1

9,2

5,1

3,1

9,0

5,0

3,0

8,9

4,9

2,9

8,7

4,8

2,9

8,5

4,7

2,9

8,3

4,6

2,8

8,1

4,5

2,8

7,8

4,4

2,7

7,6

4,3

2,7

7,5

4,3

2,7

7,4

4,2

2,6

7,3

4,1

2,6

7,2

4,1

2,6

7,1

4,0

2,6

7,0

4,0

2,6

6,9

3,9

2,6

6,8

3,9

2,5

19,7

9,7

4,8

13,8

7,2

4,0

11,6

6,2

3,6

10,4

5,7

3,4

9,6

5,3

3,2

9,1

5,1

3,1

8,8

4,9

3,0

8,4

4,7

3,0

8,2

4,6

2,9

8,0

4,5

2,9

7,8

4,5

2,8

7,6

4,4

2,8

7,4

4,3

2,7

7,3

4,2

2,7

7,1

4,1

2,7

6,9

4,0

2,6

9,8

3,9

2,6

6,7

3,9

2,6

6,6

3,8

2,5

6,5

3,7

2,5

6,3

3,7

2,5

6,2

3,7

2,4

6,1

3,6

2,4

6,0

3,6

2,4

18,6

9,3

4,8

12,3

6,9

3,9

10,8

6,0

3,5

9,6

5,4

3,3

8,9

5,1

3,1

8,4

4,8

3,0

8,1

4,7

2,9

7,7

4,5

2,9

7,5

4,4

2,8

7,4

4,3

2,8

7,2

4,2

2,7

7,0

4,2

2,7

6,8

4,1

2,6

6,7

4,0

2,6

6,5

3,9

2,5

6,3

3,8

2,5

6,2

3,7

2,5

6,1

3,6

2,4

6,0

3,6

2,4

5,9

3,5

2,4

5,7

3,5

2,4

5,6

3,4

2,3

5,5

3,4

2,3

5,4

3,4

2,3

17,8

9,1

4,7

12,3

6,7

3,8

10,2

5,7

3,4

9,1

5,2

3,2

8,4

4,9

3,0

7,9

4,6

2,9

7,6

4,4

2,8

7,2

4,3

2,8

7,0

4,2

2,7

6,9

4,1

2,7

6,7

4,0

2,6

6,5

4,0

3,6

6,3

3,9

2,6

6,2

3,8

2,5

6,0

3,7

2,5

5,8

3,6

2,4

5,7

3,6

2,4

5,6

3,4

2,3

5,5

3,4

2,3

5,4

3,3

2,3

5,3

3,3

2,3

5,2

3,2

2,2

5,1

3,2

2,2

5,0

3,2

2,2

17,1

8,9

4,6

11,8

6,5

3,7

9,7

5,6

3,3

8,6

5,0

3,1

7,9

4,7

3,0

7,4

4,5

2,9

7,1

4,3

2,8

6,8

4,1

2,7

6,6

4,0

2,7

6,5

3,9

2,6

6,3

3,9

2,6

6,1

3,8

2,5

5,9

3,7

2,5

5,8

3,6

2,4

5,6

3,5

2,4

5,4

3,4

2,4

5,3

3,3

2,3

5,2

3,3

2,3

5,1

2,2

5,0

3,1

2,2

4,9

3,1

2,2

4,8

3,1

2,2

4,7

3,0

2,1

4,6

3,0

2,1

16,6

8,7

4,5

11,3

6,4

3,7

9,3

5,4

3,3

8,3

4,9

3,1

7,6

4,6

2,9

7,1

4,3

2,8

6,8

4,1

2,7

6,5

4,0

2,6

6,3

3,9

2,6

6,2

3,8

2,6

6,0

3,7

2,5

5,8

3,6

2,5

5,6

3,5

2,4

5,5

3,4

2,4

5,3

3,3

2,3

5,1

3,2

2,3

5,0

3,2

2,3

4,9

3,1

2,2

4,8

3,1

2,2

4,7

3,0

2,2

4,6

3,0

2,1

4,5

2,9

2,1

4,4

2,9

2,1

4,3

2,9

2,1

16,1

8,5

4,5

11,0

6,2

3,6

9,0

5,3

3,2

7,9

4,8

3,0

7,3

4,4

2,9

6,8

4,2

2,7

6,5

4,0

2,7

6,2

3,9

2,6

6,1

3,8

2,5

5,9

3,7

2,5

5,8

3,6

2,5

5,6

3,5

2,4

5,4

3,5

2,4

5,3

3,4

2,3

5,1

3,3

2,3

4,9

3,2

2,2

4,8

3,1

2,2

4,7

3,0

2,2

4,6

3,0

2,1

4,5

2,9

2,1

4,4

2,9

2,1

4,3

2,8

2,0

4,2

2,8

2,0

4,1

2,8

2,0

15,7

8,4

4,5

10,7

6,1

3,6

8,7

5,2

3,2

7,7

4,7

3,0

7,0

4,3

2,8

6,6

4,1

2,7

6,3

3,9

2,6

6,0

3,8

2,6

5,8

3,7

2,5

5,7

3,6

2,5

5,5

3,5

2,4

5,3

3,5

2,4

5,1

3,4

2,3

5,0

3,3

2,3

4,8

3,2

2,2

4,6

3,1

2,2

4,5

3,0

2,2

4,4

2,9

2,1

4,3

2,9

2,1

4,3

2,8

2,0

4,2

2,8

2,0

4,1

2,7

2,0

4,0

2,7

2,0

3,9

2,7

2,0

Продовження додатка 3

100

200

500



15,4

8,3

4,4

10,4

6,0

3,5

8,5

5,1

3,2

7,5

4,6

2,9

6,8

4,2

2,8

6,4

4,0

2,7

6,1

3,8

2,6

5,8

3,7

2,5

5,0

3,6

2,7

5,5

3,5

2,4

5,3

3,4

2,4

5,1

3,4

2,3

5,0

3,3

2,3

4,8

3,2

2,2

4,7

3,1

2,2

4,5

3,0

2,1

4,4

2,9

2,1

4,3

2,8

2,1

4,2

2,8

2,0

4,1

2,7

2,0

4,0

2,7

2,0

3,9

2,6

1,9

3,8

2,6

1,9

3,7

2,6

1,9

15,1

8,2

4,4

10,2

5,9

3,5

8,3

5,0

3,1

7,3

4,5

2,9

6,6

4,2

2,7

6,2

3,9

2,6

5,9

3,8

2,5

5,6

3,6

2,5

5,5

3,5

2,4

5,8

3,4

2,4

5,2

3,4

2,3

5,0

3,3

2,3

4,8

3,2

2,3

4,7

3,1

2,2

4,5

3,0

2,1

4,4

2,9

2,1

4,2

2,9

2,1

4,1

2,8

2,0

4,0

2,7

2,0

3,9

2,7

2,0

3,8

2,6

1,9

3,7

2,5

1,9

3,6

2,5

1,9

3,5

2,5

1,9

14,8

8,1

4,3

10,0

5,8

3,5

8,1

4,9

3,1

7,1

4,4

2,9

6,5

4,1

2,7

6,0

3,9

2,6

5,7

3,7

2,5

5,4

3,6

2,4

5,3

3,4

2,4

5,1

3,4

2,3

5,0

3,3

2,3

4,8

3,2

2,3

4,7

3,1

2,2

4,5

3,0

2,2

4,4

2,9

2,1

4,2

2,9

2,1

4,1

2,8

2,0

4,1

2,7

2,0

3,9

2,6

2,0

3,8

2,6

1,9

3,7

2,5

1,9

3,6

2,5

1,9

3,5

2,4

1,8

3,4

2,4

1,8

14,6

8,0

4,3

9,8

5,8

3,5

7,9

4,9

3,1

7,0

4,4

2,8

6,3

4,0

2,7

5,9

3,8

2,6

5,6

3,6

2,5

5,3

3,5

2,4

5,2

3,4

2,4

5,0

3,3

2,3

4,9

3,2

2,3

4,7

3,2

2,2

4,5

3,1

2,2

4,4

3,0

2,1

4,2

2,9

2,1

4,0

2,8

2,0

3,9

2,7

2,0

3,8

2,6

2,0

3,7

2,6

1,9

3,6

2,5

1,9

3,6

2,5

1,9

3,5

2,4

1,8

3,4

2,4

1,8

3,4

2,4

1,8

14,4

7,9

4,3

9,6

5,7

3,4

7,8

4,8

3,0

6,8

4,3

2,8

6,2

4,0

2,7

5,8

3,8

2,6

5,5

3,6

2,5

5,2

3,4

2,4

5,1

3,3

2,4

4,9

3,3

2,3

4,8

3,2

2,3

4,6

3,1

2,2

4,4

3,0

2,2

4,3

2,9

2,1

4,1

2,8

2,1

3,9

2,7

2,0

3,8

2,7

2,0

3,7

2,6

1,9

3,6

2,5

1,9

3,6

2,5

1,8

3,5

2,4

1,8

3,4

2,4

1,8

3,3

2,3

1,8

3,2

2,3

1,8

14,2

7,9

4,3

9,5

5,7

3,4

7,7

4,8

3,0

6,7

4,8

2,8

6,1

4,0

2,6

5,6

3,7

2,5

5,4

3,5

2,4

5,1

3,4

2,4

5,0

3,3

2,3

4,8

3,2

2,3

4,7

3,1

2,2

4,5

3,1

2,2

4,3

3,0

2,1

4,2

2,9

2,1

4,0

2,8

2,0

3,8

2,7

2,0

3,7

2,6

2,0

3,6

2,5

1,9

3,5

2,5

1,9

3,5

2,4

1,8

3,4

2,4

1,8

3,3

2,3

1,8

3,2

2,3

1,8

3,1

2,3

1,8

14,0

7,8

4,3

9,3

5,6

3,4

7,6

4,7

3,0

6,6

4,2

2,8

6,0

3,9

2,6

5,6

3,7

2,5

5,3

3,5

2,4

5,0

3,4

2,4

4,9

3,2

2,3

4,7

3,2

2,3

4,6

3,1

2,2

4,4

3,0

2,2

4,2

2,9

2,1

4,1

2,8

2,1

3,9

2,7

2,0

3,7

2,7

2,5

3,6

2,6

1,9

3,5

2,5

1,9

3,4

2,4

1,9

3,4

2,4

1,8

3,3

2,3

1,8

3,2

2,3

1,8

3,1

2,2

1,7

3,0

2,2

1,7

13,9

7,8

4,2

9,2

5,6

3,4

7,5

4,7

3,0

6,5

4,2

2,8

5,9

3,9

2,6

5,5

3,6

2,5

5,2

3,5

2,4

4,9

3,3

2,3

4,8

3,2

2,3

4,6

3,1

2,2

4,5

3,0

2,2

4,3

3,0

2,0

4,2

2,9

2,1

4,0

2,8

2,1

3,9

2,7

2,0

3,7

2,6

2,0

3,6

2,5

1,9

3,5

2,4

1,9

3,4

2,4

1,8

3,3

2,3

1,8

3,2

2,3

1,8

3,1

2,2

1,7

3,0

2,2

1,7

2,9

2,2

1,7

13,7

7,7

4,2

9,1

5,5

3,4

7,4

4,6

3,0

6,4

4,1

2,7

5,8

3,8

2,6

5,4

3,6

2,5

5,1

3,4

2,4

4,8

3,3

2,3

4,7

3,2

2,3

4,5

3,1

2,2

4,4

3,0

2,2

4,2

3,0

2,1

4,1

2,9

2,1

3,9

2,8

2,0

3,8

2,7

2,0

3,6

2,6

1,9

3,5

2,5

1,9

3,4

2,4

1,8

3,3

2,4

1,8

3,2

2,3

1,8

3,1

2,3

1,8

3,0

2,2

1,7

2,9

2,1

1,7

2,8

2,1

1,7

13,6

7,7

4,2

9,0

5,5

3,3

7,3

4,6

3,0

6,3

4,1

2,7

5,7

3,8

2,6

5,3

3,6

2,5

5,1

3,4

2,4

4,8

3,3

2,3

4,7

3,1

2,2

4,5

3,1

2,2

4,4

3,0

2,2

4,2

2,9

2,1

4,0

2,8

2,1

3,9

2,7

2,0

3,7

2,6

1,9

3,5

2,5

1,9

3,4

2,5

1,9

3,3

2,4

1,8

3,2

2,3

1,8

3,2

2,2

1,8

3,1

2,2

1,7

3,0

2,2

1,7

2,9

2,1

1,7

2,8

2,1

1,7

13,5

7,6

4,2

8,9

5,4

3,3

7,2

4,6

2,9

6,3

4,1

2,7

5,7

3,8

2,6

5,2

3,5

2,4

5,0

3,4

2,4

4,7

3,2

2,3

4,6

3,1

2,2

4,4

3,0

2,2

4,3

2,9

2,1

4,1

2,9

2,1

4,0

2,8

2,1

3,8

2,7

2,0

3,7

2,6

2,0

3,5

2,5

1,9

3,4

2,4

1,9

3,3

2,3

1,8

3,2

2,3

1,8

3,1

2,2

1,7

3,0

2,2

1,7

2,9

2,1

1,7

2,8

2,1

1,7

2,7

2,1

1,6

13,4

7,6

4,2

8,9

5,4

3,3

7,1

4,5

2,9

6,2

4,0

2,7

5,6

3,7

2,5

5,2

3,5

2,4

5,0

3,3

2,3

4,7

3,2

2,3

4,6

3,1

2,2

4,4

3,0

2,2

4,3

2,9

2,1

4,1

2,9

2,1

3,0

2,8

2,0

3,8

2,7

2,0

3,6

2,6

1,9

3,4

2,5

1,9

3,3

2,4

1,8

3,2

2,3

1,8

3,1

2,3

1,7

3,0

2,2

1,7

2,9

2,1

1,7

2,8

2,1

1,7

2,7

2,1

1,6

2,6

2,0

1,6

13,3

7,6

4,2

8,8

5,4

3,3

7,1

4,5

2,9

6,1

4,0

2,7

5,5

3,7

2,5

5,1

3,5

2,4

4,9

3,3

2,3

4,6

3,2

2,3

4,5

3,1

2,2

4,3

3,0

2,2

4,2

2,9

2,1

4,0

2,8

2,1

3,9

2,7

2,0

3,7

2,7

2,0

3,6

2,5

1,9

3,4

2,5

1,9

3,3

2,4

1,8

3,2

2,4

1,8

3,1

2,2

1,8

3,0

2,2

1,7

2,9

2,1

1,7

2,8

2,1

1,7

2,7

2,0

1,6

2,6

2,0

1,6

13,2

7,5

4,1

8,7

5,3

3,3

7,0

4,5

2,9

6,0

4,0

2,7

5,4

3,7

2,5

5,0

3,4

2,4

4,8

3,2

2,3

4,5

3,1

2,2

4,4

3,0

2,2

4,2

2,9

2,1

4,1

2,9

2,1

3,9

2,8

2,1

3,8

2,7

2,0

3,7

2,6

2,0

3,5

2,4

1,9

3,4

2,4

1,9

3,2

2,3

1,8

3,2

2,2

1,8

3,1

2,2

1,7

3,0

2,1

1,7

2,8

2,1

1,7

2,7

2,0

1,6

2,6

2,0

1,6

2,5

2,0

1,6

13,1

7,4

4,1

8,6

5,3

3,3

7,0

4,4

2,9

6,0

3,9

2,7

5,4

3,6

2,5

5,0

3,4

2,4

4,8

3,2

2,3

4,5

3,1

2,2

4,4

3,0

2,2

4,2

2,9

2,1

4,1

2,8

2,1

3,9

2,8

2,1

3,8

2,7

2,0

3,6

2,6

2,0

3,5

2,5

1,9

3,3

2,4

1,9

3,2

2,3

1,8

3,1

2,2

1,8

3,0

2,2

1,7

2,9

2,1

1,7

2,8

2,1

1,7

2,6

2,0

1,6

2,6

2,0

1,6

2,5

2,0

1,6

13,0

7,4

4,1

8,6

5,2

3,3

6,9

4,4

2,9

5,9

3,9

2,6

5,3

3,6

2,5

4,9

3,3

2,4

4,7

3,2

2,3

4,4

3,0

2,2

4,3

2,9

2,1

4,1

2,9

2,1

4,0

2,8

2,1

3,8

3,7

2,0

3,7

2,6

2,0

3,6

2,5

1,9

3,4

2,4

1,9

3,3

2,3

1,8

3,4

2,3

1,8

3,1

2,2

1,7

3,0

2,1

1,7

2,9

2,0

1,6

2,7

2,0

1,6

2,6

1,9

1,6

2,5

1,9

1,6

2,4

1,9

1,5

12,9

7,3

4,1

8,5

5,2

3,2

6,8

4,3

2,8

5,8

3,9

2,6

5,3

3,5

2,5

4,9

3,3

2,3

4,7

3,1

2,3

4,4

3,0

2,2

4,3

2,9

2,1

4,1

2,8

2,1

4,0

2,7

2,1

3,8

2,7

2,0

3,7

2,6

2,0

3,5

2,5

1,9

3,4

2,4

1,9

3,2

2,3

1,8

3,1

2,2

1,8

3,0

2,1

1,7

2,9

2,1

1,7

2,8

2,0

1,6

2,7

2,0

1,6

2,8

1,9

1,6

2,5

1,9

1,5

2,4

1,8

1,5

100

200

500



12,8

7,3

4,1

8,4

5,2

3,2

6,7

4,3

2,8

5,8

3,8

2,6

5,2

3,5

2,4

4,8

3,3

2,3

4,6

3,1

2,2

4,3

3,0

2,2

4,2

2,9

2,1

4,0

2,8

2,0

3,9

2,7

2,0

3,7

2,7

2,0

3,6

2,6

1,9

3,5

2,5

1,8

3,3

2,4

1,8

3,2

2,3

1,7

3,0

2,2

1,7

3,0

2,1

1,7

2,9

2,0

1,7

2,8

2,0

1,6

2,6

1,9

1,6

2,5

1,9

1,5

2,4

1,8

1,5

2,3

1,8

1,5

17,7

7,3

4,1

8,3

5,1

3,2

6,7

4,3

2,8

5,7

3,8

2,6

5,2

3,5

2,4

4,8

3,3

2,3

4,6

3,1

2,2

4,3

3,0

2,2

4,2

2,9

2,1

4,0

2,8

2,1

3,9

2,7

2,0

3,7

2,6

2,0

3,6

2,5

1,9

3,4

2,5

1,9

3,3

2,3

1,8

3,1

2,3

1,8

3,0

2,2

1,7

2,9

2,1

1,7

2,8

2,0

1,6

2,7

1,9

1,6

2,6

1,9

1,6

2,4

1,8

1,5

2,4

1,8

1,5

2,3

1,8

1,5

12,5

7,2

4,1

8,2

5,1

3,2

6,6

4,3

2,8

5,6

3,8

2,6

5,1

3,5

2,4

4,7

3,2

2,3

4,5

3,1

2,2

4,2

2,9

2,2

4,1

2,8

2,1

3,9

2,7

2,0

3,8

2,7

2,0

3,6

2,6

2,0

3,5

2,5

1,9

3,4

2,4

1,9

3,2

2,3

1,8

3,1

2,2

1,8

2,9

2,1

1,7

2,9

2,1

1,7

2,8

2,0

1,6

2,7

1,9

1,6

2,5

1,9

1,6

2,4

1,8

1,5

2,3

1,8

1,5

2,2

1,7

1,5

12,4

7,2

4,0

8,1

5,1

3,2

6,5

4,2

2,8

5,6

3,8

2,6

5,0

3,4

2,4

4,6

3,2

2,3

4,4

3,0

2,2

4,1

2,9

2,1

4,0

2,8

2,1

3,8

2,7

2,0

3,7

2,6

2,0

3,5

2,6

2,0

3,4

2,5

1,9

3,3

2,4

1,9

3,1

2,3

1,8

3,0

2,2

1,7

2,8

2,1

1,7

2,8

2,0

1,5

2,7

2,0

1,6

2,6

1,9

1,6

2,4

1,9

1,5

2,3

1,8

1,5

2,2

1,8

1,5

2,1

1,7

1,5

12,3

7,2

4,0

8,1

5,1

3,2

6,4

4,2

2,8

5,5

3,7

2,6

5,0

3,4

2,4

4,6

3,2

2,3

4,4

3,0

2,2

4,1

2,8

2,1

4,0

2,8

2,1

3,8

2,7

2,0

3,7

2,6

2,0

3,5

2,6

2,0

3,4

2,5

1,9

3,3

2,4

1,9

3,1

2,3

1,8

3,0

2,2

1,7

2,8

2,1

1,7

2,8

2,0

1,6

2,7

1,9

1,6

2,6

1,8

1,6

2,4

1,8

2,3

1,8

1,5

2,2

1,7

1,5

2,1

1,7

1,4

12,2

7,2

4,0

8,0

5,1

3,2

6,4

4,2

2,8

5,4

3,7

2,6

4,9

3,4

2,4

4,5

3,2

2,3

4,3

3,0

2,2

4,0

2,9

2,1

3,9

2,8

2,1

3,7

2,7

2,0

3,6

2,6

2,0

3,4

2,6

1,9

3,8

2,5

1,9

3,2

2,4

1,8

3,0

2,3

1,8

2,9

2,2

1,7

2,7

2,1

1,7

2,7

2,0

1,6

2,6

1,9

1,6

2,5

1,9

1,5

2,3

1,8

1,5

2,2

1,8

1,5

2,1

1,7

1,5

2,0

1,7

1,4

12,1

7,1

4,0

7,9

5,0

3,2

6,3

4,1

2,8

5,4

3,7

2,5

4,9

3,4

2,4

4,5

3,1

2,3

4,3

3,0

2,2

4,0

2,8

2,1

3,9

2,7

2,0

3,7

2,7

2,0

3,6

2,6

2,0

3,4

2,5

1,9

3,3

2,4

1,9

3,2

2,3

1,8

3,0

2,2

1,8

2,9

2,1

1,7

2,7

2,1

1,7

2,7

2,0

1,6

2,6

1,9

1,6

2,5

1,8

1,5

2,3

1,8

1,5

2,2

1,7

1,5

2,1

1,7

1,4

2,0

1,6

1,4

12,0

7,1

4,0

7,8

5,0

3,1

6,2

4,1

2,8

5,3

3,6

2,5

4,8

3,3

2,4

4,4

3,1

2,2

4,2

2,9

2,2

3,9

2,8

2,1

3,8

2,7

2,0

3,6

2,6

2,0

3,5

2,6

1,9

3,3

2,5

1,9

3,2

2,4

1,9

3,1

2,3

1,8

2,9

2,2

1,7

2,8

2,1

1,7

2,6

2,0

1,6

2,6

1,9

1,6

2,5

1,9

1,6

2,4

1,8

1,6

2,2

1,7

1,5

2,1

1,7

1,4

2,0

1,6

1,4

1,9

1,6

1,4

11,9

7,0

4,0

7,7

5,0

3,1

6,1

4,1

2,7

5,2

3,6

2,5

4,7

3,3

2,4

4,3

3,1

2,2

4,1

2,9

2,1

3,8

2,8

2,1

3,7

2,7

2,0

3,5

2,6

2,0

3,4

2,5

1,9

3,2

2,5

1,9

3,1

2,4

1,8

3,0

2,3

1,8

2,8

2,2

1,7

2,7

2,1

1,7

2,5

2,0

1,6

2,5

1,9

1,6

2,4

1,8

1,5

2,3

1,8

1,5

2,1

1,7

1,5

2,0

1,7

1,5

1,9

1,6

1,4

1,8

1,6

1,4

11,6

7,0

4,0

7,6

4,9

3,1

6,0

4,1

2,7

5,2

3,6

2,5

4,7

3,3

2,3

4,3

3,1

2,2

4,1

2,9

2,1

3,8

2,8

2,1

3,7

2,7

2,0

3,5

2,6

2,0

3,4

2,5

1,9

3,2

2,4

1,9

3,1

2,3

1,8

3,0

2,3

1,8

2,8

2,1

1,7

2,7

2,1

1,7

2,5

2,0

1,6

2,4

1,9

1,6

2,3

1,8

1,5

2,2

1,7

1,5

2,1

1,7

1,4

2,0

1,6

1,4

1,8

1,6

1,4

1,7

1,6

1,3

11,6

7,0

4,0

7,5

4,9

3,1

6,0

4,0

2,7

5,1

3,6

2,5

4,6

3,2

2,3

4,2

3,0

2,2

4,0

2,9

2,1

3,7

2,7

2,0

3,6

2,6

2,0

3,4

2,5

1,9

3,3

2,5

1,9

3,1

2,4

1,9

3,0

2,3

1,8

2,9

2,2

1,8

2,7

2,1

1,7

2,6

2,0

1,6

2,4

1,9

1,6

2,4

1,8

1,5

2,3

1,8

1,5

2,2

1,7

1,4

2,0

1,6

1,4

1,9

1,6

1,4

1,8

1,5

1,3

1,7

1,5

1,3

100

11,5

6,9

3,9

7,4

4,9

3,1

5,9

4,0

2,7

5,0

3,5

2,5

4,5

3,2

2,3

4,1

3,0

2,2

3,9

2,8

2,1

3,7

2,7

2,0

3,6

2,6

2,0

3,4

2,5

1,9

3,3

2,4

1,9

3,1

2,4

1,8

3,0

2,3

1,8

2,8

2,2

1,7

2,7

2,1

1,7

2,5

2,0

1,6

2,4

1,9

1,6

2,3

1,8

1,5

2,2

1,7

1,5

2,1

1,6

1,4

1,9

1,6

1,4

1,8

1,5

1,3

1,7

1,5

1,3

1,6

1,4

1,3

125

11,4

6,8

3,9

7,4

4,8

3,1

5,8

3,9

2,7

5,0

3,5

2,4

4,5

3,2

2,3

4,1

2,9

2,2

3,9

2,8

2,1

3,6

2,6

2,0

3,5

2,6

1,9

3,3

2,5

1,9

3,2

2,4

1,9

3,0

2,3

1,8

3,9

2,2

1,8

2,8

2,1

1,7

2,6

2,0

1,6

2,5

1,9

1,6

2,3

1,8

1,5

2,3

1,7

1,5

2,1

1,7

1,4

2,0

1,6

1,4

1,9

1,5

1,4

1,8

1,5

1,3

1,6

1,4

1,3

1,5

1,4

1,2

150

11,3

6,8

3,9

7,3

4,7

3,1

5,7

3,9

2,7

4,9

3,4

2,4

4,4

3,1

2,3

4,0

2,9

2,2

3,8

2,8

2,1

3,5

2,6

2,0

3,4

2,5

1,9

3,2

2,4

1,9

3,1

2,4

1,8

2,9

2,3

1,8

2,8

2,2

1,8

2,7

2,1

1,7

2,5

2,0

1,6

2,4

1,9

1,6

2,2

1,8

1,5

2,2

1,7

1,5

2,0

1,7

1,4

1,9

1,6

1,4

1,8

1,5

1,3

1,7

1,4

1,3

1,5

1,4

1,2

1,4

1,3

1,2

200

11,2

6,8

3,9

7,3

4,7

3,0

5,6

3,9

2,6

4,8

3,4

2,4

4,3

3,2

2,3

3,9

2,9

2,1

3,7

2,7

2,0

3,5

2,6

2,0

3,4

2,5

2,0

3,4

2,5

1,9

3,2

2,4

1,9

3,1

2,3

1,8

2,9

2,3

1,8

2,8

2,2

1,7

2,6

2,1

1,7

2,5

2,0

1,6

2,3

1,9

1,6

2,2

1,8

1,5

2,1

1,7

1,4

1,9

1,6

1,4

1,8

1,5

1,3

1,7

1,5

1,3

1,6

1,4

1,3

1,2

400

11,0

6,7

3,9

7,1

4,7

3,0

5,6

3,8

2,6

4,7

3,4

2,4

4,2

3,1

2,2

3,8

2,8

2,1

3,6

2,7

2,0

3,4

2,5

2,0

3,3

2,5

1,9

3,1

2,4

1,8

3,0

2,3

1,8

2,8

2,2

1,8

2,7

2,1

1,7

2,5

2,0

1,7

2,4

1,9

1,6

2,2

1,8

1,5

2,1

1,7

1,4

2,0

1,6

1,4

1,9

1,6

1,4

1,8

1,5

1,3

1,6

1,4

1,3

1,5

1,3

1,2

1,4

1,2

1,3

1,2

1,1

1000

10,9

6,7

3,8

7,0

4,6

3,0

5,5

3,8

2,6

4,7

3,4

2,4

4,2

3,3

2,2

3,8

3,0

2,1

3,6

2,8

2,0

3,4

2,7

1,9

3,3

2,5

1,9

3,1

2,4

1,8

3,0

2,3

1,8

2,8

2,3

1,8

2,7

2,2

1,7

2,5

2,1

1,6

2,4

2,0

1,6

2,2

1,9

1,5

2,1

1,8

1,5

2,0

1,7

1,4

1,8

1,6

1,4

1,7

1,5

1,3

1,6

1,4

1,3

1,5

1,4

1,2

1,3

1,2

1,1

1,2

1,1



10,8

6,6

3,8

6,9

4,6

3,0

5,4

3,8

2,6

4,6

3,3

2,4

4,1

3,0

2,2

3,7

2,8

2,1

3,5

2,6

2,0

3,3

2,5

1,9

3,2

2,4

1,9

3,0

2,3

1,8

2,9

2,2

1,8

2,7

2,2

1,7

2,6

2,1

1,7

2,4

2,0

1,6

2,3

1,9

1,6

2,1

1,8

1,5

2,0

1,7

1,5

1,9

1,6

1,4

1,7

1,5

1,3

1,6

1,4

1,3

1,5

1,4

1,2

1,4

1,2

1,1

1,0

Додаток 4.

Число ступенів свободи 	Ймовірність (Р)			Число ступенів свободи 	Ймовірність (Р)
	0,95	0,99	0,999		0,95	0,99	0,999
значення хі-квадрат
1	3,9	6,6	10,8	26	38,9	45,6	54,1
2	6,0	9,2	13,8	27	40,1	47,0	55,5
3	7,8	11,3	16,3	28	41,3	48,3	56,3
4	9,5	13,3	18,5	29	42,6	49,6	58,3
5	11,1	15,1	20,5	30	43,8	50,9	59,7
6	12,6	16,8	22,5	32	46,2	53,5	62,4
7	14,1	18,5	24,3	34	48,6	56,0	65,2
8	15,5	20,1	26,1	36	51,0	58,6	67,9
9	16,9	21,7	27,9	38	53,4	61,1	70,7
10	18,3	23,2	29,6	40	55,8	63,7	73,4
11	19,7	24,7	31,3	42	58,1	66,2	76,1
12	21,0	26,2	32,9	44	60,5	68,7	78,7
13	22,4	24,7	34,5	46	62,8	71,2	81,4
14	23,7	29,1	36,1	48	65,2	73,7	84,0
15	25,0	30,6	37,7	50	67,5	76,2	86,7
16	26,3	32,0	39,3	55	73,3	82,3	93,2
17	27,6	33,4	40,8	60	79,1	88,4	99,6
18	28,9	34,8	42,3	65	89,8	94,4	106,0
19	30,1	36,2	43,8	70	90,5	100,4	112,3
20	31,4	37,6	45,3	75	96,2	160,4	118,5
21	32,7	38,9	46,8	80	101,9	112,3	124,8
22	33,9	40,3	48,3	85	107,5	118,2	131,0
23	35,2	41,6	49,7	90	113,1	124,1	137,1
24	36,4	43,0	51,2	95	118,7	130,0	143,3
25	37,7	44,3	52,6	100	124,3	135,8	149,4

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1010

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.07.2025373.25 Кб0Metodichni_vkazivki_dlya_vikonannya_kursovogo_p...doc
#
01.05.2025225.79 Кб0Metodi_kontrolyu.doc
#
01.03.2025184.83 Кб0Metod_po_kursoviy_OEVS.doc
#
15.04.2019340.48 Кб3Metod_rekomend_Sobivart_Zi_zminami_2009_1.doc
#
01.07.2025912.38 Кб0met_mod_N.doc
#
01.07.20251.65 Mб0Met_ZOO_excel2013.doc
#
10.11.20193.52 Mб24Mim_rob.doc
#
01.07.20251.15 Mб0Ministerstvo_agrarnoyi_politiki_ta_prodovolstva...docx
#
11.09.2019500.74 Кб3Mizhnar_ekonom (1).doc
#
01.07.202532.94 Кб0Modul_mova.docx
#
01.07.2025553.47 Кб0Moloko.doc