Методические указания и рекомендации для выполнения
практических работ по дисциплине
«Надежность и отработка КА»
Занятие №1
Законы распределения случайных величин
Задание
1. Построить графики плотности распределения для различных законов распределения времени безотказной работы:
1.1. нормальный закон распределения;
1.2. закон распределения Релея;
1.3. закон распределения Вейбулла;
1.4. усеченного нормального закона распределения
1.5. логарифмически нормальный закон распределения.;
1.6. закона распределения Эрланга.
Основные расчетные соотношения (типовые законы распределения)
1.
; Экспоненциальный
2.
; Релея
3.
;
Нормальный
4.
;
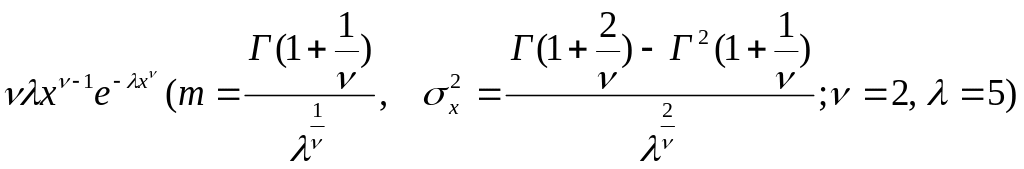Вейбулла
5.
;
Логарифмически-нормальный
6.
(
) ; Эрланга
Пример выполнения задания № 1.1
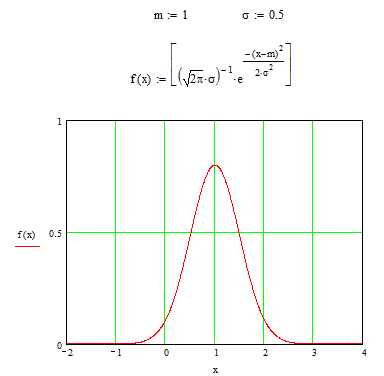
Рис. 1.1 Плотность нормального закона распределения.
2.
Подобрать законы распределения для
различных выборок представленных в
табл. 1.1 по критерию согласия Пирсона
--
.
Распределение
числа попаданий
результатов измерений в интервалы
Таблица 1.1
N |
|
1 |
2 |
3 |
4 |
1 |
0—0.25 |
68 |
19 |
1 |
28 |
2 |
0.25—0.5 |
21 |
35 |
3 |
46 |
3 |
0.5—0.75 |
7.5 |
28 |
24 |
22 |
4 |
0.75--1 |
2.5 |
13 |
45 |
3 |
5 |
1—1.25 |
1 |
2 |
24 |
1 |
6 |
1.25—1.5 |
0 |
1 |
3 |
0 |
7 |
1.5—1.75 |
0 |
0 |
0 |
0 |
8 |
1.75--2 |
0 |
0 |
0 |
0 |
N |
|
5 |
6 |
1 |
0—1.5 |
5 |
24 |
2 |
1.5--3 |
47 |
31 |
3 |
3—4.5 |
27 |
21 |
4 |
4.5--6 |
12 |
12 |
5 |
6—7.5 |
6 |
6 |
6 |
7.5--9 |
2 |
3 |
7 |
9—10.5 |
1 |
2 |
8 |
10.5--12 |
0 |
1 |
Основные расчетные соотношения
Оценка математического ожидания и дисперсии(средне-квадратического отклонения):
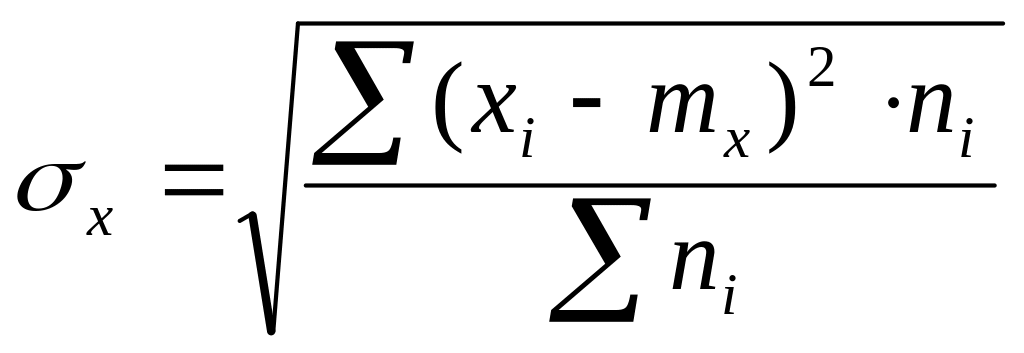
Расчет
выравнивающих частот
Вычисление
Квантили
распределения
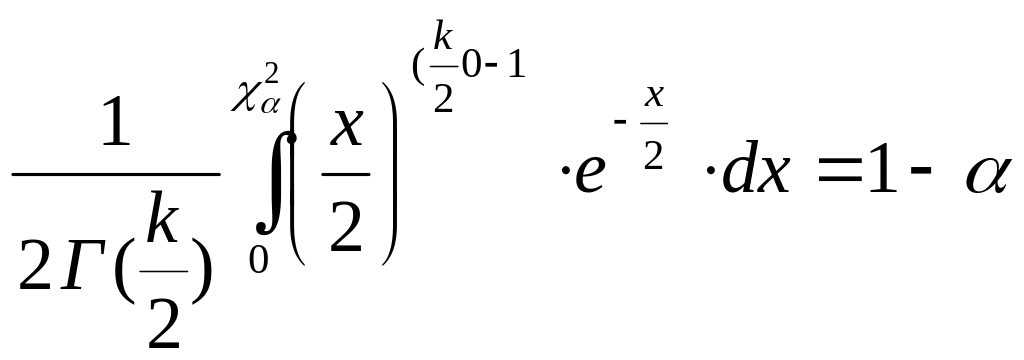
Таблица 2.1
k |
|
||||||||||||
0,99 |
0,98 |
0,95 |
0,90 |
0,8 |
0,7 |
0,50 |
0,3 |
0,20 |
0,10 |
0,05 |
0,02 |
0,01 |
|
1 |
0 |
0,001 |
0,004 |
0,02 |
0,06 |
0,15 |
0,45 |
1,07 |
1,64 |
2,71 |
3,84 |
5,41 |
6,64 |
2 |
0,02 |
0,04 |
0,10 |
0,21 |
0,45 |
0,71 |
1,38 |
2,41 |
3,22 |
4,60 |
5,99 |
7,82 |
9,21 |
3 |
0,11 |
0,18 |
0,35 |
0,58 |
1,00 |
1,42 |
2,37 |
3,66 |
4,64 |
6,25 |
7,82 |
9,84 |
11,34 |
4 |
0,30 |
0,43 |
0,71 |
1,06 |
1,65 |
2,20 |
3,36 |
4,88 |
5,99 |
7,78 |
9,49 |
11,67 |
13,28 |
5 |
0,55 |
0,75 |
1,14 |
1,61 |
2,34 |
3,00 |
4,35 |
6,06 |
7,29 |
9,24 |
11,1 |
13,39 |
15,09 |
6 |
0,87 |
1,13 |
1,63 |
2,20 |
3,07 |
3,83 |
5,35 |
7,23 |
8,56 |
10,6 |
13,0 |
15,03 |
16,81 |
7 |
1,24 |
1,56 |
2,17 |
2,83 |
3,82 |
4,67 |
6,35 |
8,38 |
9,80 |
12,0 |
15,0 |
16,62 |
18,48 |
8 |
1,64 |
2,03 |
2,73 |
3,49 |
4,59 |
5,53 |
7,34 |
9,52 |
11,0 |
13,4 |
15,5 |
18,17 |
20,10 |
9 |
2,09 |
2,53 |
3,32 |
4,17 |
5,38 |
6,39 |
8,34 |
10,7 |
12,2 |
14,7 |
16,9 |
19,68 |
21,70 |
10 |
2,56 |
3,06 |
3,94 |
4,86 |
6,18 |
7,27 |
9,34 |
11,8 |
13,4 |
16,0 |
18,3 |
21,20 |
23,20 |
11 |
3,05 |
3,61 |
4,58 |
5,58 |
6,99 |
8,15 |
10,3 |
12,9 |
14,6 |
17,3 |
19,7 |
22,60 |
24,70 |
12 |
3,57 |
4,18 |
5,23 |
6,30 |
7,81 |
9,03 |
11,3 |
14,0 |
15,8 |
18,5 |
21,0 |
24,10 |
26,20 |
13 |
4,11 |
4,76 |
5,89 |
7,04 |
8,63 |
9,93 |
12,3 |
15,1 |
17,0 |
19,8 |
22,4 |
25,50 |
27,70 |
Пример выполнения задания 2.1
(проверяем экспоненциальный закон распределения)
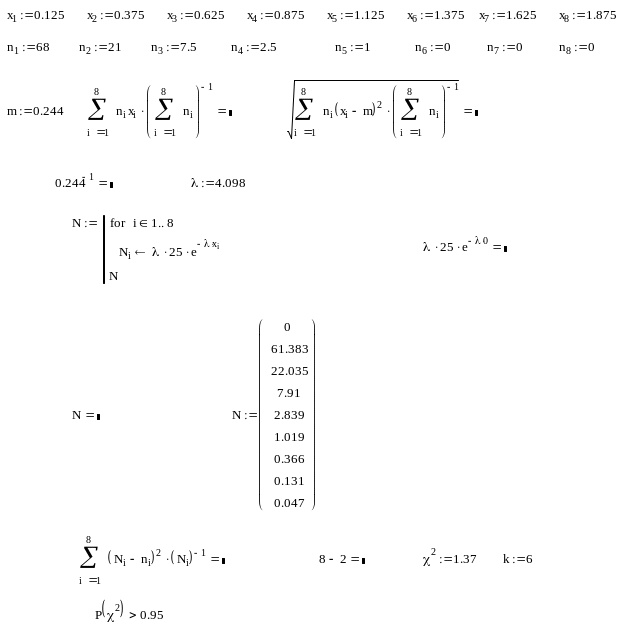
Занятие №2
Расчет надежности элемента.
Задание
1. Записать выражение для интенсивностей отказа различных законов распределения:
1.1 нормального; 1.2 Релея; 1.3 Вейбулла.
Основные расчетные соотношения
Интенсивность отказа рассчитывается по соотношению:
,
где
функция
надежности;
случайная
величина
Пример выполнения задания №1.1
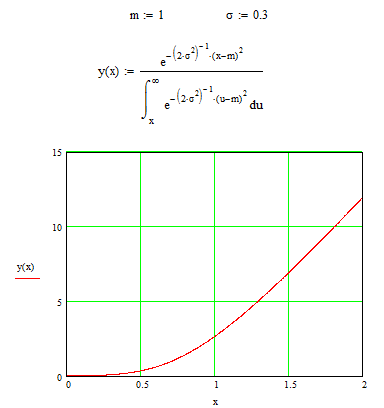
Рис. 2.1 Интенсивность отказа, соответствующая нормальному закону распределения.
2. Рассчитать надежность:
2.1 обечайки , нагруженной растягивающими усилиями
(
исходные данные:
атм.;
1,5;
1,14
т/м; R=2
м; h=3м
;
320
МПа ;
3мм;
5%
;
5%
;
2%
;
3%).
2.2 раскрытия поворотной штанги антенны.
(исходные
данные:
;
;
,
где N—работа движущих сил; R – работа сил сопротивления).
2.3 безударного разделения блоков.
(исходные
данные:
мм
;
мм.
минимальное
расстояние между опасными точками
разделяемых блоков)
2.4 обечайки , нагруженной сжимающими усилиями
(
исходные данные:
;
мм;
k=0,2,
m==0,125;
n=0,25;
N=200
Кн,
Кн,
Кн;
)
Законы распределения случайных параметров во всех заданиях считать нормальными.