2) Когда условия опыта не одинаковы, величину y определяют в каждом опыте, а ее среднее значение подсчитывают по формуле

.

Абсолютная ошибка величины Y определяется соотношением

,

где Y_A,  Y_B,  Y_C , ... – частные абсолютные ошибки, обусловленные ошибками измерений величин A, B, С,... Частные абсолютные ошибки представляют собой приращения Y , вызванные соответствующими приращениями величин А, В, С,... на величину абсолютной ошибки  А,  B,  С, ...

……………………………………………………..

С математической точки зрения величина Y = f (А, В, С,...) является функцией нескольких переменных, а величины Y_A, Y_B, Y_C, … представляют собой частные дифференциалы, которые могут быть вычислены по формулам

, , , …

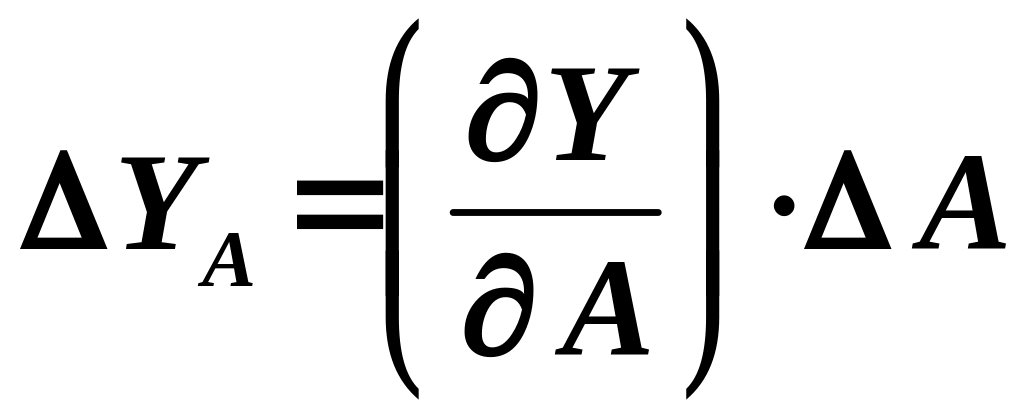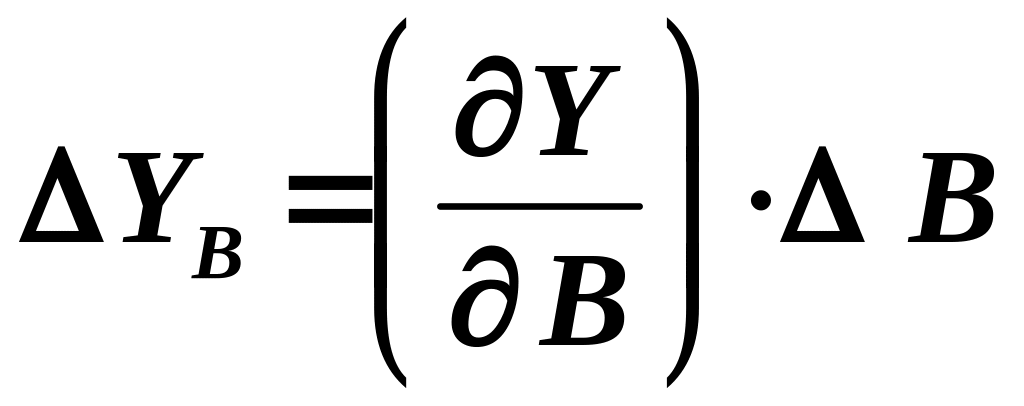Здесь – частные производные по переменным A, B, C и т.д.

С учетом этого формула для абсолютной ошибки Y может быть представлена в виде

.

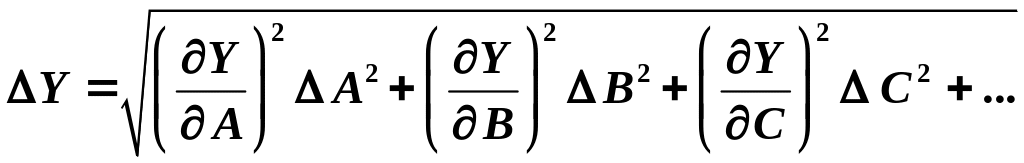В ряде случаев для расчета Y можно получить сравнительно простые соотношения. Некоторые из них можно найти в таблицах.

Процесс обработки результатов косвенных измерений можно представить в виде следующего алгоритма.

1. Провести необходимое число однотипных опытов при одинаковых условиях и оценить среднее значение каждой из измеряемых величин А, В, С,... и их абсолютные ошибки А, B, С, …

2. Подсчитать среднее значение искомой величины по формуле

.

3. Определить абсолютную ошибку Y по формуле

, в которой

, ;

, ;

, ;

4. Окончательный результат измерений представить в виде

.

5. Определить относительную ошибку полученного результата

.

1. При неодинаковых условиях опытов среднее значение определить по формуле

,

где Y₁, Y₂, Y₃, ... – значения Y, полученные в отдельных опытах. В этом случае обработку результатов измерений проводить по правилам обработки прямых измерений.

Примечание. Обработку результатов косвенных измерений следует проводить с помощью компьютера, например в редакторе EXCEL по Программе 2, прилагаемой к практикуму.

3. Обработка результатов измерений методом наименьших квадратов

С помощью опытов часто приходится изучать зависимость одной физической величины от другой. Эта зависимость может быть представлена таблицей, графиком или формулой.

Во многих случаях зависимость величин друг от друга путем замены переменных может быть сведена к линейной зависимости вида

Такая операция называется линеаризацией функции.

Будем полагать, что линеаризация проведена, и что теперь некоторая величина y линейно зависит от x.

Пусть проведено n опытов и в каждом опыте получена пара значений (x_i , y_i ). По этим n парам значений x и y необходимо найти коэффициенты k и b линейного уравнения. Экспериментальные значения (x_i, y_i) на графике будут группироваться вблизи некоторой прямой.

Р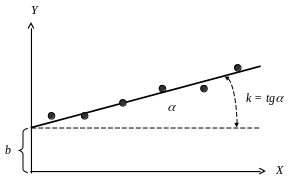 ис.

Отклонение каждого значения y от прямой характеризуется величиной d.

Основной задачей метода наименьших квадратов является поиск наилучшей прямой, для которой сумма квадратов этих отклонений будет минимальной

.

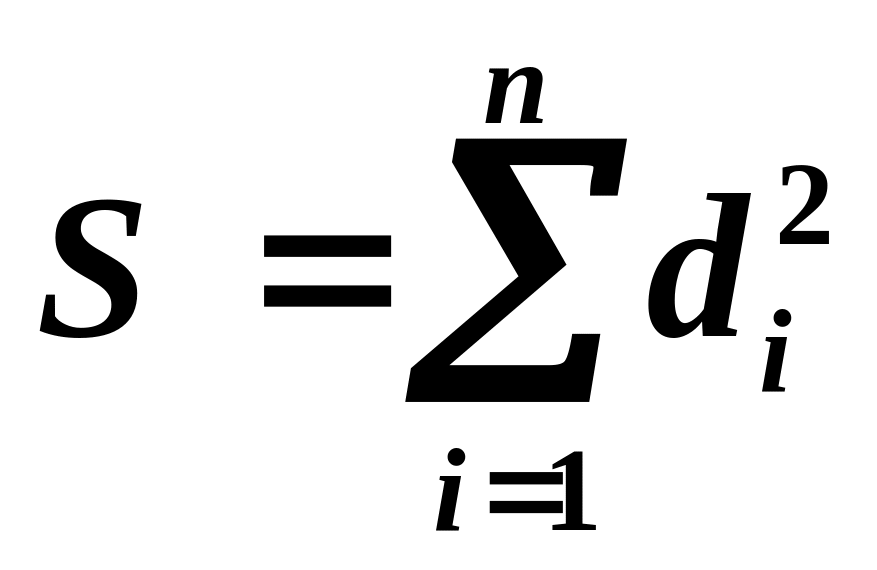Условие минимума S приводит к равенству нулю производных от S по k и b:

;

.

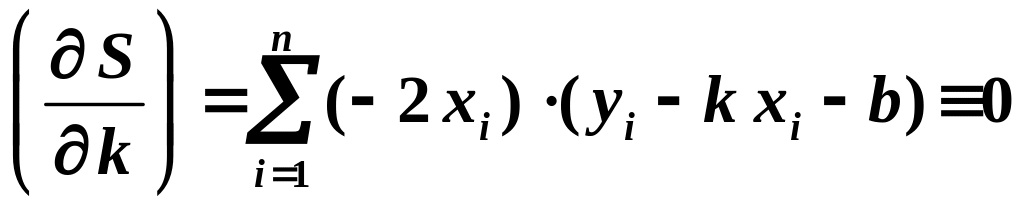Решение приведенной системы уравнений позволяет получить формулы для расчета наилучших значений k и b:

, .

Расчет среднеквадратичных отклонений проводят по формулам

; ,

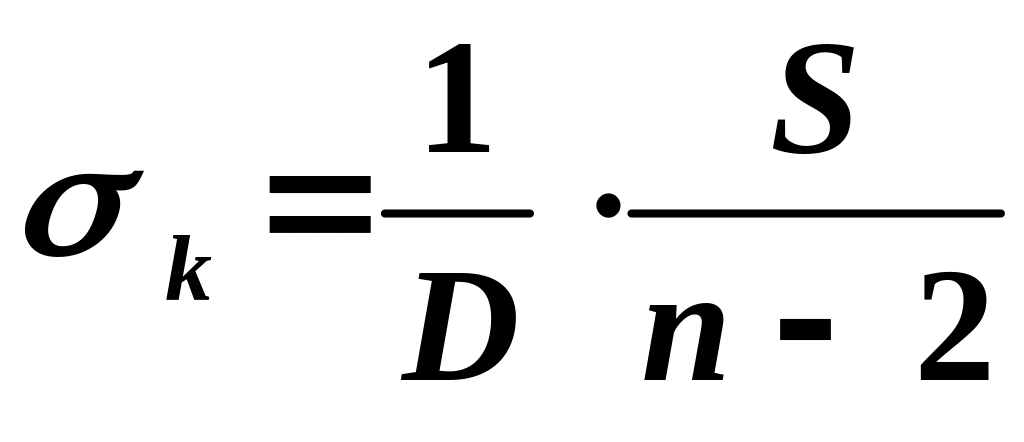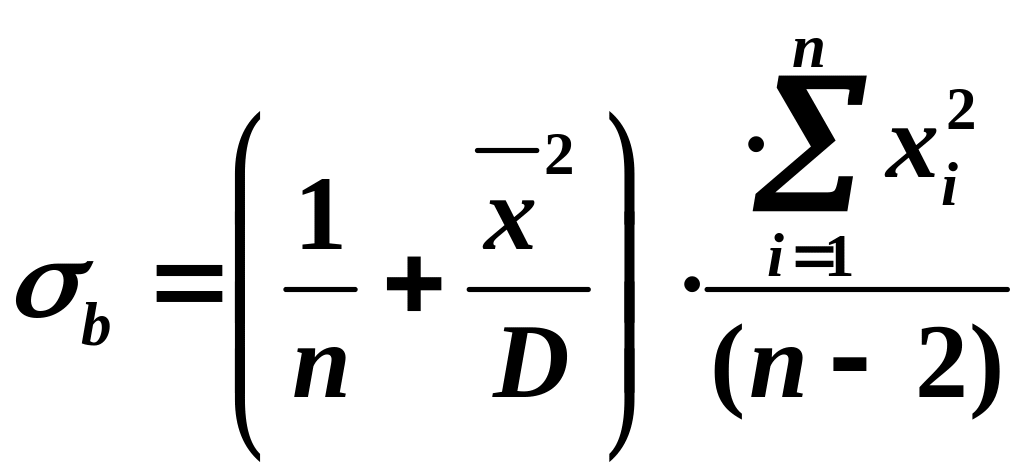в которых

, .

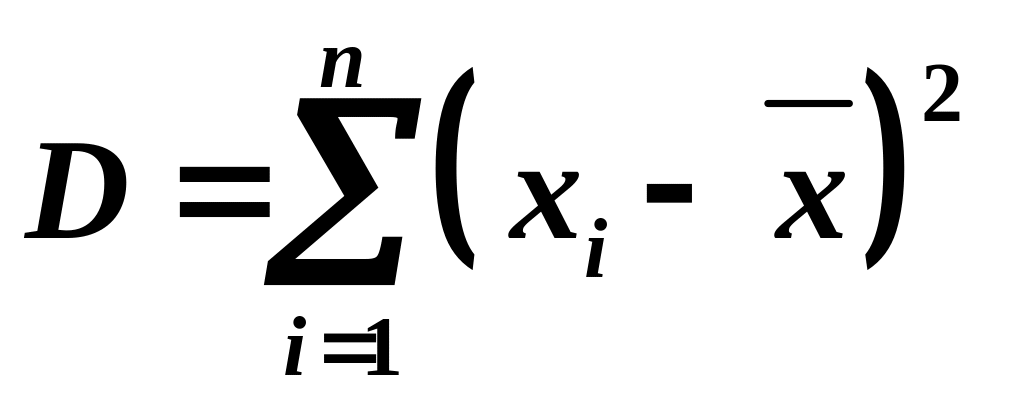При заданной надежности (р = 0,95) коэффициенты Стьюдента определяют из таблицы 1 для (n – 1) и абсолютные ошибки  k и  b рассчитывают по формулам

 k = t (p, n – 1) _k ,  b = t (p, n – 1) _b.

Здесь n – число пар значений (x_i, y_i). Окончательный результат представляют в виде

, .

Примечание. Обработку результатов измерений следует провести методом наименьших квадратов с помощью компьютера, например в редакторе EXCEL по Программе 3, прилагаемой к практикуму.