Группа 21 – 2014/15

1. Алистратова Анна

2. Алябьева Юлия

3. Богатырев Андрей

4. Голикова Елена

5. Есенкова Светлана

6. Затолокина Юлия

7. Ишкова Светлана

8. Каширина Татьяна

9. Левина Светлана

10. Меркелова Юлия

11. Наумова Анастасия

Обработка результатов измерений

При измерении узнают во сколько раз измеряемая физическая величина больше или меньше величины, принятой за единицу измерения.

По способу получения числового результата различают прямые и косвенные измерения.

При прямых измерениях значение искомой величины получают непосредственно с помощью меры или измерительного прибора.

При косвенных измерениях значение измеряемой величины находят по известной формуле, в которую входят непосредственно измеряемые величины.

Следует помнить, что никакие измерения нельзя выполнить абсолютно точно. Результаты измерений всегда содержат ошибку. Поэтому в задачу измерений входят: 1) Нахождение наиболее вероятного значения искомой величины, 2) Оценка допущенной при измерении ошибки (погрешности).

Ошибка измерений характеризует отклонение результата измерений от истинного значения искомой величины. По способу представления различают абсолютную и относительную ошибки.

Абсолютная ошибка выражается в единицах измеряемой величины

 x = X – x.

Здесь X – истинное значение измеряемой величины (неизвестная величина), x – результат одного из измерений,  x – абсолютная ошибка измерения.

Относительная ошибка выражается в долях или процентах от истинного значения измеряемой величины

.

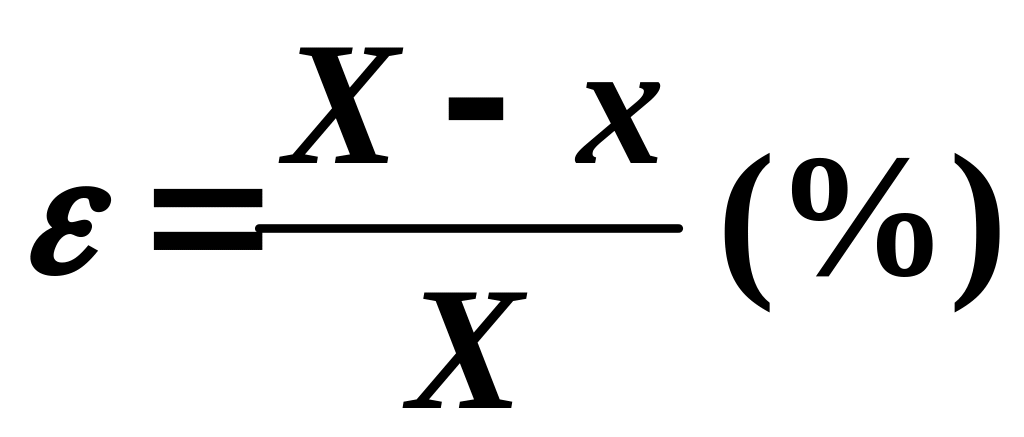Различают систематические и случайные ошибки и грубые ошибки – промахи.

Чтобы не допускать грубых ошибок, нужно быть внимательным и аккуратным.

Систематические ошибки – это ошибки, которые остаются постоянными или закономерно изменяются в процессе измерений.

Назовем некоторые причины их возникновения.

1. Условия эксперимента не совпадают с предполагаемыми условиями измерений, например, неравноплечие весов, тепловое расширение линейки, действие на взвешиваемые тела архимедовой силы и т.д. Эти ошибки можно выявить при анализе условий измерения и устранить путем введения соответствующей поправки.

2. Исследуемый объект обладает некоторыми, неизвестными экспериментатору особенностями. Например, объект имеет внутренние полости (пустоты, раковины), неоднородную структуру, несовершенную геометрическую форму и т.п. Для выявления подобных ошибок необходимо проводить многократные измерения в разных условиях, используя разные объекты и методы.

3. Неточность измерительных приборов приводит к появлению систематической ошибки, обусловленной их классом точности. Эту ошибку называют инструментальной.

Класс точности всегда указывается в паспорте прибора (0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0). Он определяется отношением максимальной абсолютной ошибки к предельному значению шкалы прибора.

Например, шкала амперметра рассчитана на токи от 0 до 5 A и его класс точности 1,0. Это значит, что абсолютная ошибка прибора составляет 1% от 5 А:

 I = 0,015 A = 0,05 A.

Обычно цену деления прибора согласуют с его классом точности. Поэтому в качестве предельной абсолютной инструментальной ошибки будем принимать цену наименьшего деления шкалы прибора:

.

Случайные ошибки –вызываются целым рядом случайных причин. Они непрерывно изменяются непредсказуемым образом.

Случайные ошибки всегда присутствуют в измерениях и с одинаковой вероятностью принимают как положительные, так и отрицательные значения.

На рис. 1 представлена схема,  характеризующая разброс экспериментальных значений измеряемой величины по отношению к истинному значению.

Присутствие систематической ошибки приводит к некоторому постоянному смещению значений   x_i от истинного значения (рис. 2).

Случайные ошибки устранить нельзя, но их можно оценить, используя методы математической статистики.

Если известны величины случайной и систематической ошибок, то общая абсолютная ошибка определится по формуле

.

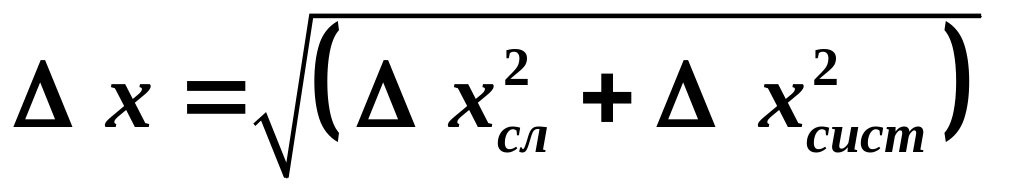Приведенная формула предполагает независимость ошибок друг от друга.

Абсолютная ошибка x определяет полуширину интервала, которому принадлежит истинное значение измеряемой величины с заданной  надежностью   p . Этот   интервал   называют доверительным­ интервалом, а величину p называют надежностью или доверительной вероятностью. В лабораторной практике результаты измерений принято представлять с надежностью 95% (p = 0,95).

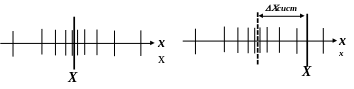
Рис. 1 Рис. 2