Розділ 1 проектування елементарних геометричних фігур

Побудова проекцій геометричних елементів ґрунтується на методі ортогонального паралельного проектування. В ортогональному проектуванні знаходять кілька проекцій оригіналу на взаємно перпендикулярні площини проекцій (рис. 1.1)

а) б)

Рисунок 1.1 – Ортогональна система двох (а) та трьох (б) площин проекцій

Дві площини проекцій ділять весь простір на чотири двогранні кути, які називають квадранти або чверті.

Три координатні площини проекцій ділять весь простір на вісім тригранних кутів, які називають октантами. Знаки координат в октантах представлені в таблиці 1.1.

Таблиця 1.1 – Знаки координат

Октанти	Координати			Октанти	Координати
	Х	Y	Z		Х	Y	Z
І ІІ ІІІ ІV	+ + + +	+ - - +	+ + - -	V VI VII VIII	- - - -	+ - - +	+ + - -

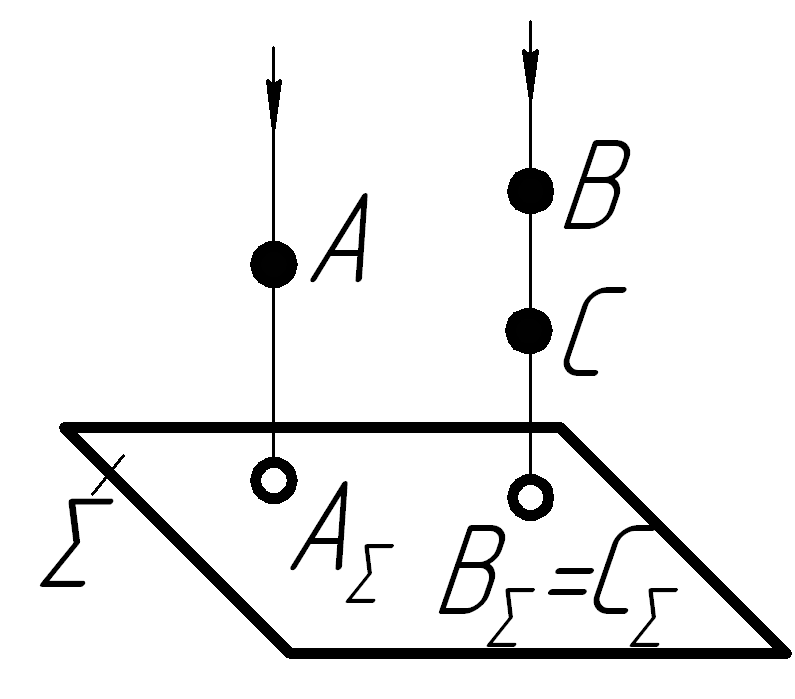
Основні положення проекції точки:

1. прямокутною проекцією точки є основа перпендикуляра, який опущений з даної точки на площину проекцій (рис.1.2);

2. проекцією точки завжди буде точка;

3. кожна точка має тільки одну проекцію на даній площині проекцій;

4. д

   Рисунок 1.2 ─ Ортогональне проектування точки на площину проекцій

   ві точки, розміщені на одному проекційному промені, проектуються в одну точку (рис.1.2).

Одна проекція точки не визначає її положення в просторі відносно площин проекцій, тоді як дві проекції точки визначають положення самої точки відносно площин проекцій.

1.1 Проекція точки на дві площини проекцій, епюр точки

Множина двох (або більше) ортогональних проекцій точки (після суміщення площин проекцій) називається епюром (від французького epure – креслення). Більш загальне визначення епюра: зображення, яке отримуємо при суміщенні площин проекцій. На рисунку 1.3 показано епюр точки А і зображено приклад проектування точки, яка знаходиться в І чверті простору. При суміщенні площин проекцій, проекції точки А (А₁ і А₂) розміщені по обидві сторони від осі ОХ і на одному перпендикулярі до неї. Відстань від проекції А₂ до осі ОХ на епюрі відповідає відстані від точки А до горизонтальної площини проекцій, відстань від проекції А₁ до осі ОХ відповідає відстані від точки А до фронтальної площини проекцій. А₁А₂  лінія проекційного зв’язку.

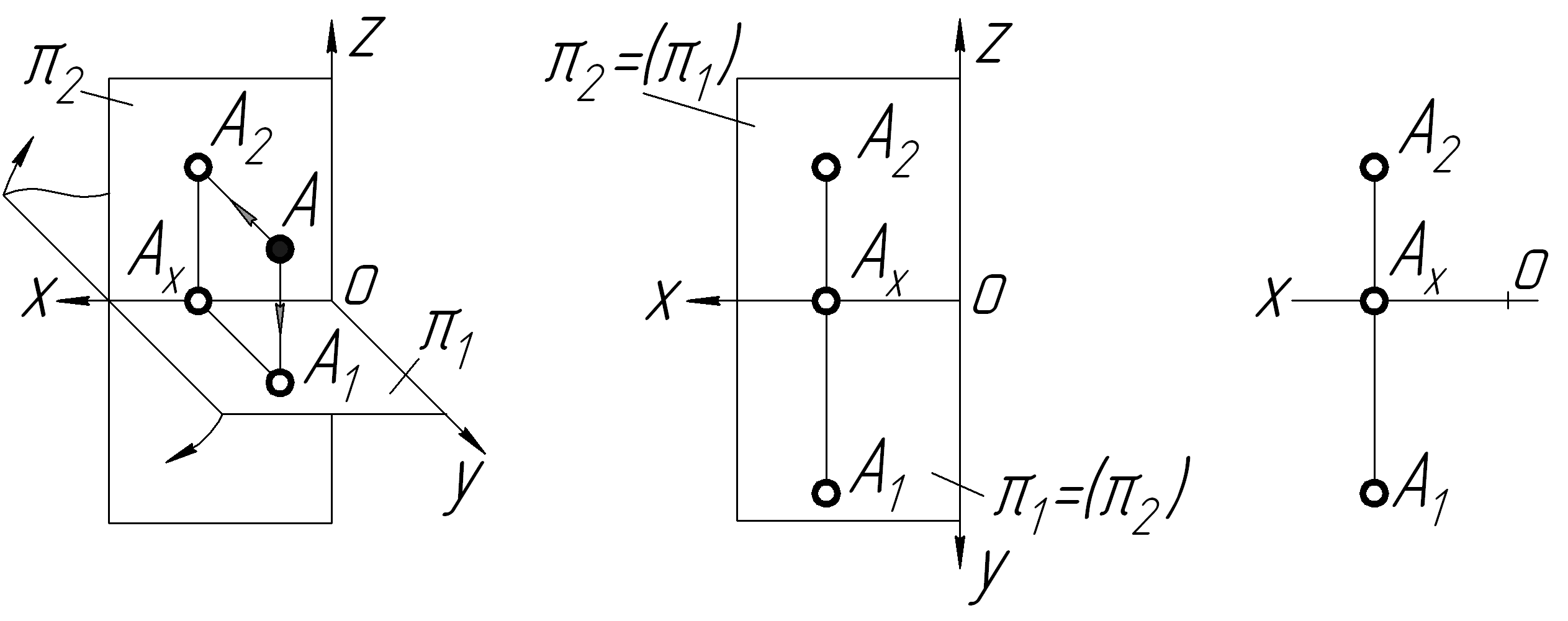
Рисунок 1.3 ─ Послідовність утворення епюру

В таблиці 1.2 зведені приклади епюрів точок, розміщених в І, ІІ, ІІІ, ІV чвертях простору.

Таблиця 1.2 – Точка в чвертях простору

Чверть	Наочне зображення	Епюр
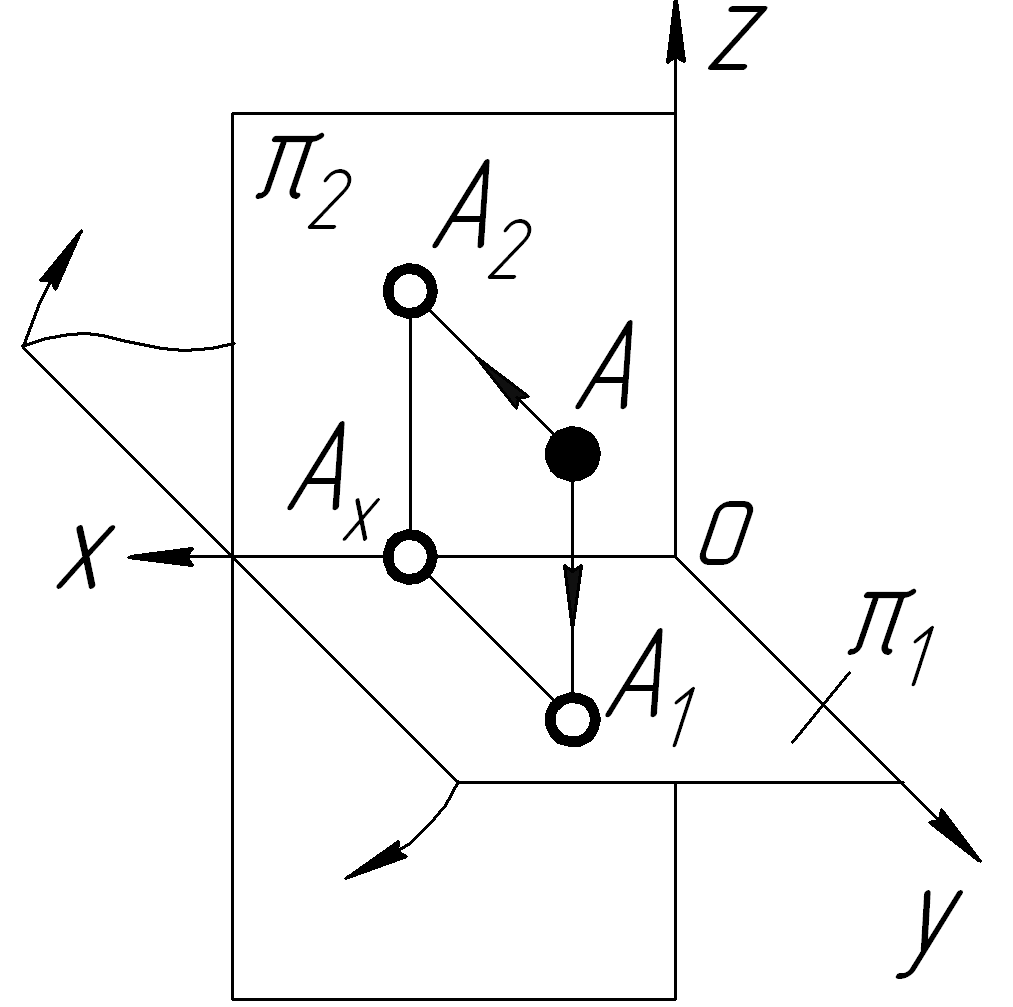
І
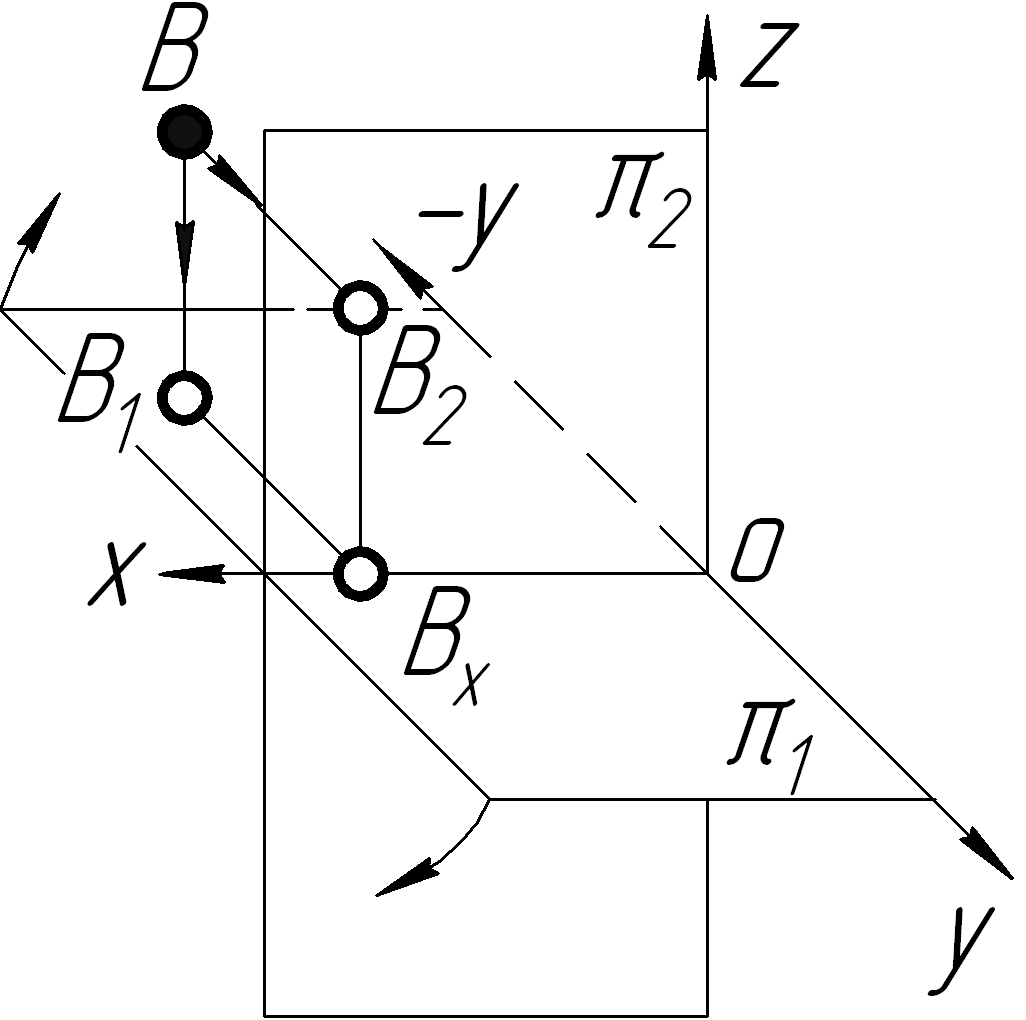
ІІ
Продовження таблиці 1.2
Чверть	Наочне зображення		Епюр
ІІІ
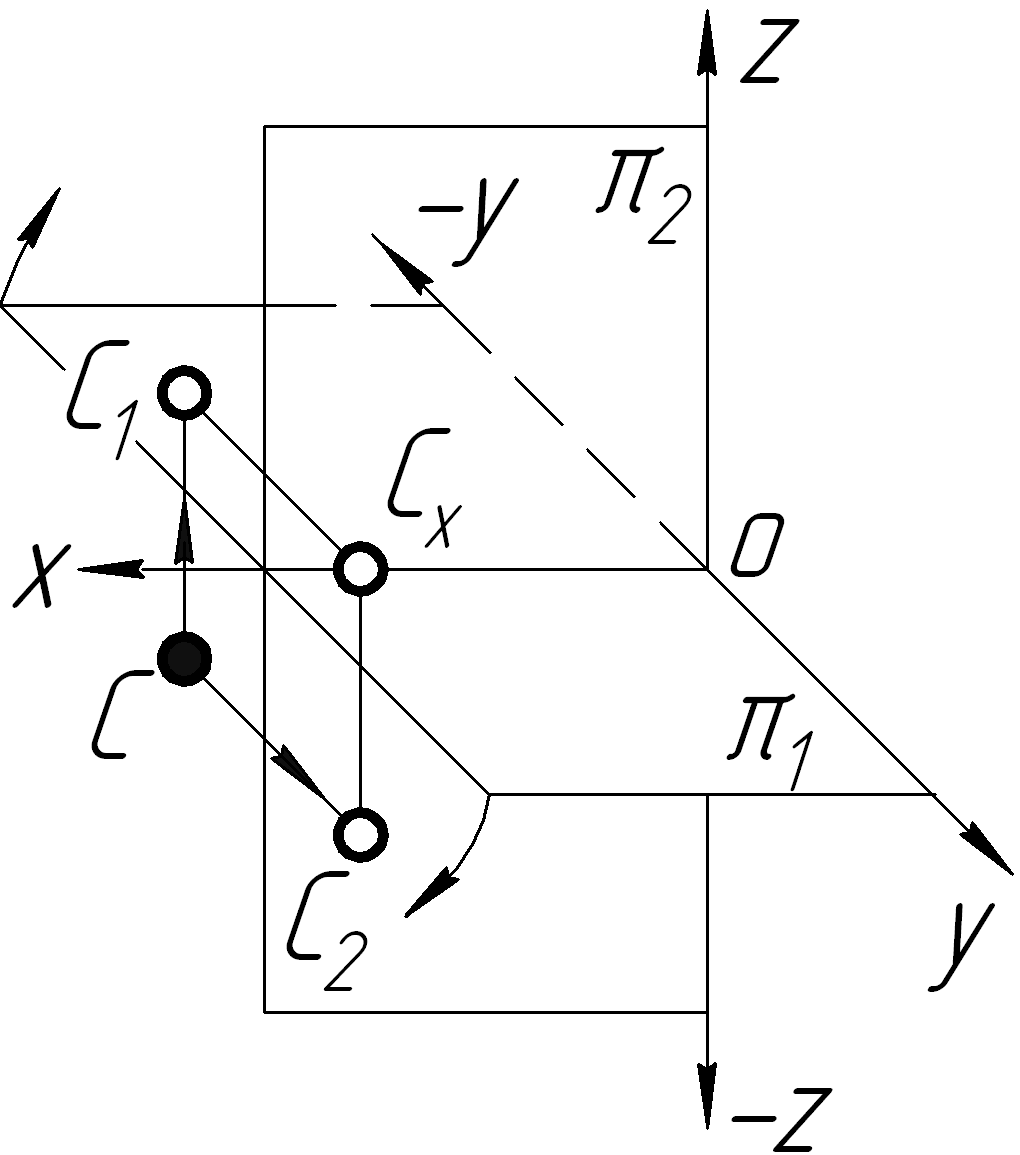
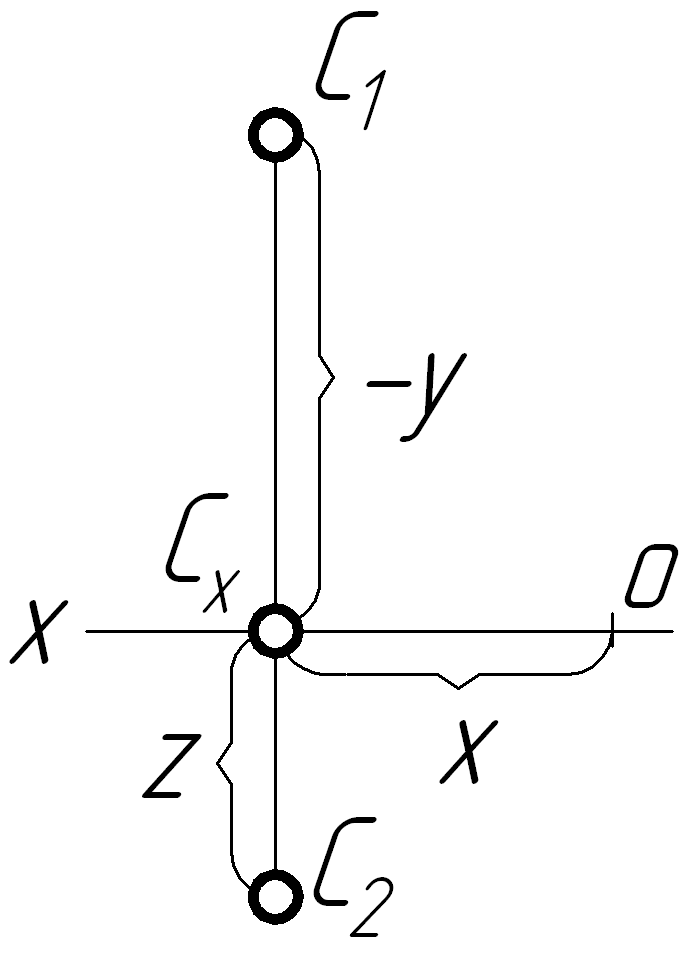
ІV

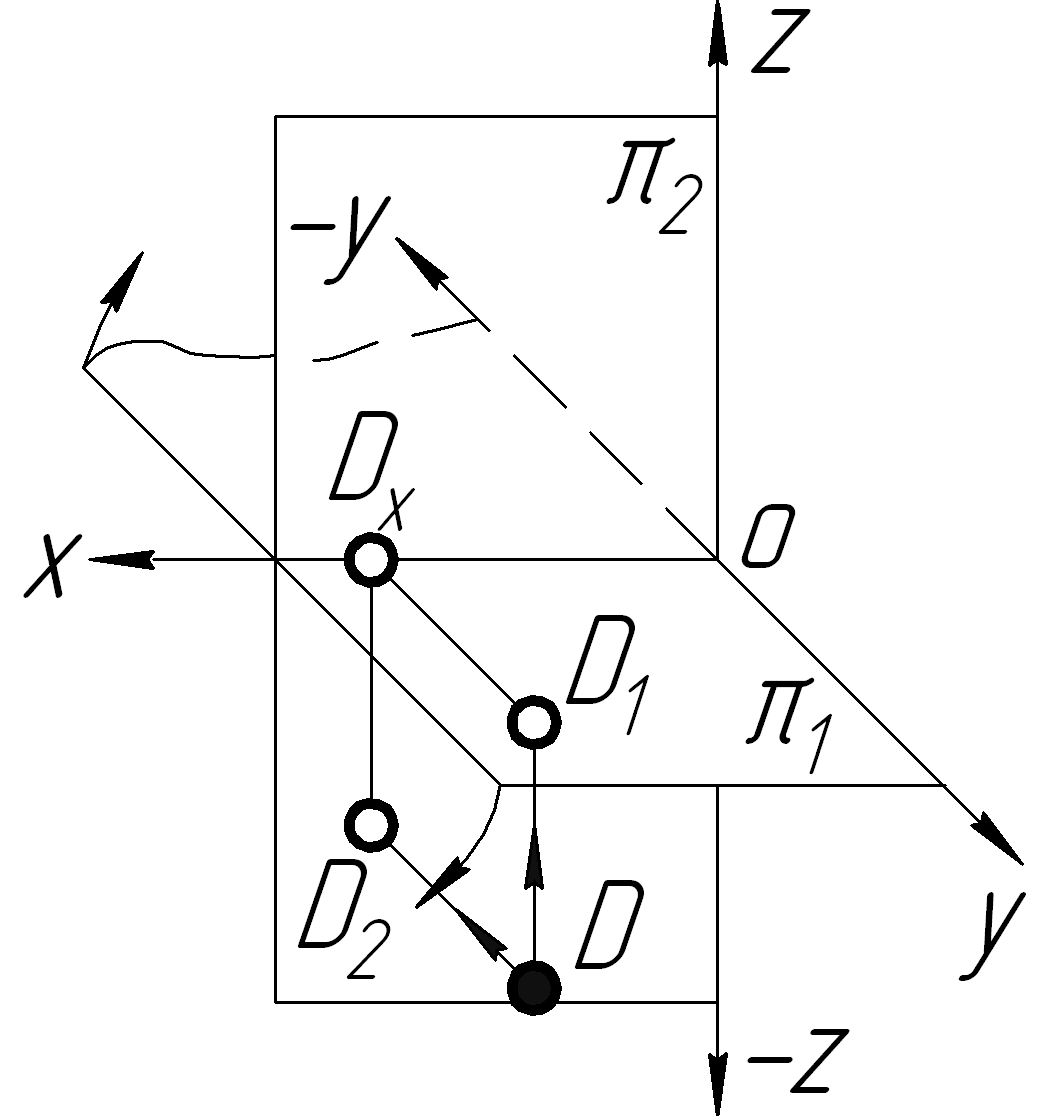
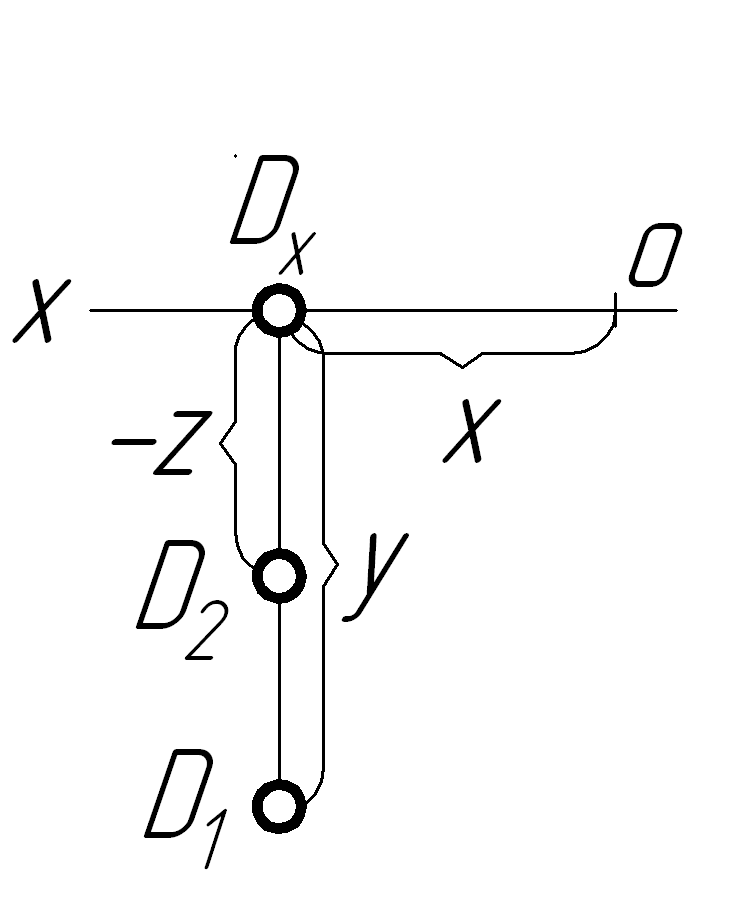
З таблиці 1.2 видно, що точка А знаходиться в просторі І чверті, точка В – в ІІ чверті, точка C– в ІІІ чверті і точка D – в ІV чверті

Якщо точка лежить на площинах проекцій, то одна її проекція обов’язково співпадає з даною точкою, а друга – лежить на осі проекцій. Одна із координат рівна нулю.

Таблиця 1.3 – Проекції точок, які лежать в площинах проекції

Необхідна умова	Наочне зображення		Епюр
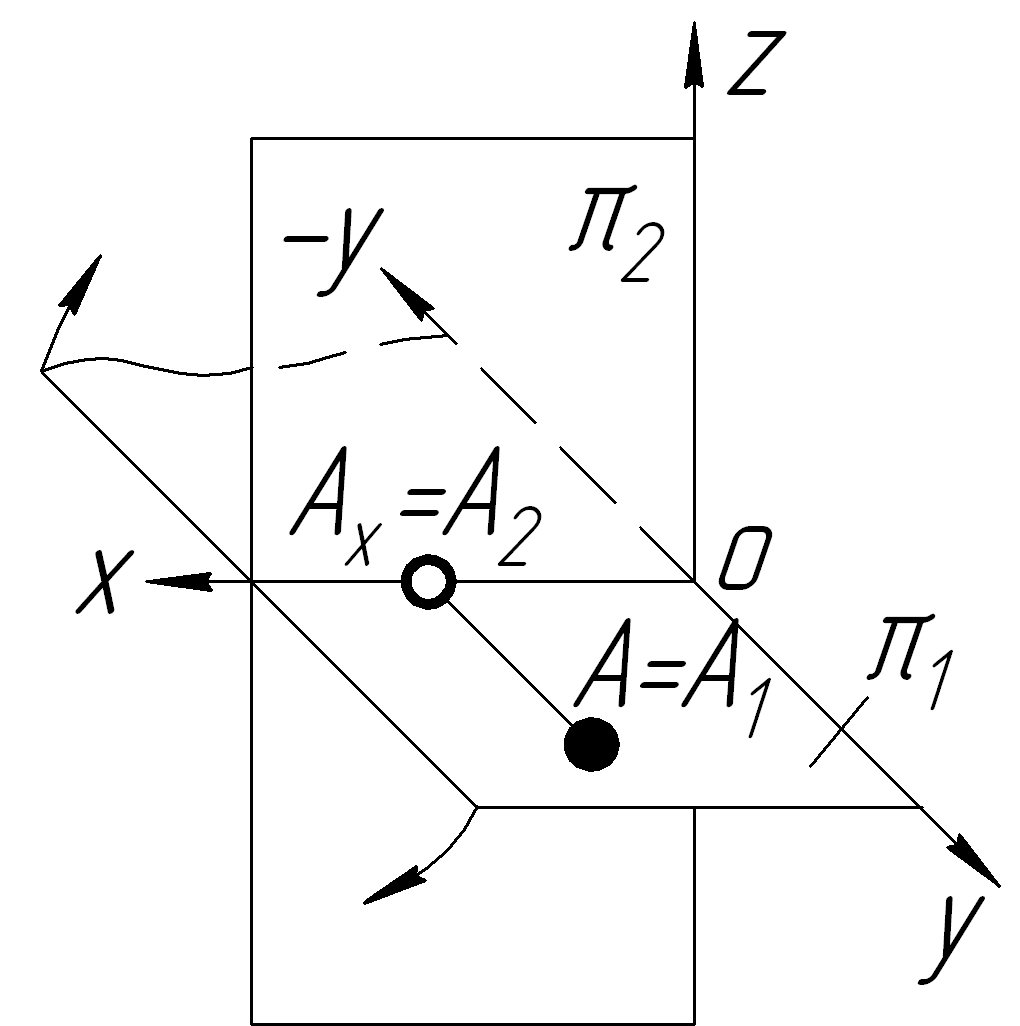
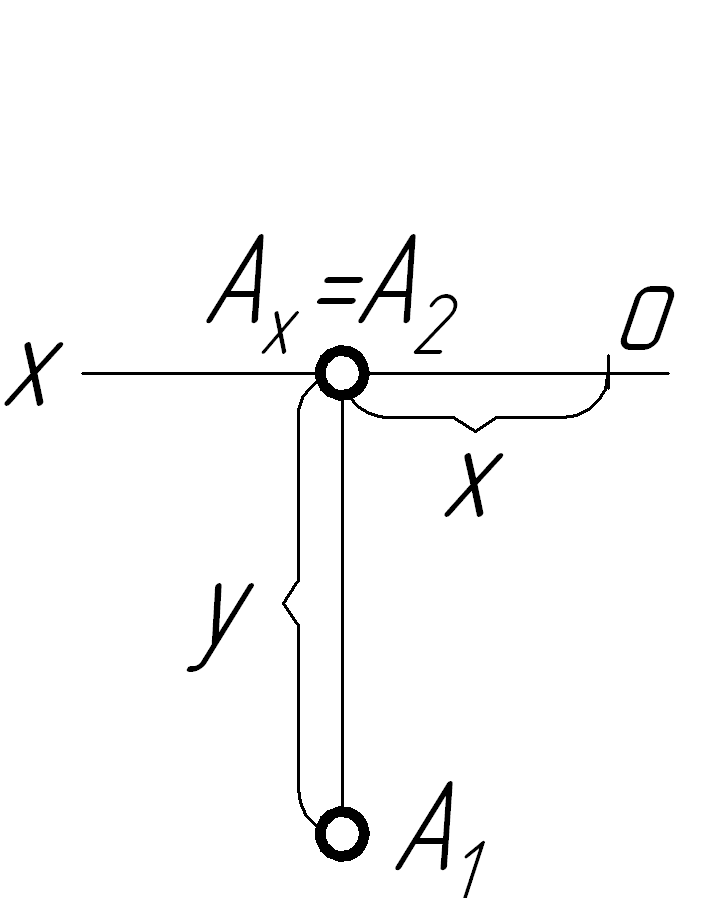
На передній полі 1 Z=0 Y0
Продовження таблиці 1.3
Необхідна умова	Наочне зображення	Епюр
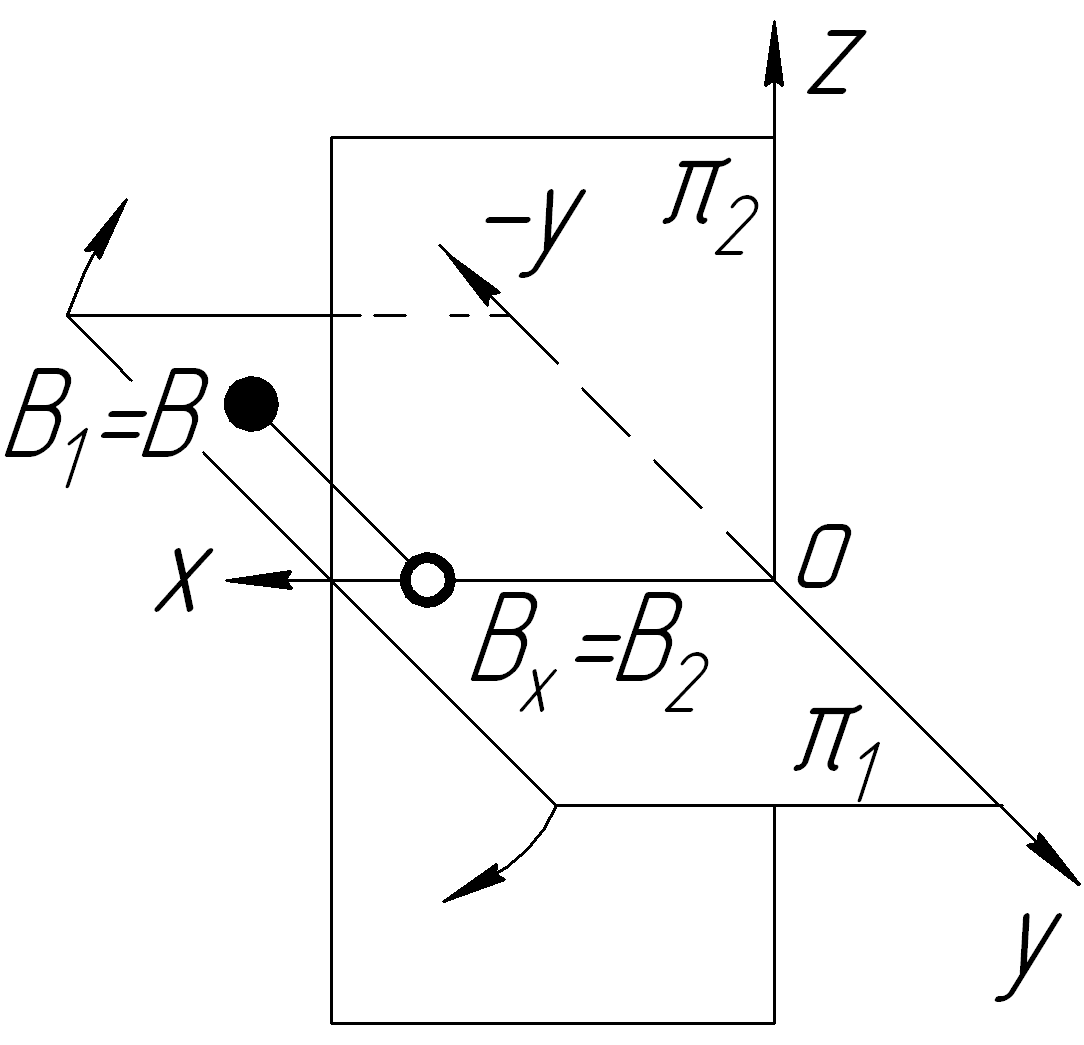
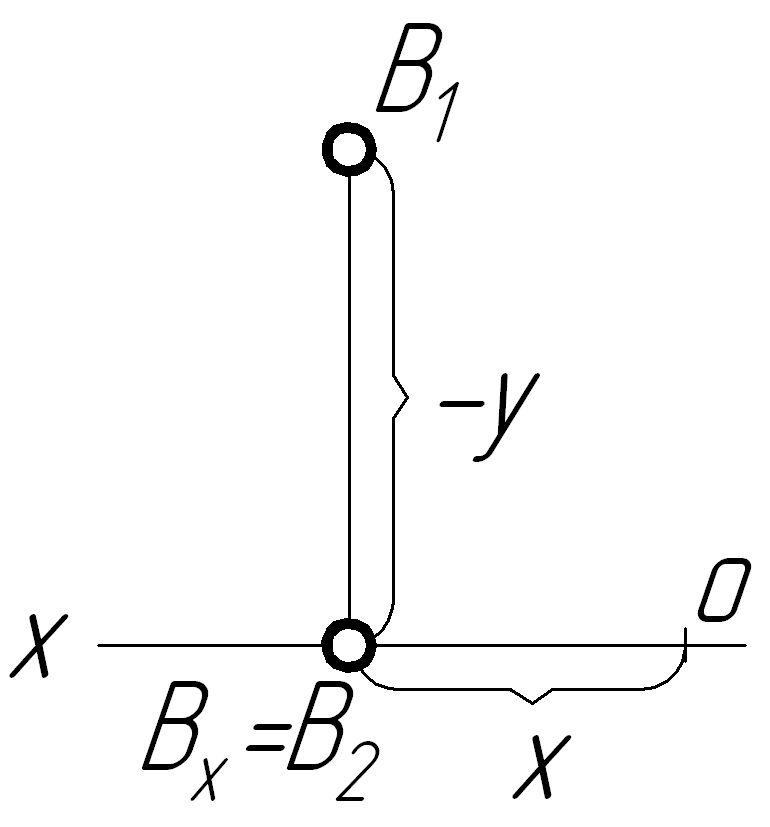
На задній полі p1 Z=0 Y0
На верхній полі p2 Y=0 Z>0
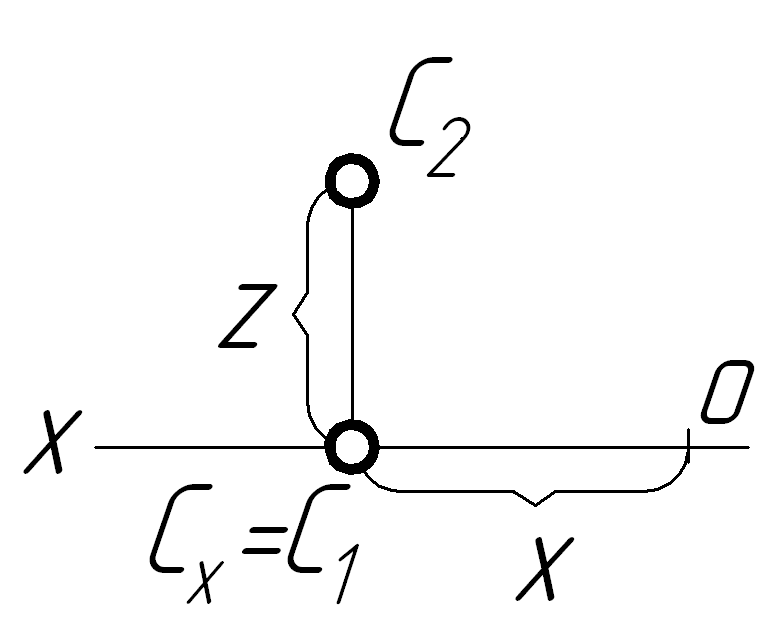
На нижній полі p2 Y=0 Z0
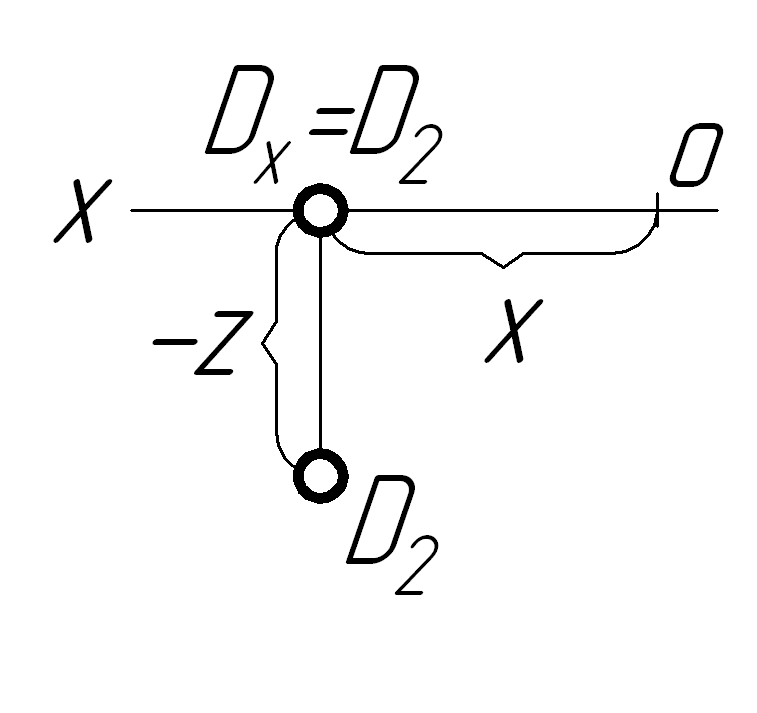
На осі OX Z=Y=0

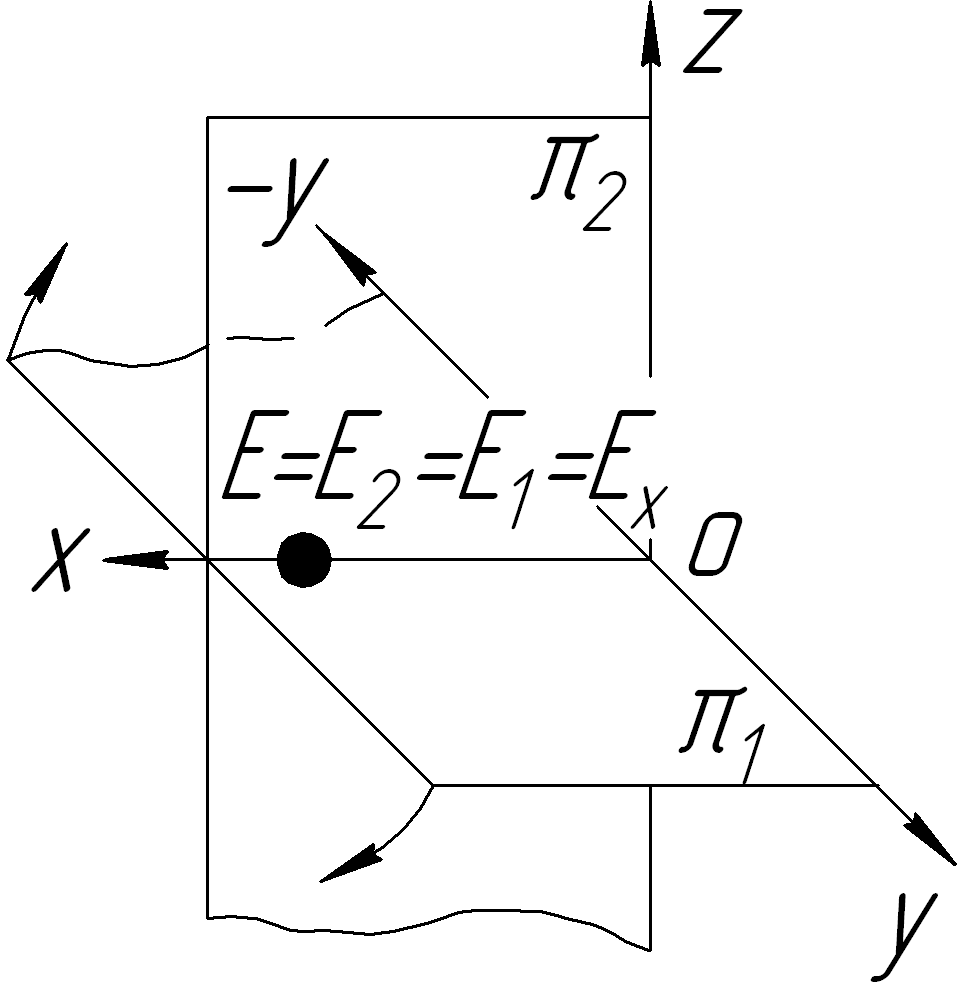
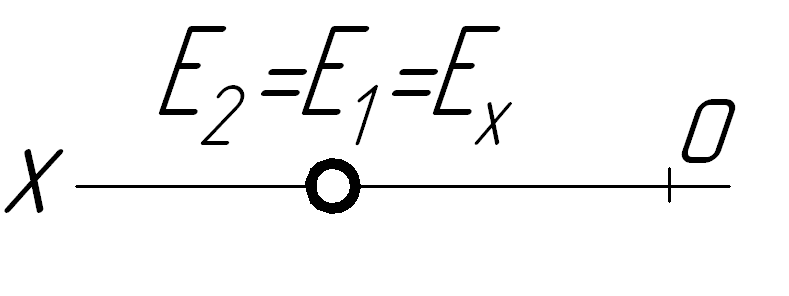
Наочні зображення і епюри точок, які лежать в площинах проекцій, показані в таблиці 1.3: точка А – в горизонтальній площині проекцій на її передній полі;

точка В – в горизонтальній площині проекцій на її задній полі;

точка С – у фронтальній площині проекцій на її верхній полі;

точка D – у фронтальній площині проекцій на її нижній полі;

точка Е – на осі проекцій (одночасно лежить на двох площинах проекцій, тому обидві проекції точки Е співпадають з даною точкою і дві координати рівні нулю.