Запитання та завдання для самоперевірки
Чим зумовлюється необхідність перетворення проекцій?
Назвіть способи перетворення проекцій та їх суть.
Які основні задачі можна розв’язати за допомогою перетворення проекцій?
Чому при заміні площин проекцій зберігається взаємна перпендикулярність площин проекцій нової і старої системи?
Яке положення повинна займати плоска фігура, щоб визначити її дійсну величину заміною однієї площини проекцій? Двох площин?
Задайтесь координатами вершин довільного трикутника АВС і точки D поза трикутником. Визначте відстань від точки D до площини трикутника.
Визначте відстаньодним із методів перетворення проекцій:
а) від точки до прямої довільного положення;
б) між двома паралельними прямими довільного положення;
в) між двома мимобіжними прямими.
Назвіть елементи обертання та їх призначення.
Яке положення може мати вісь обертання і як це позначається на складності розв’язку задач?
Які переваги і чому має спосіб плоско-паралельного переміщення?
Способом плоско-паралельного переміщення:
визначте відстань між двома паралельними прямими загального положення;
б) знайдіть центр кола, описаного навколо довільного трикутника.
Як розташовується площина обертання точки відносно осі обертання?
а) паралельно осі обертання;
б) перпендикулярно до осі обертання;
в) під довільним кутом до осі обертання.
У якій площині обертається точка, якщо вона обертається навколо горизонтально-проекційної осі?
а) у горизонтальній площині
б) у фронтальній площині;
в) у горизонтально-проекційній площині;
г) у фронтально-проекційній площині.
У якій площині обертається точка, якщо вона обертається навколо фронтальної осі?
а) у горизонтальній площині;
б) у фронтальній площині;
в) у горизонтально-проекційній площині;
г) у фронтально-проекційній площині.
На якому епюрі правильно розпочато переведення горизонтального відрізка АВ1(А1В1,1А2В2) у проекційне положення способом плоскопаралельного переміщення?
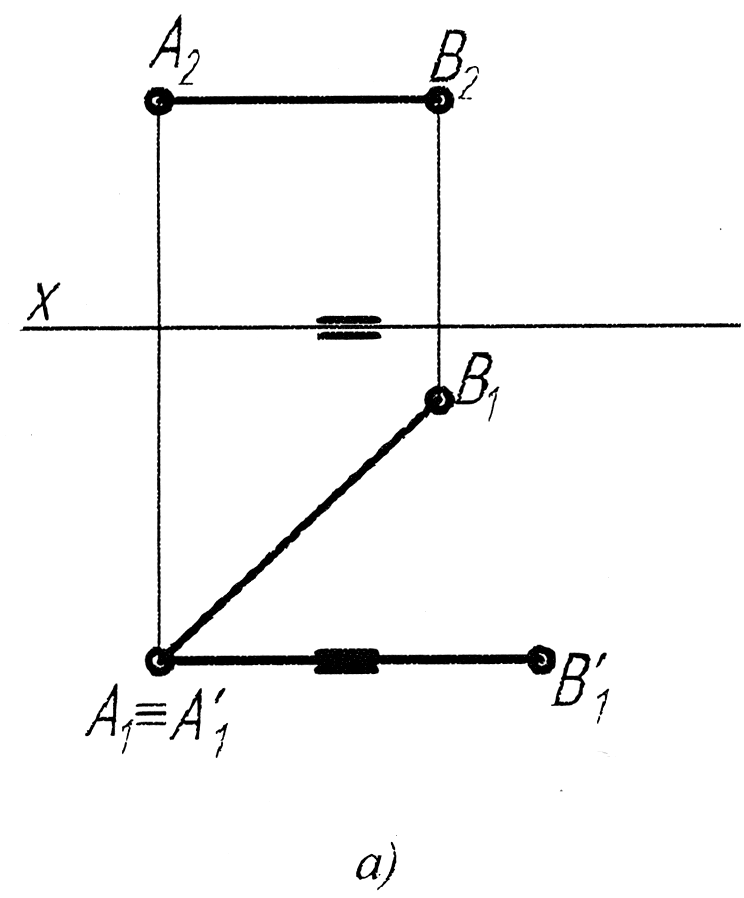
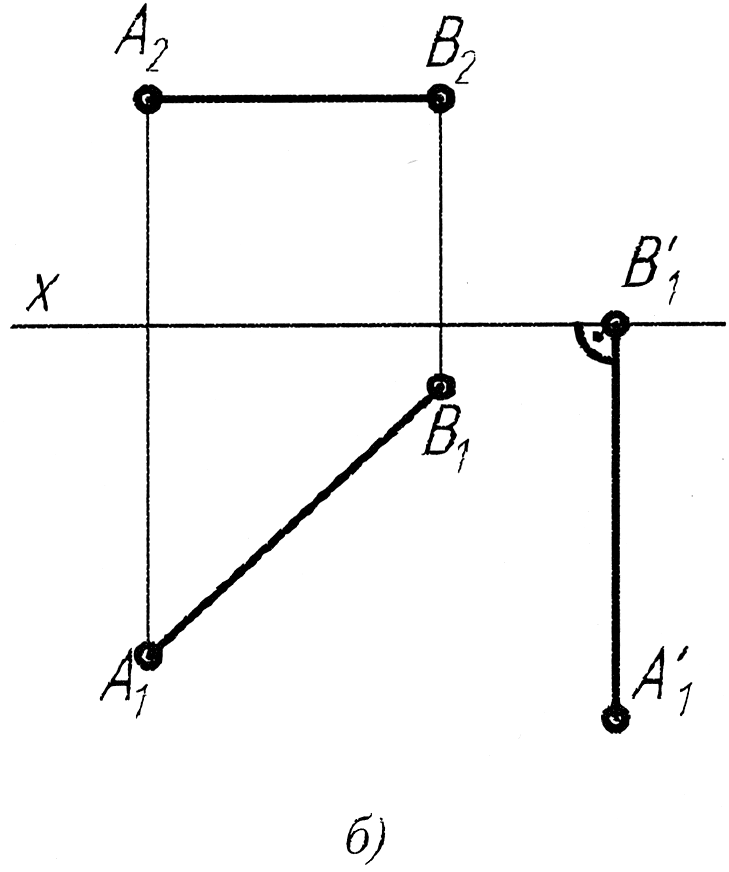
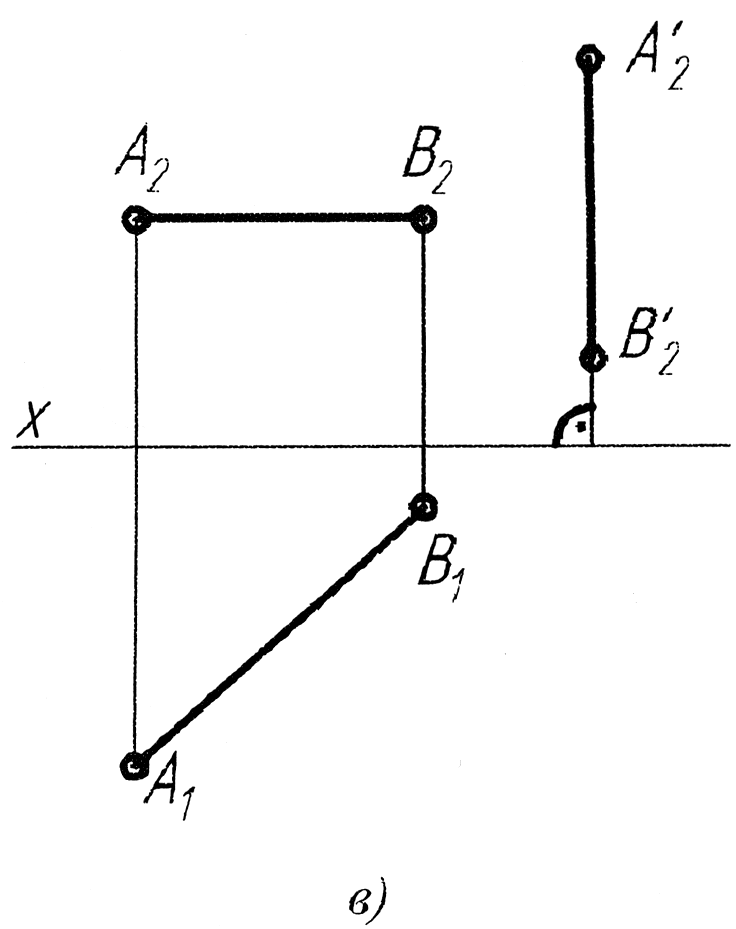
Який відрізок і як його треба розташувати при плоско- паралельному переміщенні, щоб трикутник ABC перевести у фронтально-проекційне положення?
-
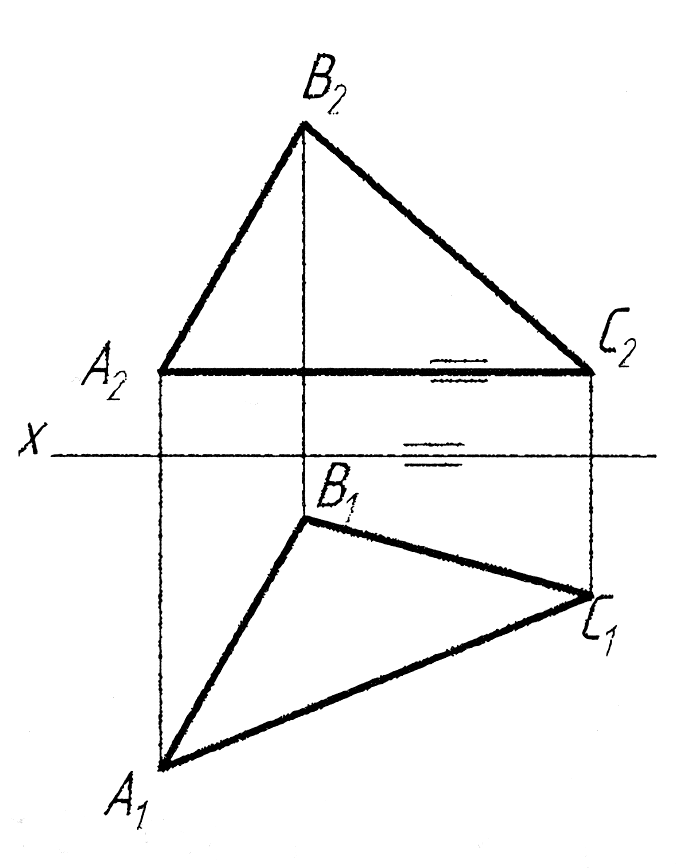
а) А1В1 перпендикулярно до осі проекцій;
б) А1C1 перпендикулярно до осі проекцій;
в) А1С1 паралельно осі проекцій;
г) В1С1 перпендикулярно до осі проекцій.
На якому епюрі правильно розпочато переведення площини, заданої трикутником abc (a1b1c1, а2в2с2), у проекційне положення способом плоскопаралельного переміщення?
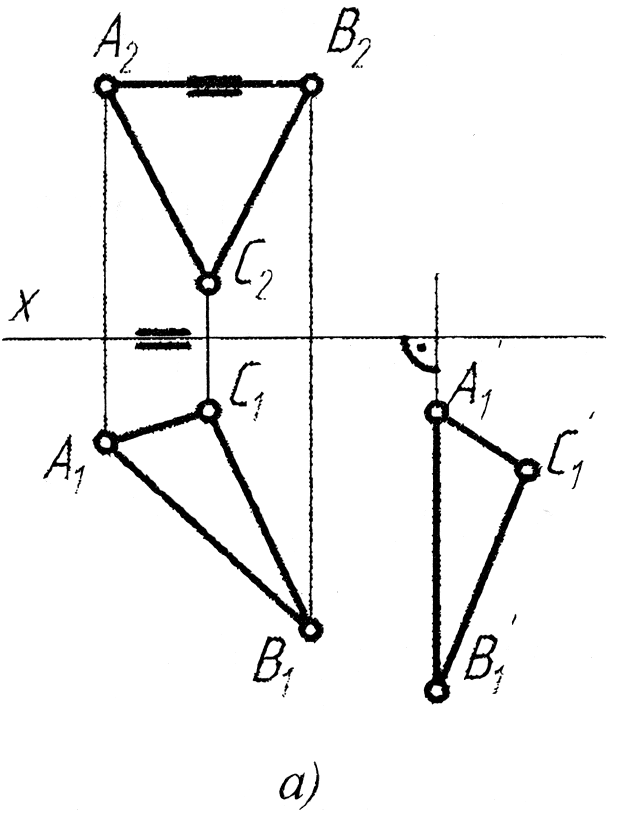
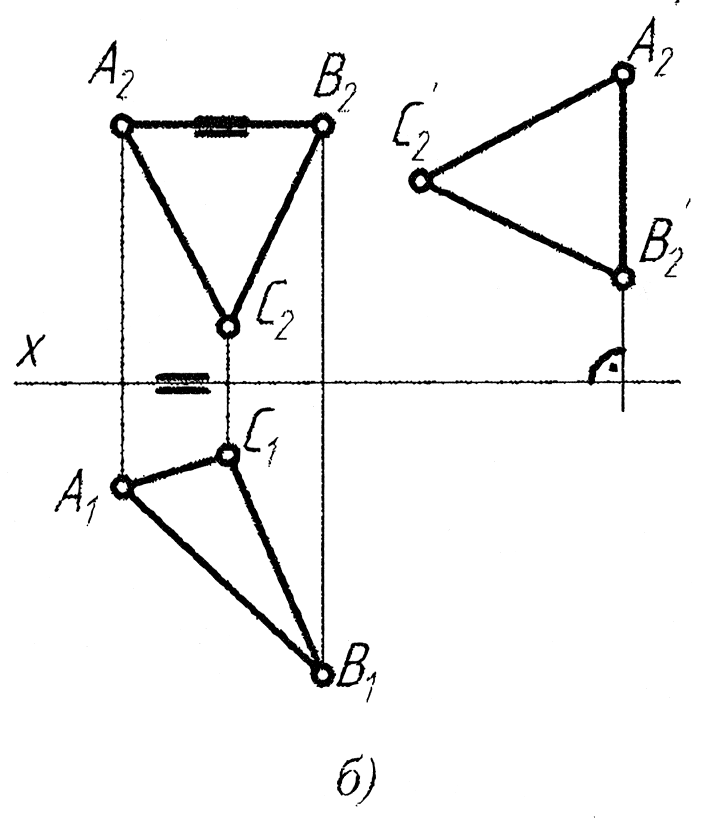
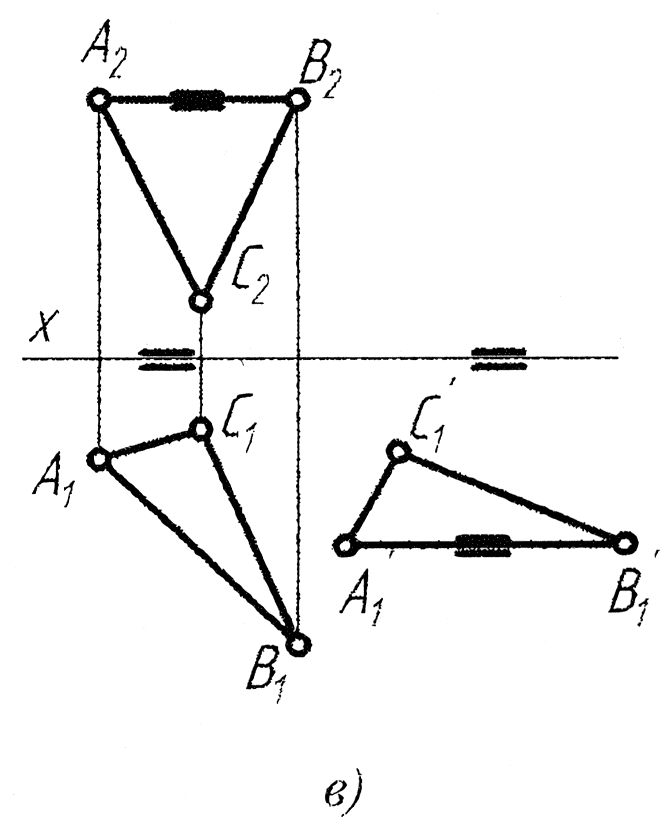
Як розташовується суміщена горизонталь площини при суміщенні останньої з горизонтальною площиною проекцій?
а) паралельно суміщеному фронтальному слідові площини;
б) паралельно горизонтальному слідові площини;
в) паралельно осі проекцій.
Як розташовується суміщена фронталь площини при суміщенні останньої з фронтальною площиною проекцій?
а) паралельно суміщеному горизонтальному слідові площини;
б) паралельно фронтальному слідові площини;
в) паралельно осі проекцій.