2.3.3 Плоско-паралельне переміщення

Плоско-паралельне переміщення є способом обертання навколо осей – проекційних прямих, які не визначені на епюрі. Здійснюючи плоско-паралельне переміщення геометричної фігури відносно площин проекцій, виходимо з того, що всі точки фігури, змінюючи своє положення у просторі, переміщаються в площинах, паралельних між собою і паралельних до однієї з площин проекцій.

Задача 3 Знайти дійсну величину трикутника АВС методом плоско-паралельного переміщення (рис.2.50).

Трикутник АВС в умові задачі є горизонтально-проекцйною площиною. Для того, щоб знайти його дійсну величину, необхідно поставити трикутник у положення, паралельне площині проекцій ₂. Для цього виконаємо плоско-паралельне переміщення трикутника АВС вправо на вільне місце, тобто повертаємо навколо деякої уявної осі, перпендикулярної до площини П₁. Перенесемо горизонтальну проекцію трикутника АВС на нове місце, вигідне для побудови, не змінюючи величини і форми проекції, у даному випадку – прямої А₁С₁. Нове зображення А′₁В′₁С′₁ трикутника розміщуємо в положення, паралельне до осі ОХ, тобто площина трикутника стає фронтальною площиною. Побудована нова фронтальна проекція трикутника і буде його дійсною величиною. При переміщенні вершини трикутника переміщаються в уявних площинах обертання Σ, Δ, α паралельних між собою і паралельних площині ₁. Таким чином, висоти точок А, В, С (координати Z_А, Z_В, Z_С) при переміщенні їх у нове положення залишаються незмінними.

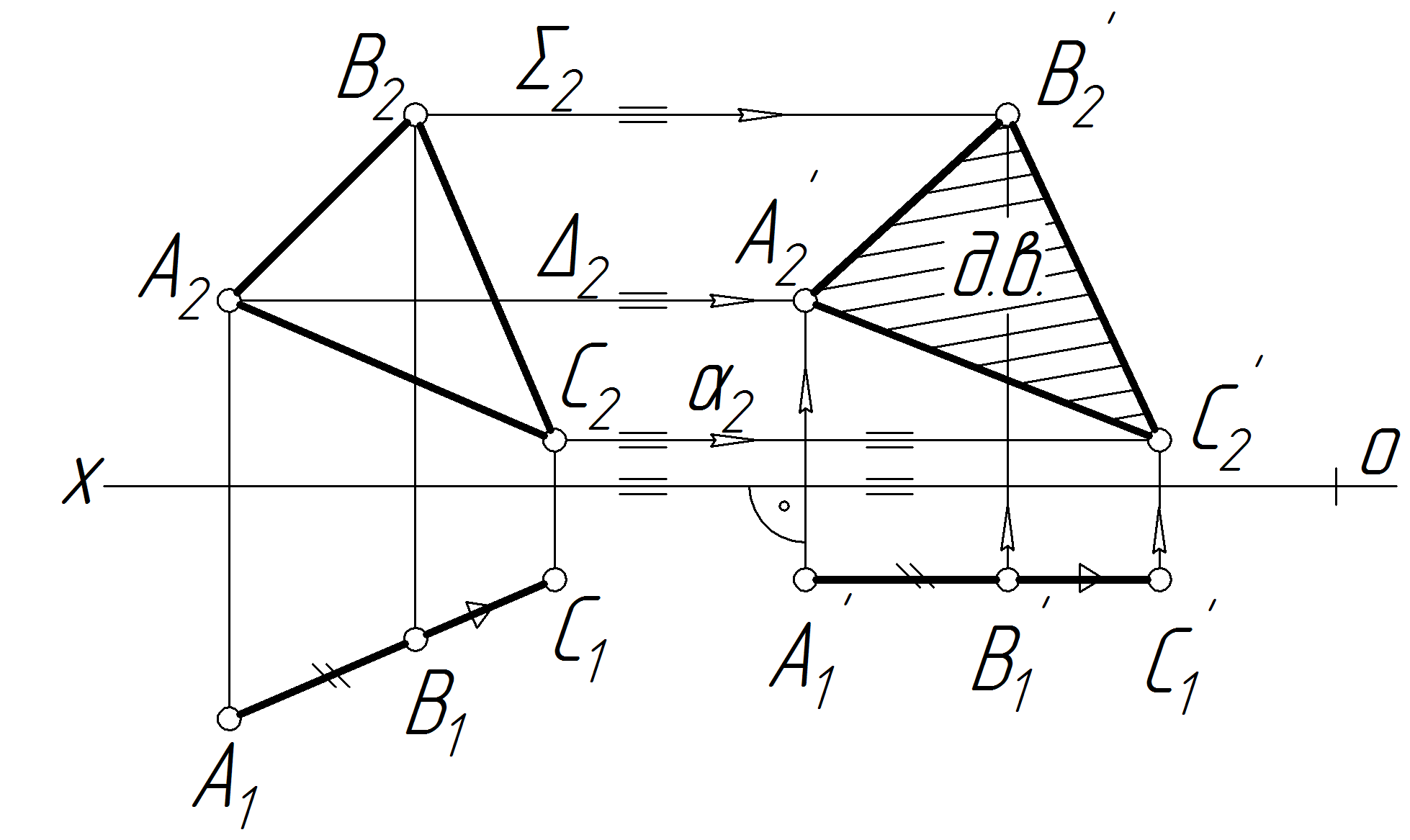
Рисунок 2.50

Задача 34 Відрізку АВ надати положення горизонтально-проекційної прямої (рис.2.51).

У даному випадку розв’язок задачі буде здійснюватися двома переміщеннями. Спочатку розташуємо відрізок у положення, паралельне до площини ₂, виконавши горизонтальне переміщення. Для цього горизонтальну проекцію А₁В₁ відрізка розміщуємо в новому місці А′₁В′₁ паралельно осі ОХ, не змінюючи величини проекції. Нова фронтальна проекція А′₂В′₂ – дійсна величина відрізка АВ. Фронтальним переміщенням переносимо фронтальну проекцію А′₂В′₂ у нове положення А′′₂В′′₂ перпендикулярно до осі ОХ, зберігаючи величину проекції. Тоді нова горизонтальна проекція перетвориться в точку А′′₁ =В′′₁. Отже, відрізок АВ після другого переміщення стане перпендикулярним до ₁.

Рисунок 2.51

У способі заміни площин проекцій наявність осуй проекцій — обов’язкова, тому що від них здійснюється відлік відстаней, а у способі плоско-паралельного переміщення осі можна не фіксувати, бо вони не впливають на одержані результати.

Задача 35 Знайти дійсну величину трикутника АВС (рис.2.52)

У даному випадку трикутник АВС є площиною довільного положення. Поставимо його у проекційне положення. За допомогою проведеної горизонталі С₁ повернемо його навколо вертикальної невиявленої осі так, щоб горизонталі розташувалися перпендикулярно до площини проекцій ₂. При такому положенні горизонталь спроектується у точку, а весь трикутник — у лінію А₂'В₂'С₂' . Нарешті, розташуємо лінійну проекцію А₂'В₂'С₂' паралельно площині проекцій ₁, при цьому відбуваєтьбся обертання трикутника АВС навколо фронтально-проектуючої невидимої осі. Трикутник А₁''В₁''С₁'' є дійсною величиною трикутника АВС.

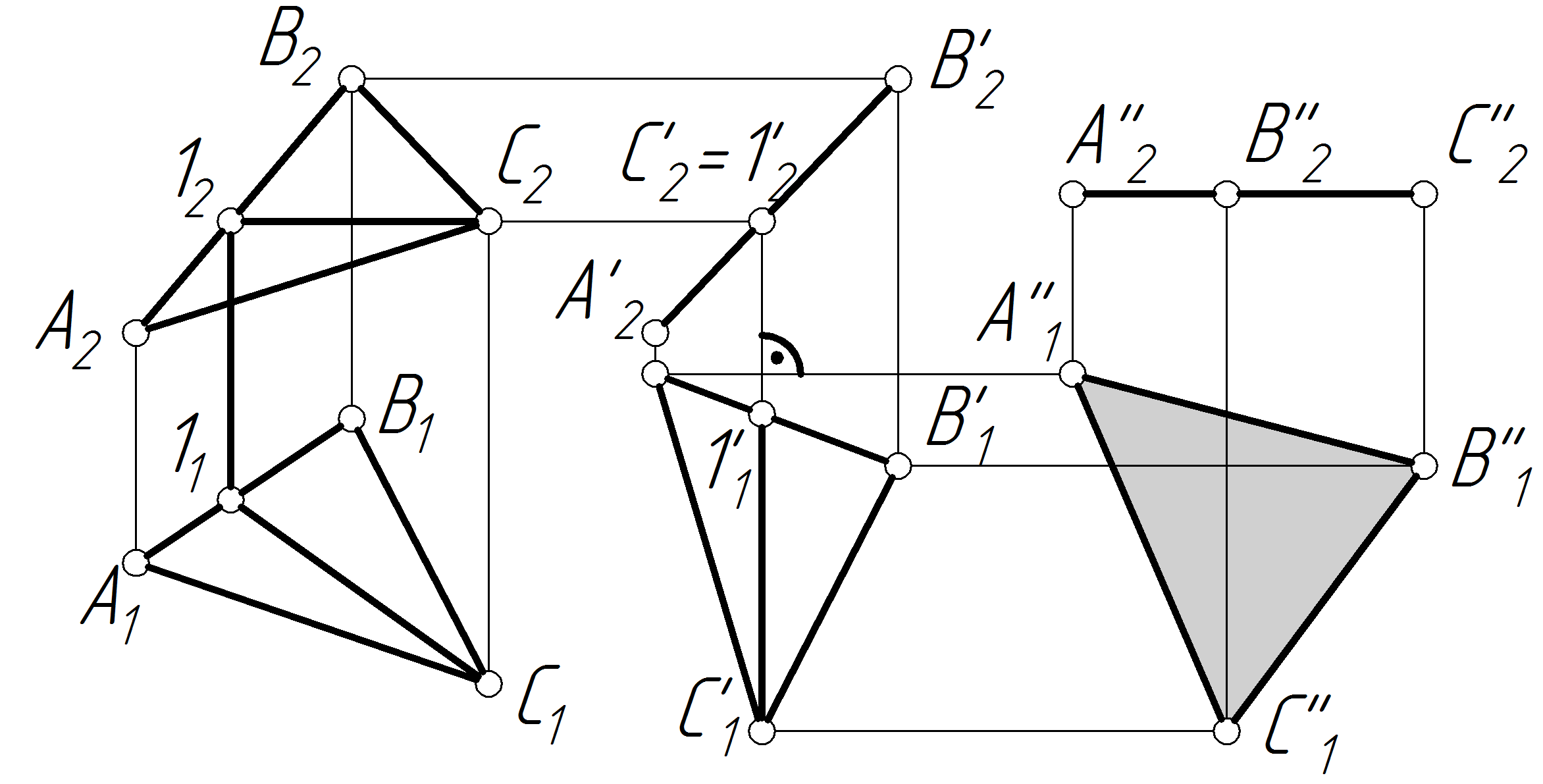
Рисунок 2.52

Задача 36 Способом полоскопаралельного переміщення знайти дісну величину двогранного кута між двома трикутниками зі спільним ребром АВ (рис.2.53)

П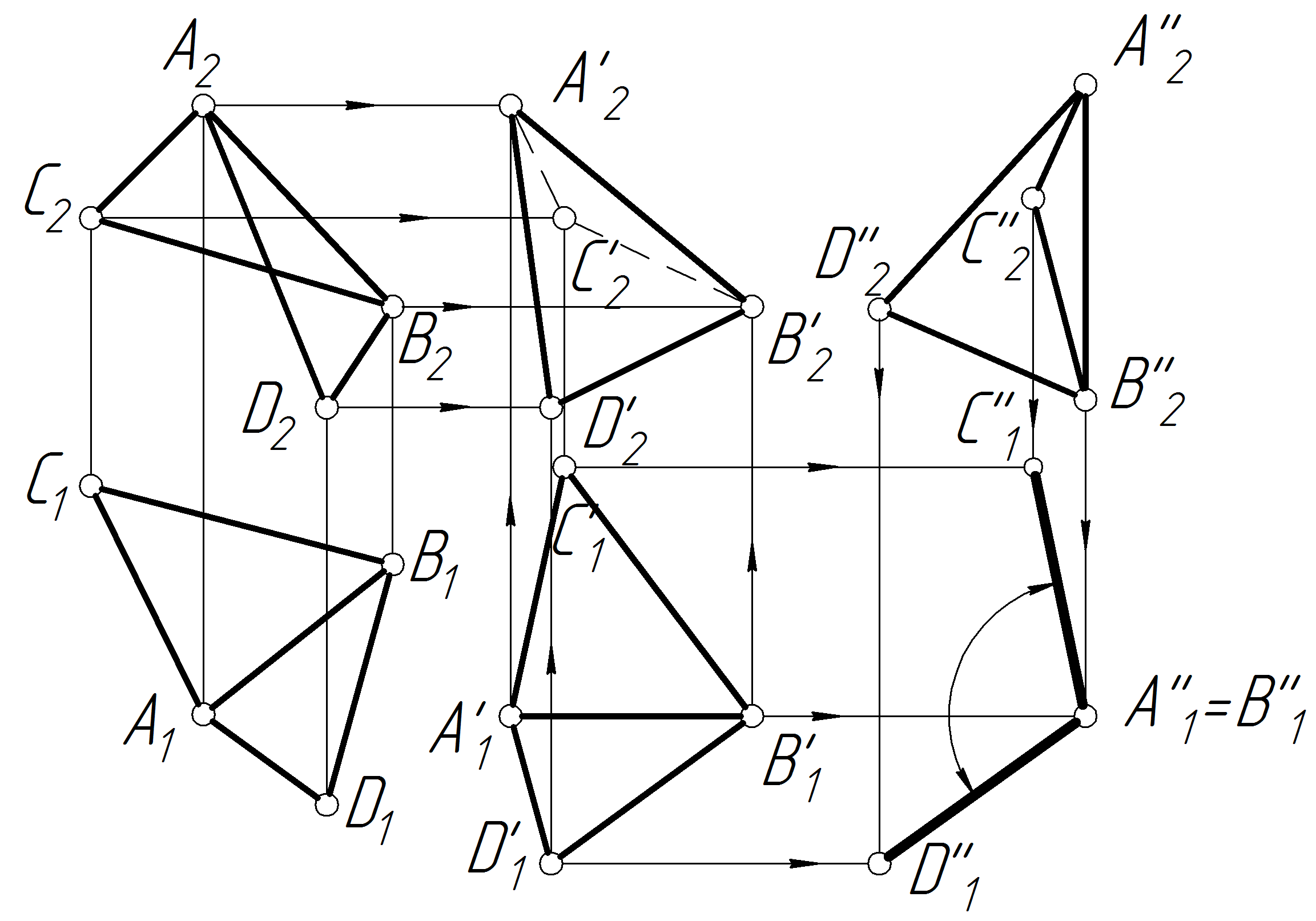 ершим кроком буде поворот навколо вертикальної невиявленої осі двогранного кута так, щоб ребро АВ було паралельним фронтальній площині проекцій ₂ і спроектувалося у дійсну величину. Другим кроком буде поворот навколо невиявленої фронтально-проекційної осі. Двогранний кут розташується таким чином, щоб його спільне ребро стало вертикальним, тоді воно спроектується на ₁ у точку. Двогранний кут при цьому спроектується у дійсну величину.

Рисунок 2.53