2.3.Способи перетворення проекцій

Метричні та позиційні характеристики геометричних образів легко визначити при їх окремому положенні відносно площин проекцій. Оскільки на практиці геометричні образи найчастіше знаходяться у загальному положенні, треба їх привести з цього загального положення в особливе. У результаті цього нові проекції дозволять просто й зручно виявити форму елементів, взаємне положення та дійсні величини прямих, фігур, кутів тощо.

Метричні задачі зводяться до розв’язання чотирьох основних задач:

1) перетворення прямої загального положення у пряму рівня;

2) перетворення прямої загального положення у проекційну;

3) перетворення площин загального положення у проекційну;

4) перетворення площин загального положення у площину рівня.

2.3.1 Заміна площин проекцій

Суть цього способу полягає в тому, що початкову систему площин проекцій ₂, ₁, у якій заданий геометричний образ займає загальне положення, заміняють іншою, новою системою площин проекцій так, щоб геометричний образ зайняв певне положення, що спростить розв’язування задачі. Положення самого образу в просторі залишається при цьому незмінним (рис.2.32, 2.33). Нові додаткові площини проекцій вводять так, щоб задані геометричні елементи зображалися на них у вигідному для конкретної задачі положенні. Цим зумовлюється заміна однієї або двох площин проекцій. Якщо замінити тільки одну площину проекцій, то зрозуміло, що система двох площин проекцій буде складатися з однієї площини проекцій початкової системи ₂, ₁ і однієї нової, додаткової площини проекцій ₄ або ₅ (рис. 2.32, 2.33).

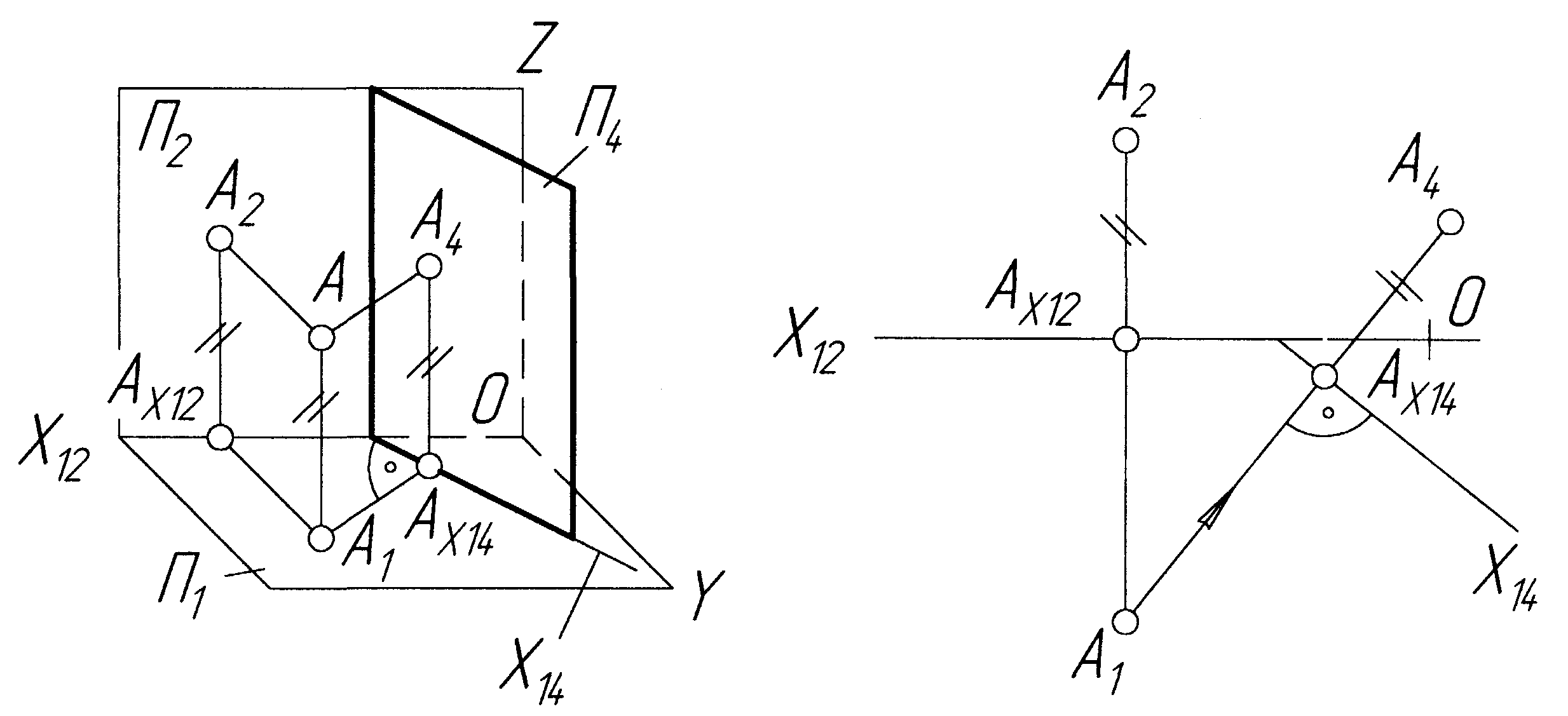
Рисунок 2.32 — Заміна фронтальної площини проекцій ₂ на ₄ (₄₁)

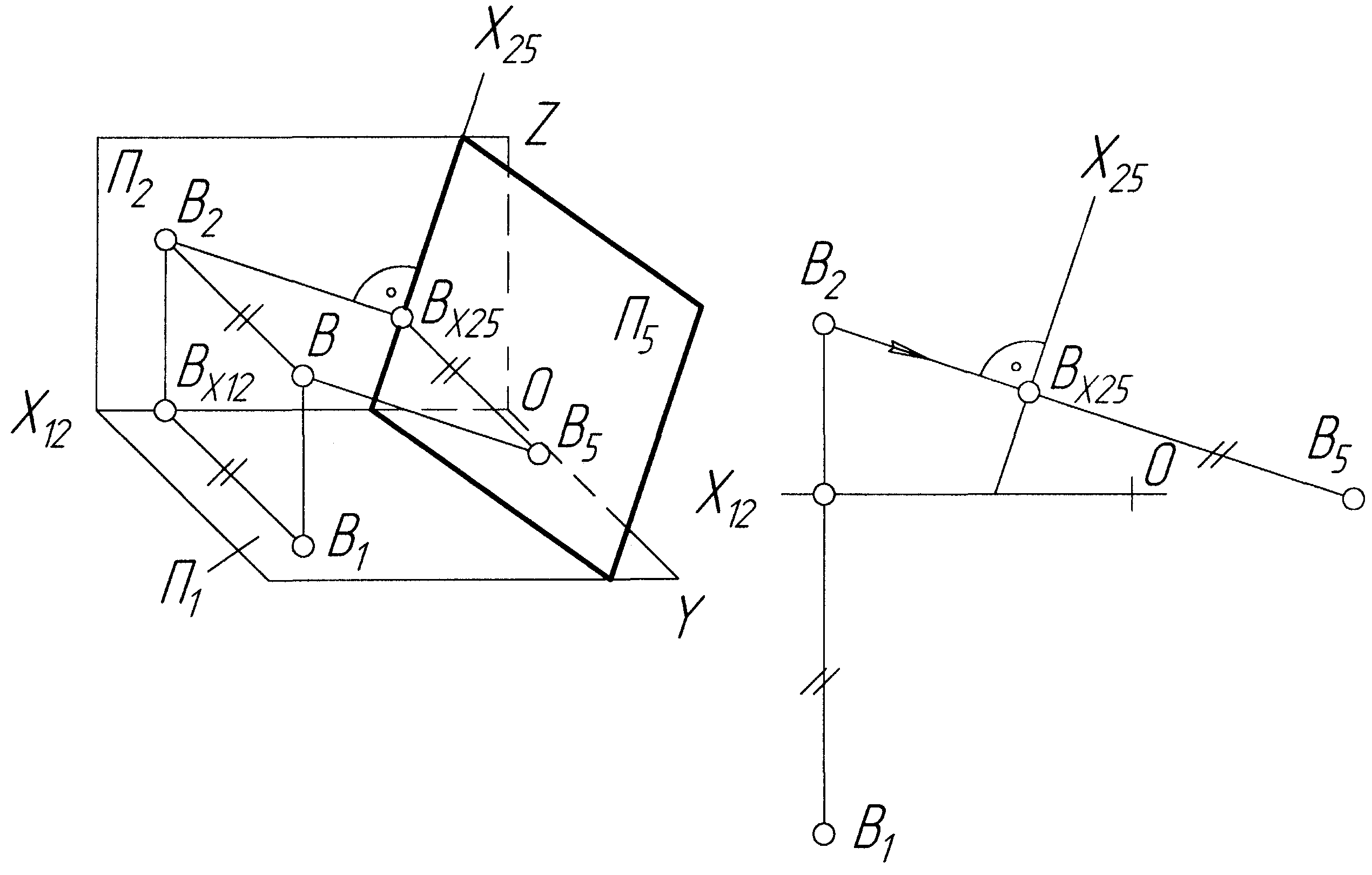
Рисунок 2.33 — Заміна горизонтальної площини проекцій ₁ на ₅ (₅₂)

Нехай у початковій системі площин проекцій ₂ - ₁ задана геометрична фігура у вигляді точки А (рис.2.32). Припустимо, що для розв’язування цієї задачі достатньо провести заміну однієї площини проекцій, наприклад, ₂ на ₄, перпендикулярну до ₁. Тоді в системі площин проекцій ₄ - ₁ з новою віссю Х₁₄, по якій площина ₄ перетинає ₁, проводимо перпендикуляр через точку А₁ до площини ₄ і знайдемо нову проекцію А₄, зазначимо, що відстань А₂Ах₁₂=АА₁=А₄Ах₁₄=Z_A. При розв’язуванні деяких метричних чи позиційних задач виникає потреба у послідовній заміні обох площин проекцій і утворенні таким чином нових систем площин проекцій ₄ – ₅.

З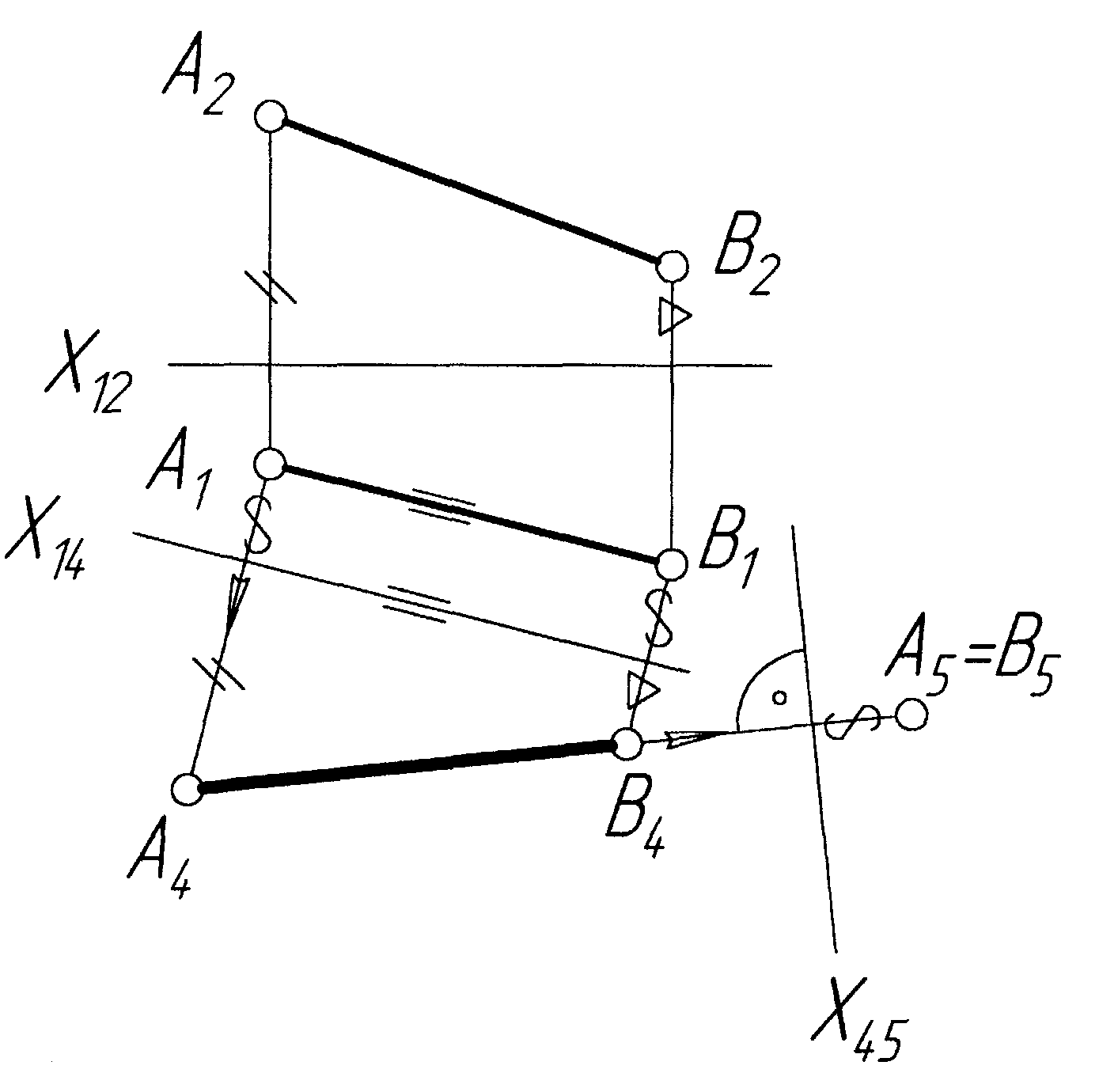 адача 19 Побудувати нові проекції відрізка АВ так, щоб він став проекційним (рис.2.34).

В

Рисунок 2.34

ідрізок стане проекційним тоді, коли він спроектується у точку. Цього можна досягти заміною двох площин проекцій, оскільки в початковій системі відрізок займає довільне положення. Після першої заміни ₂ на ₄, надаємо відрізку положення, паралельне до фронтальної площини проекцій. Нову площину проекцій ₄ проводимо так, щоб ₄  ₁ і нова вісь Х₁₄ була розміщена паралельно до А₁В₁. Після цього будуємо А₄В₄ ─ проводимо перпендикуляри з А₁ на Х₁₄, і з В₁ на Х₁₄. Відкладаємо на них Z_A і Z_B. Побудову показано стрілками і умовними позначками. А₄В₄ – дійсна величина відрізка1АВ.

Далі проводимо другу заміну площин проекцій, вводячи площину ₅ – замість ₁. При цьому нова вісь Х₄₅ має бути перпендикулярною до А₄В₄. Тоді нова проекція відрізка у системі ₄ – ₅ буде точкою А₅=В₅, тобто відрізок АВ стане перпендикулярним до площини проекцій ₅ (побудова показана стрілками і умовними позначками).

Задача 20 Знайти дійсну величину відстані від точки С до прямої, яка задана відрізком АВ.

О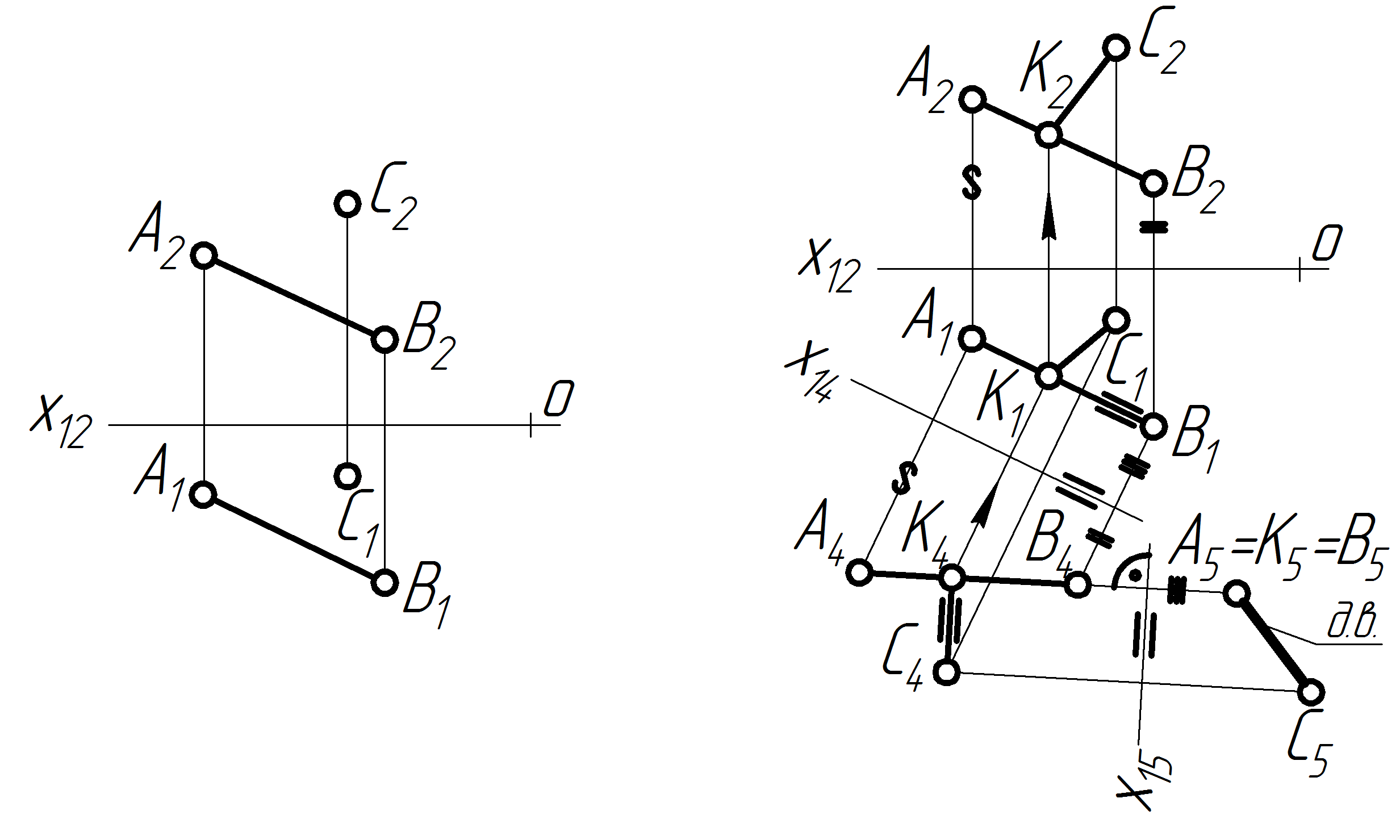 пустити перпендикуляр з точки на пряму безпосередньо на епюрі можна тільки у тому випадку, якщо пряма паралельна будь-якій з площин проекцій (на основі теореми про проектування прямого плоского кута). Отже, замінимо фронтальну площину проекцій ₂ новою ₄ , яка паралельна прямій АВ. Будуємо вісь проекцій Х₁₄ паралельно А₁В₁ і знайдемо нові проекції прямої А₄В₄ (дійсна величина АВ) і С₄ . опустимо з точки С₄ перпендикуляр на пряму А₄В₄ , знайдемо основу перпендикуляра К₄ . ще однією заміною ₁ на ₅ знайдемо дійсну величину відстані від точки С до відрізка АВ (побудова показана стрілками та умовними позначеннями).

Рисунок 2.35

Задача 21 Знайти відстань між двома мимобіжними, які задані відрізками АВ і СD.

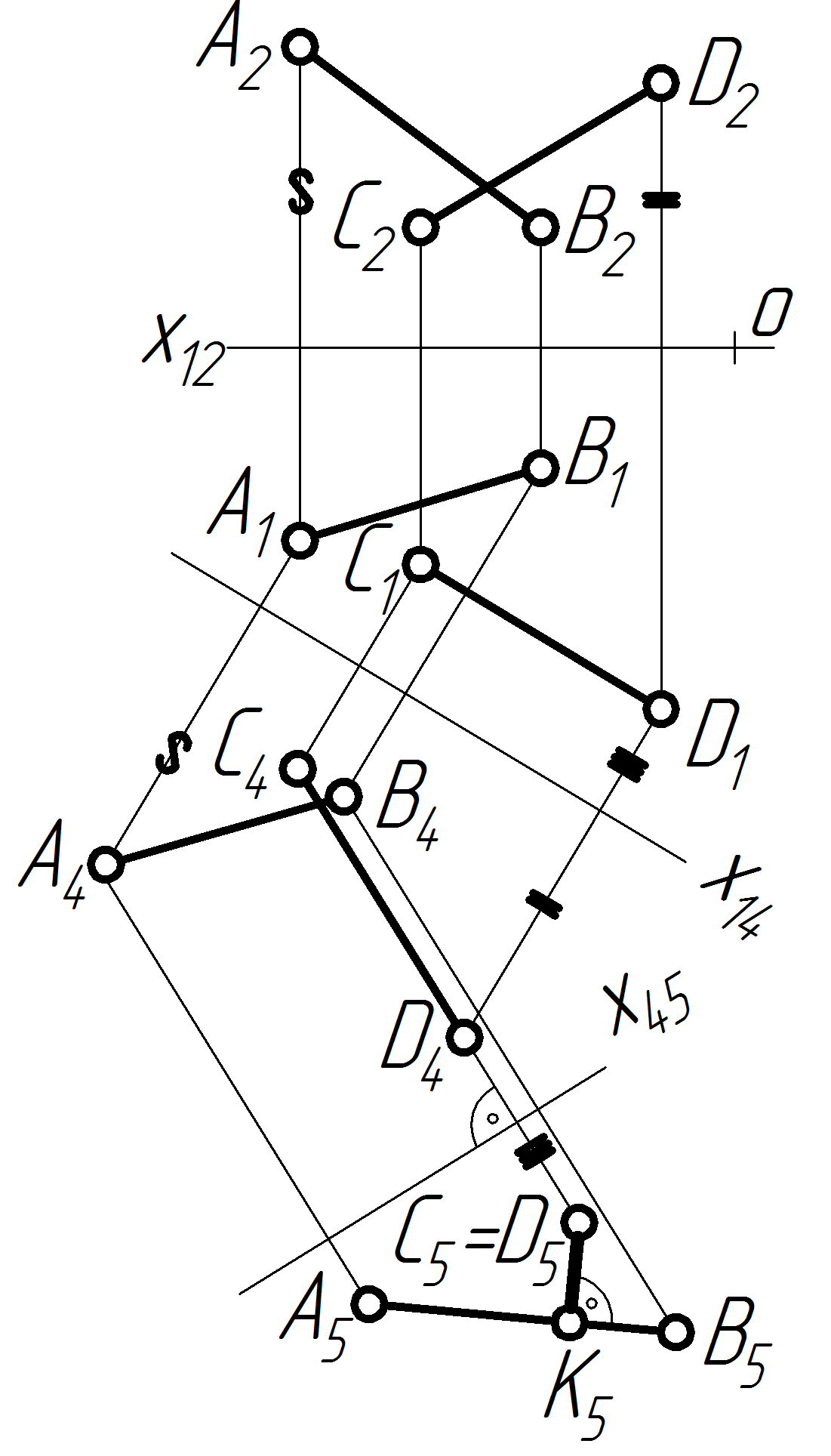
Щоб знайти відстань між двома мимобіжними відрізками, потрібно зробити дві заміни, так як і у попередній задачі.

Відрізок СD спроектувати у точку, а відрізок АВ у кожній новій системі буде проектуватися у відрізок.

Перпендикуляр, опущений з точки С₅D₅ на проекцію другого відрізка А₅В₅ і є шуканою відстанню між двома прямими.

Рисунок 2.36

Задача 22 Визначити дійсну величину трикутника АВС, який у системі ₂ - ₁ займає довільне положення (рис.2.37).

Відомо, що плоска фігура проектується в дійсну величину тоді, коли вона паралельна до будь-якої з площин проекцій. Однак розв’язати цю задачу заміною лише однієї площини проекцій неможливо.

Тому спочатку вводимо таку площину проекцій, до якої трикутник став би перпендикулярним(став проекційним), а потім проводимо заміну другої площини проекцій паралельно до площини трикутника АВС.

Щ об трикутник став проекційним до нової площини проекцій, використаємо одну з ліній особливого положення в трикутнику – горизонталь h(h₂;h₁), яку для зручності проводимо через вершину трикутника С. Спочатку замінимо площину ₂ на ₄, перпендикулярну до ₁ так, щоб нова вісь проекцій Х₁₄ стала перпендикулярною до горизонтальної проекції горизонталі h. Побудувавши фронтальну проекцію трикутника в системі ₁-₄, бачимо, що вершини трикутника АВС лежать на одній прямій, це означає, що трикутник став перпендикулярним до площини ₄, тобто він став фронтально-проекційним. Далі виконаємо другу заміну площин проекцій заміною площини ₁ на ₅, яка перпендикулярна до ₄ і так, щоб вона була паралельна до проекції трикутника А₄В₄С₄. Нарешті будуємо в системі ₄-₅ проекцію А₅В₅С₅ трикутника, яка і є його дійсною величиною. Побудову показано стрілками, а віддалі позначені умовними позначками.

Рисунок 2.37

Задача 23 Довільній площині  надати положення фронтально-проекційної

Д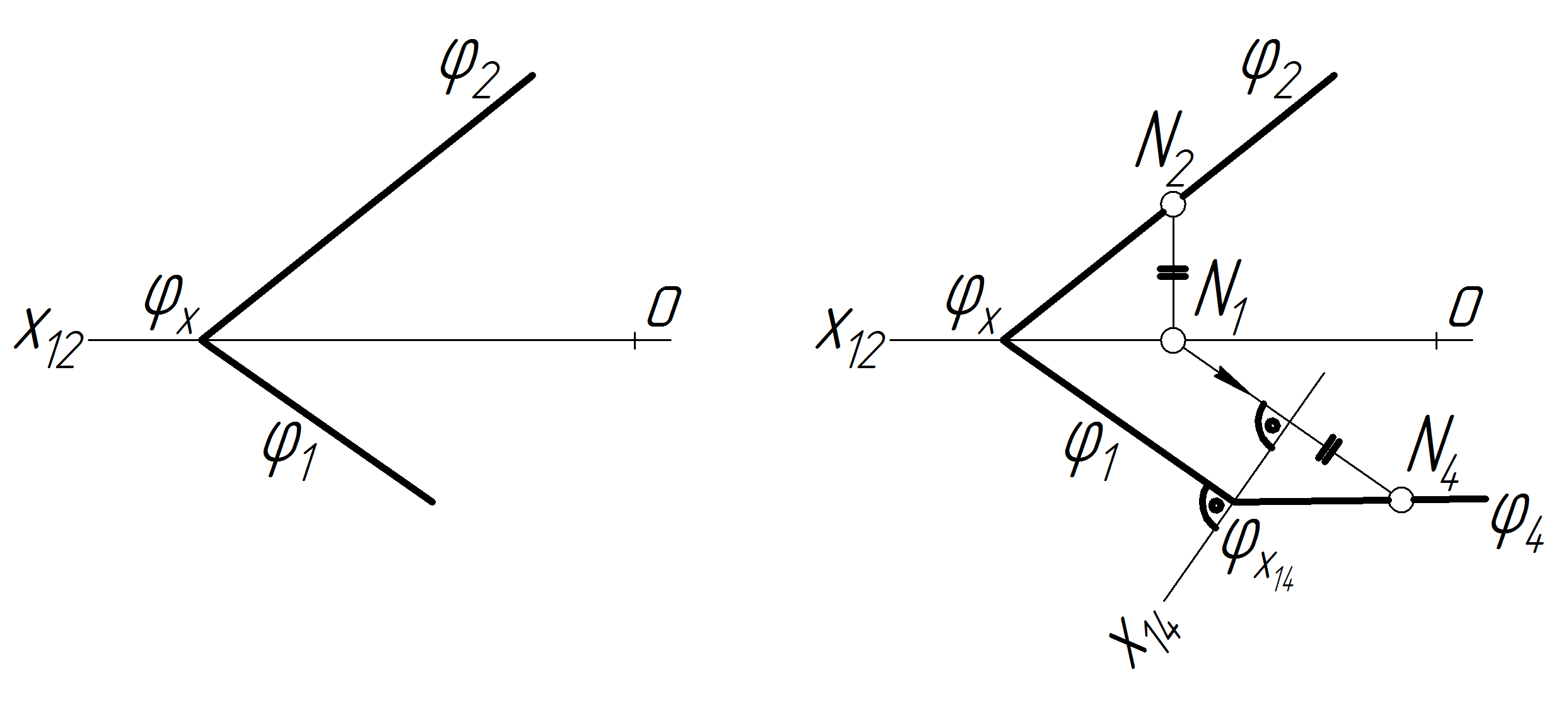 ля того, щоб площина  стала фронтально-проекційною, необхідно замінити фронтальну площину проекцій ₂ на ₄ таким чином, щоб вона була перпендикулярною не тільки до площини ₁, а й до площини j. у зв’язку з цим площина p₄ повинна бути перпендикулярною до лінії перетину площин j та p₁ , тобто до горизонтального сліду j₁ . Нова вісь проекцій Х₁₄ буде перепендикулярною до j₁ і точка j х₁₄ є новою точкою збігу слідів у системі p₄ - p₁. Для побудови горизонтального сліду j₄ беремо на j₂ будь-яку точкуN (N₂; N₁) і знаходимо її нову проекцію N₄ у новій системі p₄ - p₁. Через точку j х₁₄ і N₄ будуємо новий слід j₄ площини j (побудова показана стрілкою та умовною позначкою).

Рисунок 2.38

Задача 24 Знайти лінію перетину піраміди з площиною j

Д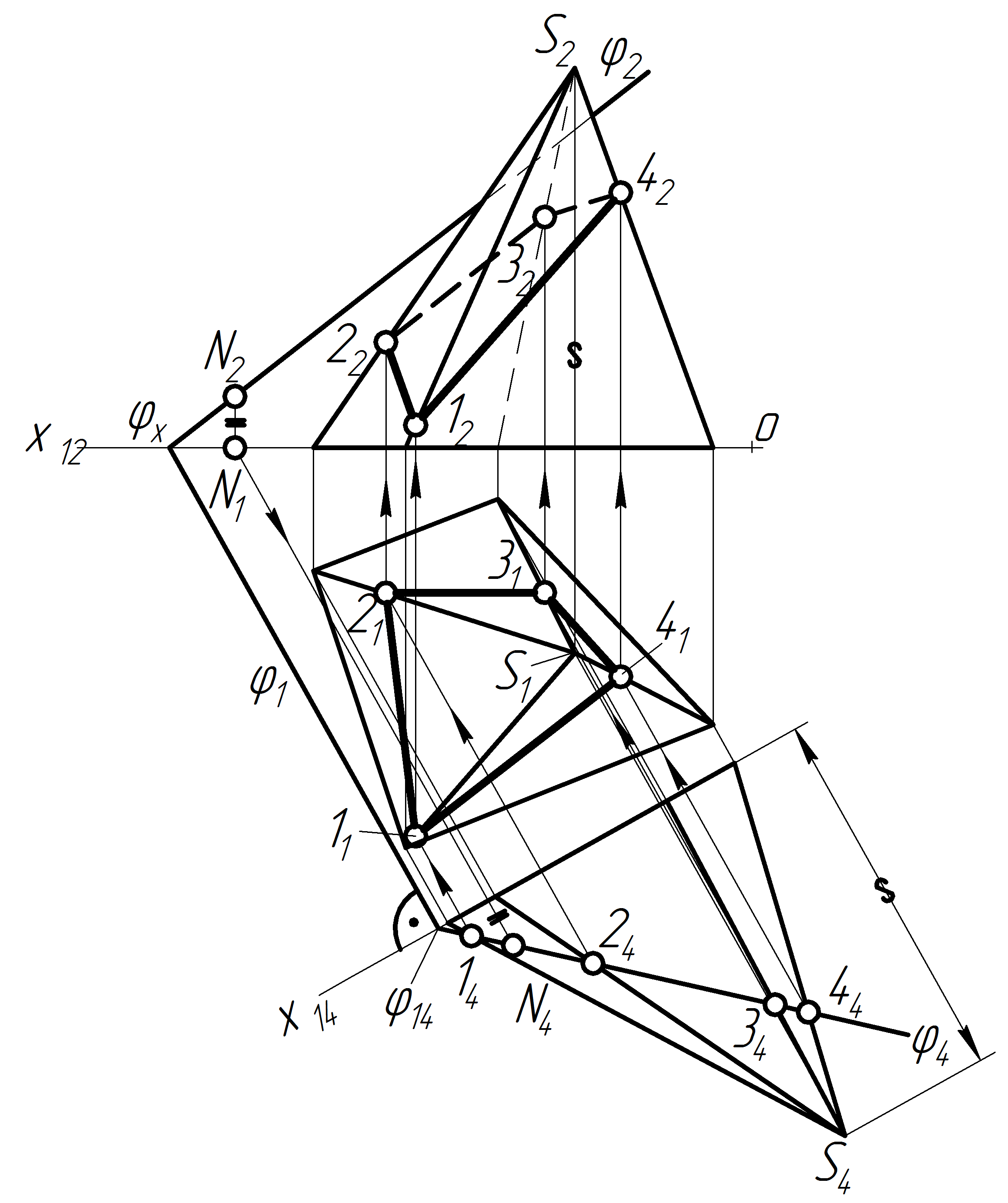 ля побудови лінії перетину потрібно шукати перетини бокових ребер піраміди з площиною j. Оскільки площина j — загального положення, доцільно замінити площину проекцій таким чином, щоб у новій системі площина j стала фронтально-проекційною, як у попередній задачі. Також у новій системі будуємо проекцію піраміди. На основі збираючої властивості проекційних площин знаходимо проекцію лінії перетину 1₄2₄3₄4₄ . зворотньою побудовою знаходимо горизонтальну проекцію лінії перетину 1₁2₁3₁4₁ та фронтальну поекцію 1₂2₂3₂4₂ (побудову показано стрілками).

Рисунок 2.39