Запитання та завдання для самоперевірки

1. Якими елементами може задаватися площина?

2. Як називається площина, розташована перпендикулярно:

а) до горизонтальної площини проекції; б) до фронтальної площини проекції?

3. Як називається площина, розташована паралельно:

а) до горизонтальної площини проекції; б) до фронтальної площини проекції?

4. Яку пряму називають горизонталлю площини; фронталлю площини?

5. Як проходить горизонтальна проекція горизонталі; фронтальна проекція горизонталі?

6. Як проходить горизонтальна проекція фронталі; фронтальна проекція фронталі?

7. Яку пряму називають лінією найбільшого нахилу площини до горизонтальної площини проекції; до фронтальної площини проекції?

8. Яке взаємне положення можуть займати пряма й площина; дві площини?

9. Чим визначається взаємна паралельність двох площин?

10. У чому суть загального способу побудови лінії перетину двох площин?

11. Яка ознака паралельності прямої й площини?

12. Яка послідовність побудов для знаходження точки перетину прямої з площиною? Як визначити “видимість” прямої у цьому разі?

13. Яка ознака перпендикулярності прямої й площини? Як на епюрі розміщуються проекції перпендикуляра до заданої площини?

14. На чому ґрунтується побудова двох взаємно перпендикулярних площин і які графічні операції треба виконати для цього?

15. Як будують на епюрі дві взаємно перпендикулярні прямі довільного положення?

16. Побудуйте довільний паралелограм, площина якого була б паралельна до площини довільного положення, заданої горизонтальним і фронтальним слідами.

17. Побудуйте лінію перетину двох площин довільного положення, горизонтальні та фронтальні сліди яких перетинаються в одній точці на осі ОХ.

18. Побудуйте точку перетину довільної прямої з профільно-проекційною площиною.

19. Побудуйте точку перетину довільної прямої з довільним трикутником.

20. Задайте дві довільні площини:

а) парою паралельних прямих; б) парою перетинних прямих.

Побудуйте лінію перетину цих площин, не визначаючи їх слідів.

21. Побудуйте лінію перетину двох довільних фігур — паралелограма і трикутника. Виділіть різними кольорами видимі їх частини.

22. Задайте довільну площину парою перетинних прямих і у точці перетину прямих

поставте до площини перпендикуляр довжиною 50 мм, не будуючи слідів площини.

23. Задані довільна площина Р і довільний відрізок АВ поза нею. Через відрізок АВ проведіть площину Q, перпендикулярну до площини Р.

24. Задайтесь довільною прямою l і точкою поза нею. Визначте відстань від точки до прямої.

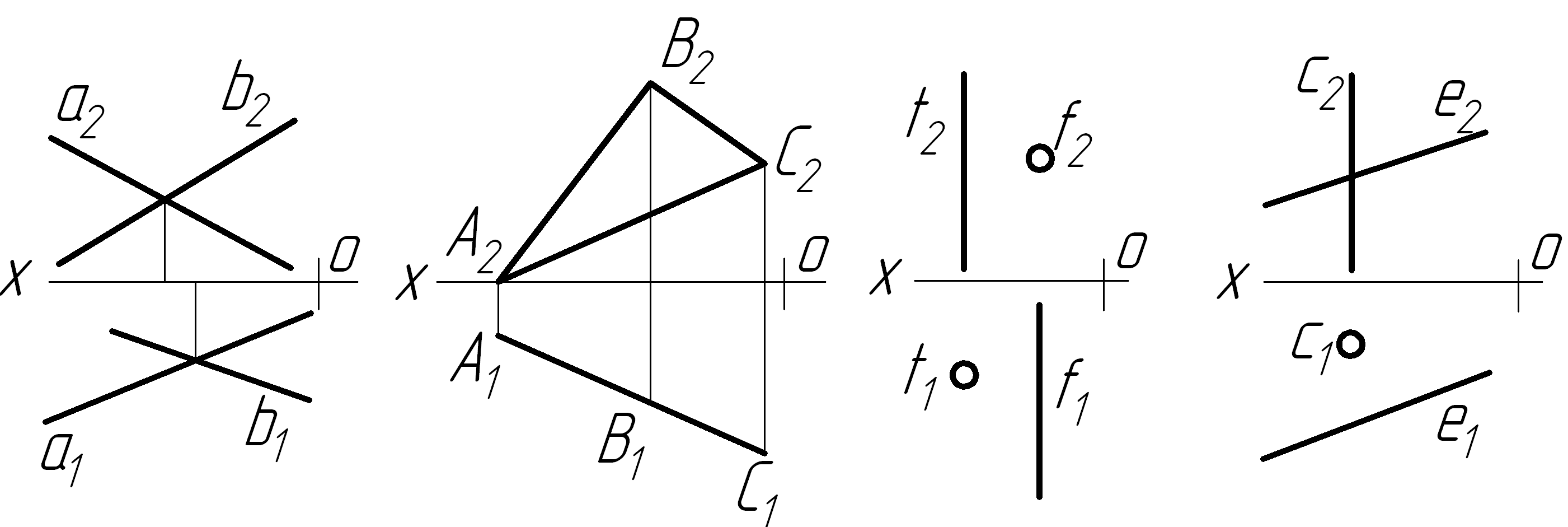25. Н а якому з рисунків задані лінії визначають площину?

а) б) в) г)

26. В 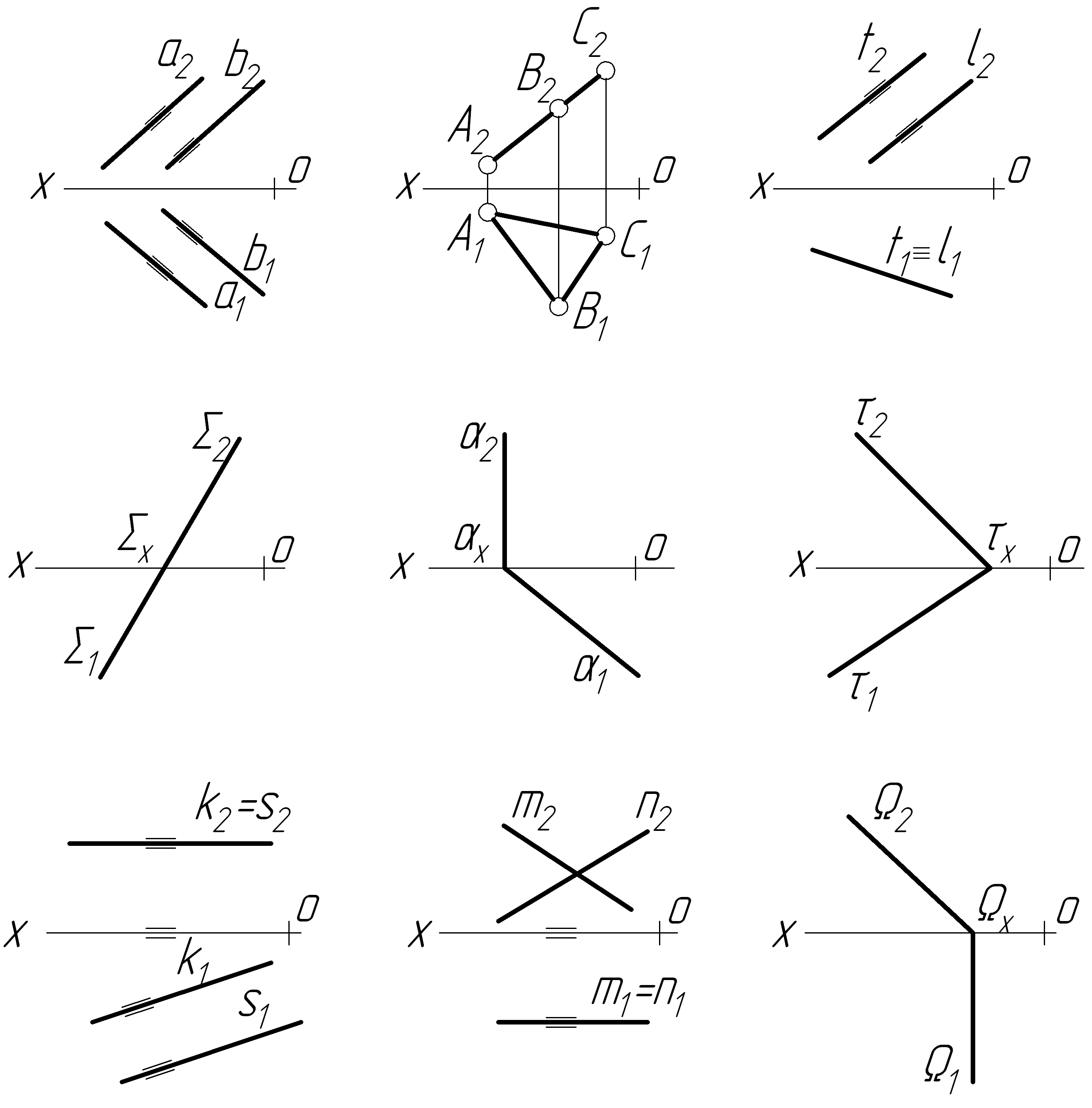казати положення в просторі і назву площин.

а) б) в)

г) д) е)

є) ж) з)

26. Н 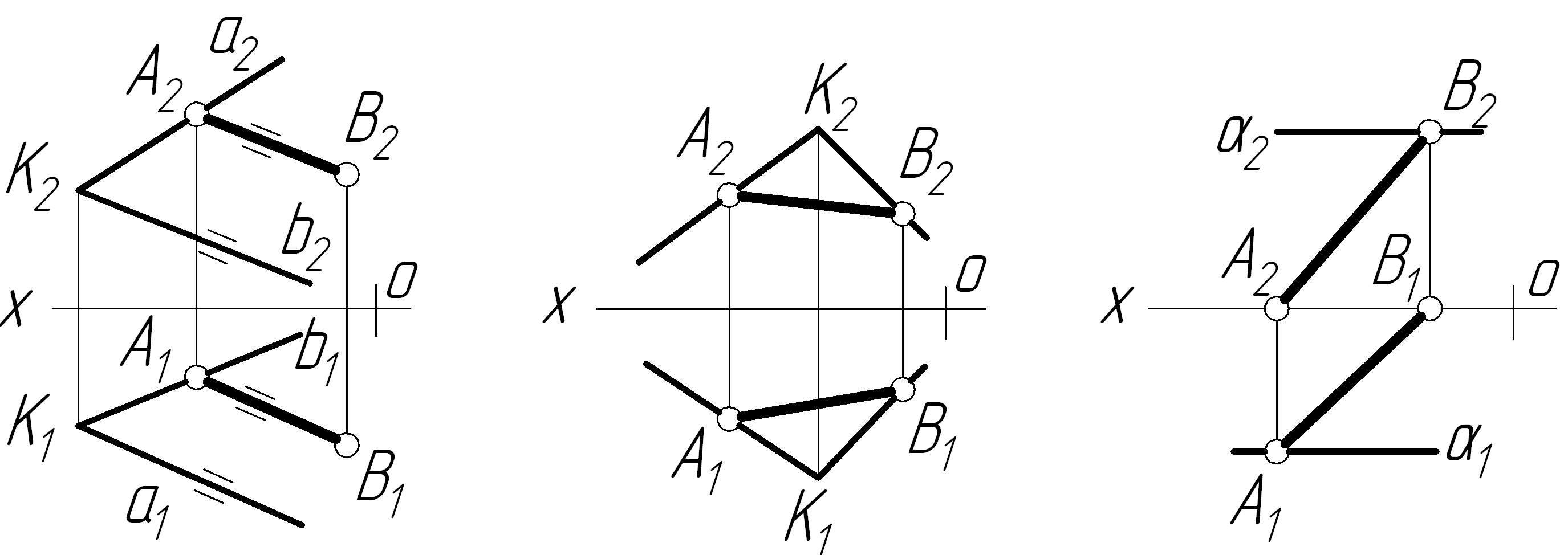а якому з рисунків відрізок АВ не належить заданій площині?

а) б) в)

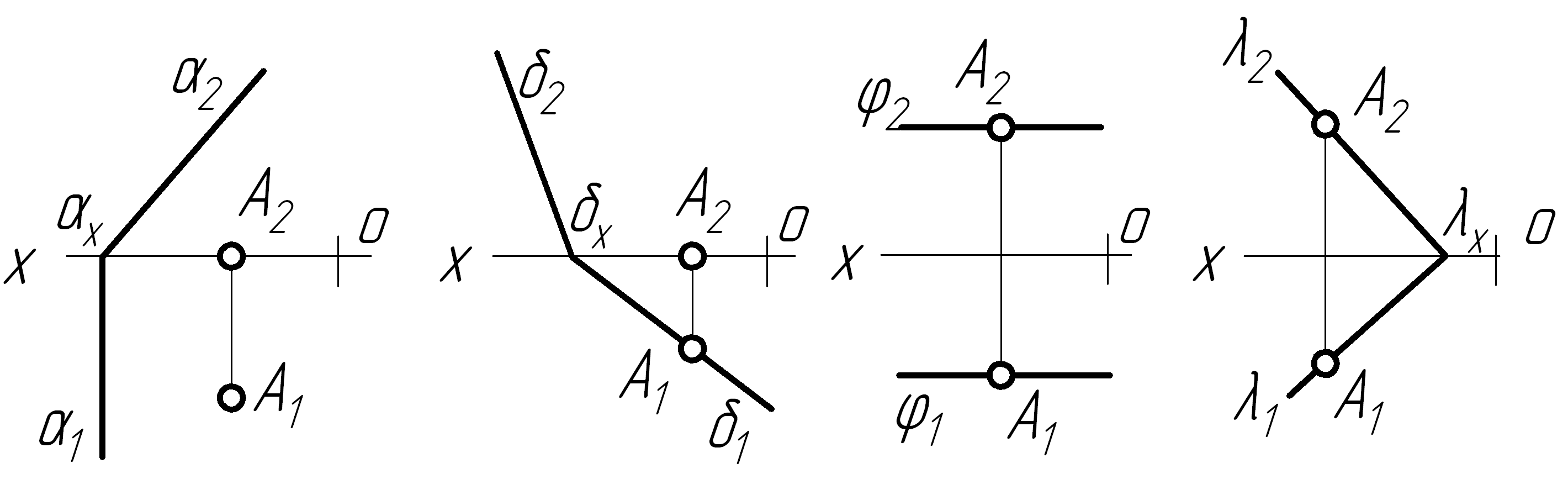26. Н а якому рисунку точка А належить площині?

а) б) в) г)

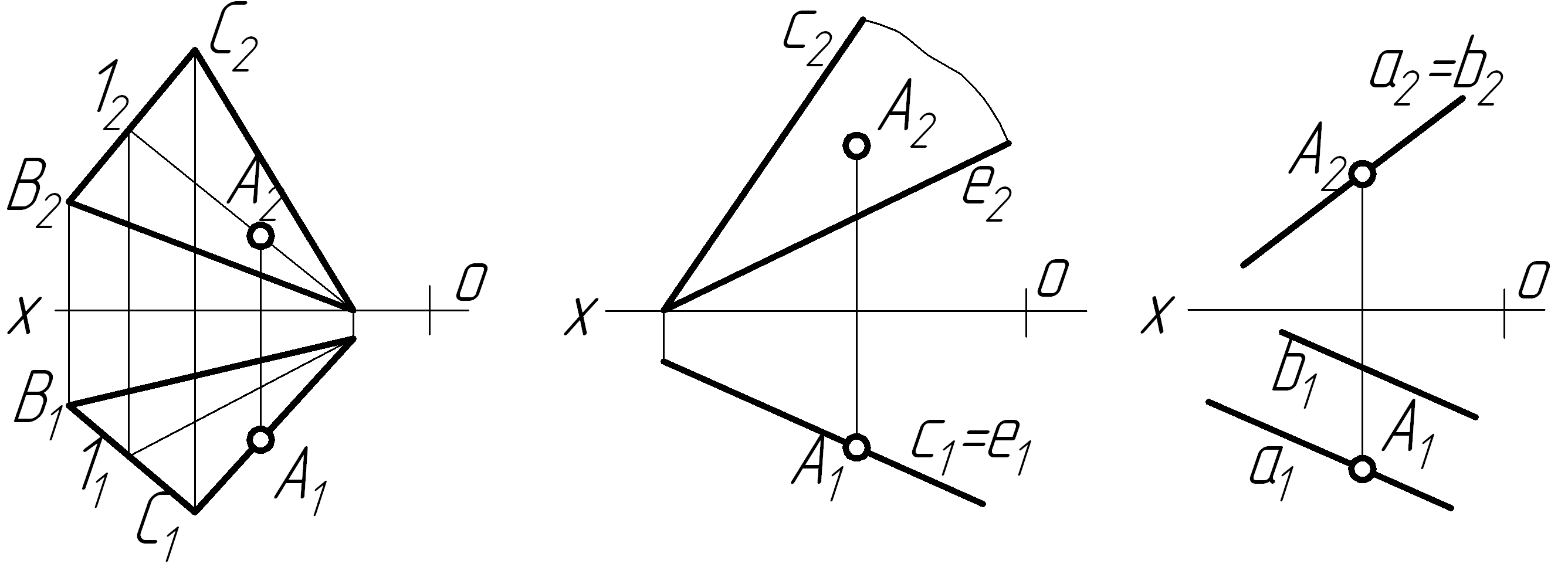26. Н а якому рисунку точка А не належить площині?

а) б) в)