1. Горизонатльна проекція ─ під прямим кутом до горизонтальної проекції горизонталі або до горизонтального сліду площини(рис. 2.18,б);

2. Фронтальна проекція ─ під прямим кутом до фронтальної проекції фронталі або до фронтального сліду площини (рис. 2.18,б);

3. Профільна проекція ─ під прямим кутом до профільної проекції профільної прямої або до профільного сліду площини.

Справедливе і обернене твердження, а тому, якщо площина перпендикулярна до прямої, то горизонтальний слід площини або горизонтальна проекція горизонталі перпендикулярна до горизонтальної проекції прямої, а фронтальний слід і фронтальна проекція фронталі площини перпендикулярні до фронтальної проекції прямої.

Використання перпендикуляра дозволяє розв’язувати різноманітні метричні задачі. Зокрема, віддаль від точки до прямої є відрізком перпендикуляра, проведеного з точки до прямої; віддаль від точки до площини вимірюється відрізком перпендикуляра, опущеного з точки до площини; віддаль між паралельними площинами вимірюється відрізком перпендикуляра між ними.

приклади розв’язку задач

З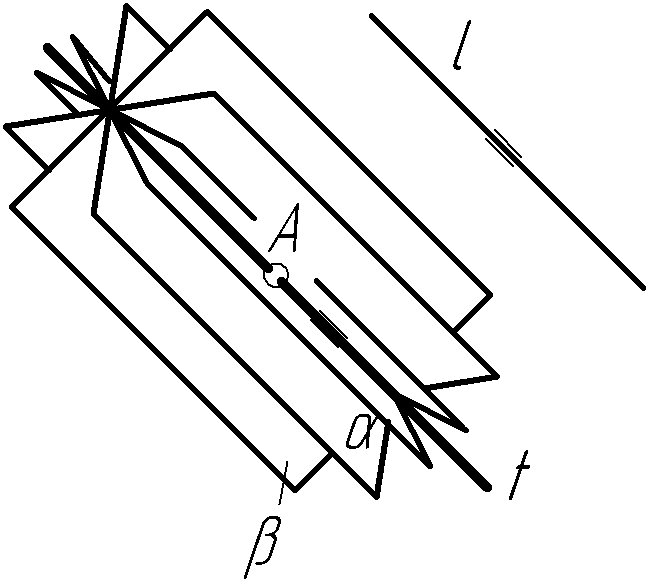 адача 7 Через задану точку провести площину паралельно до заданої прямої (рис. 2.19).

З

Рисунок 2.19

розуміло, що в цьому випадку через деяку точку А, можна провести жмут площин (, ,...), вісь яких є пряма t, що проходить через точку А паралельно до прямої l (рис.2.19). Щоб мати єдиний розв’язок, треба задати будь-яку додаткову умову. У даному випадку нехай це буде точка сходу слідів _Х. Проводимо через точку А пряму t паралельно до прямої l. Пряма t є віссю жмуту площин, які можна провести через точку А паралельно до прямої l (рис.2.19).

О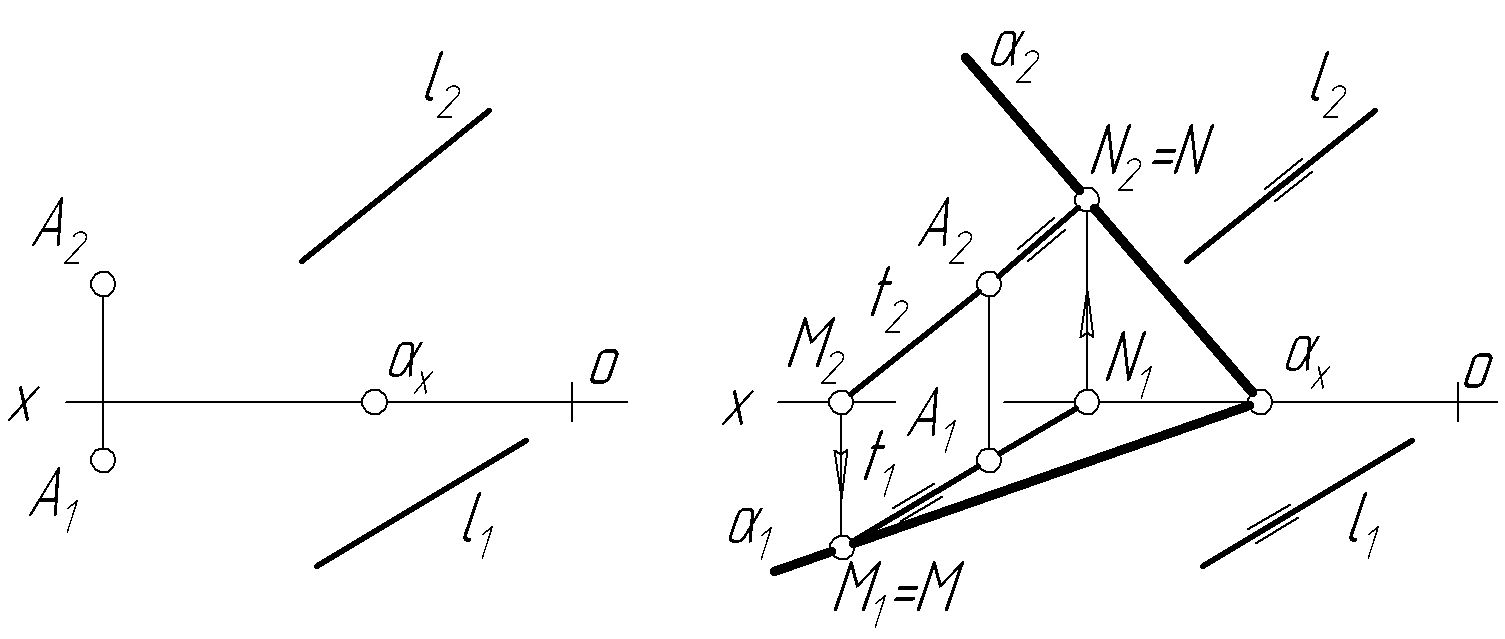 дну з цих площин, а саме шукану , можна провести виходячи з того, що сліди такої площини повинні пройти через однойменні сліди прямої t. Тому знаходимо сліди прямої t M=M₁ i N=N₂. Через ці точки і точку сходу слідів, яка задана, проводимо сліди площини ₂ і ₁. Площина  проходить через точку А і паралельна до прямої l.

Рисунок 2.20

Задача 8 Побудувати точку перетину прямої l з площиною, яка задана двома паралельними прямими m i n. Площину вважати непрозорою (рис.2.21).

Ч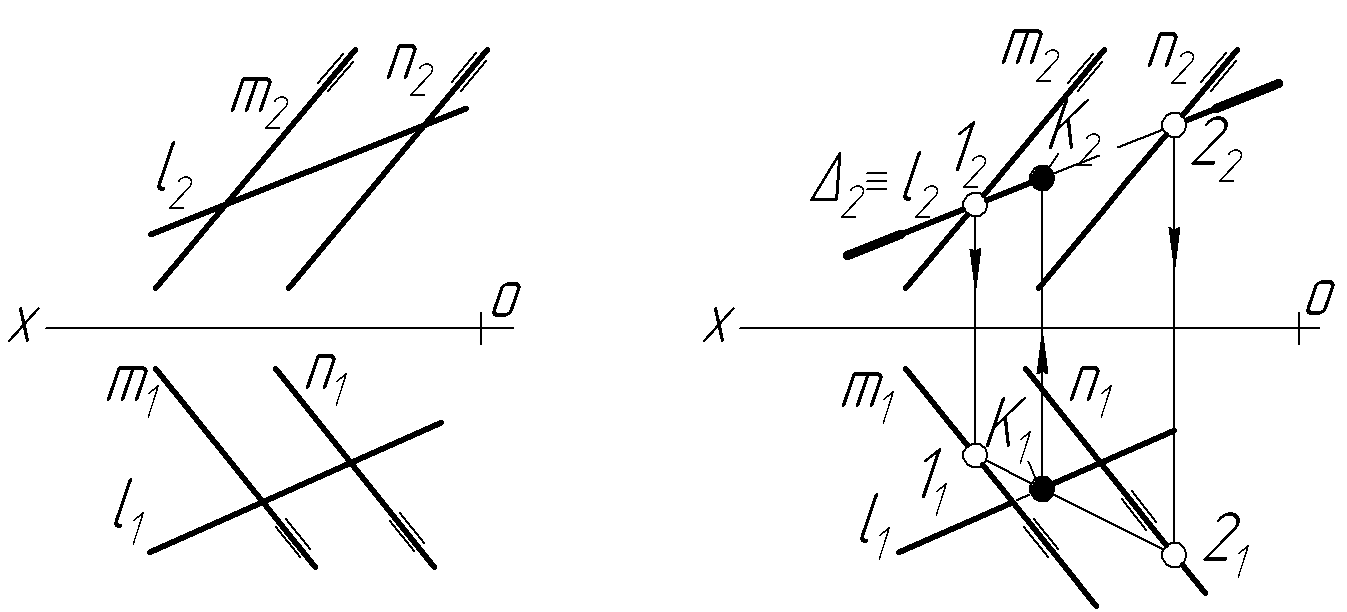 ерез пряму l (рис. 2.21,б) проводимо фронтально-проекційну площину Δ. Зображено тільки її фронтальний слід Δ₂ (горизонтальний слід Δ₁ у побудові участі не приймає). Побудовано лінію 12 перетину площини Δ із заданою площиною. На перетині 12 і АВ одержимо шукану точку К. Методом конкуруючих точок знаходимо видимість прямої відносно площини.

Рисунок 2.21

а) б)

Задача 9 Побудувати перетин прямої l з площиною, що задана двома перетинними прямими (рис.2.22).

У даному випадку пряма l особливого положення – фронтально-проекційна.

У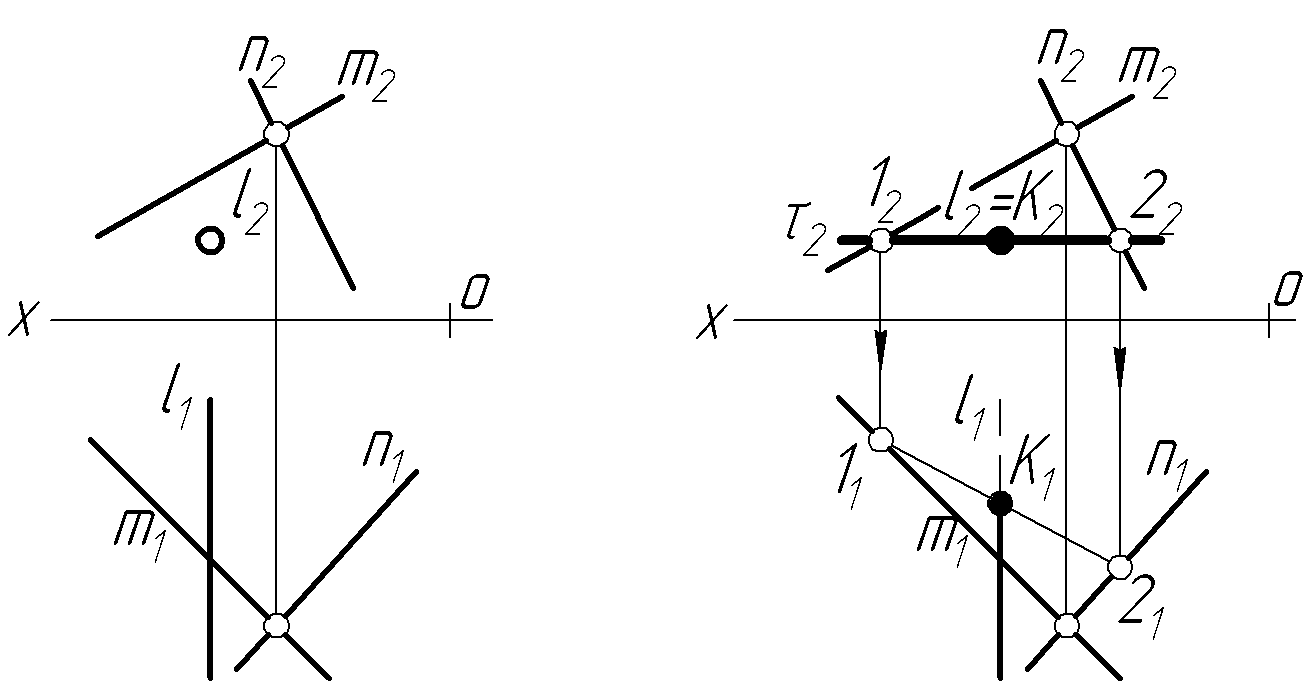 зв’язку з цим, відразу відомо, що l₂К₂ – фронтальна проекція прямої співпадає з фронтальною проекцією лінії перетину (збираюча властивість) (рис.2.22,б). Тому проводимо допоміжну горизонтальну площину  через l₂. Знаходимо лінію перетину допоміжної площини  із заданою площиною ─ це пряма 12(1₂2₂;1₁2₁). Знаходимо точку перетину К ─ вірніше, її горизонтальну проекцію К₁. Фронтальна проекція К₂ лежить на ₂ і співпадає з l₂.

а) б)

Рисунок 2.22

Задача 10 Побудувати перетин прямої l з площиною, заданою трикутником, і визначити видимість прямої відносно площини трикутника. Площину АВС вважати непрозорою (рис.2.23).

З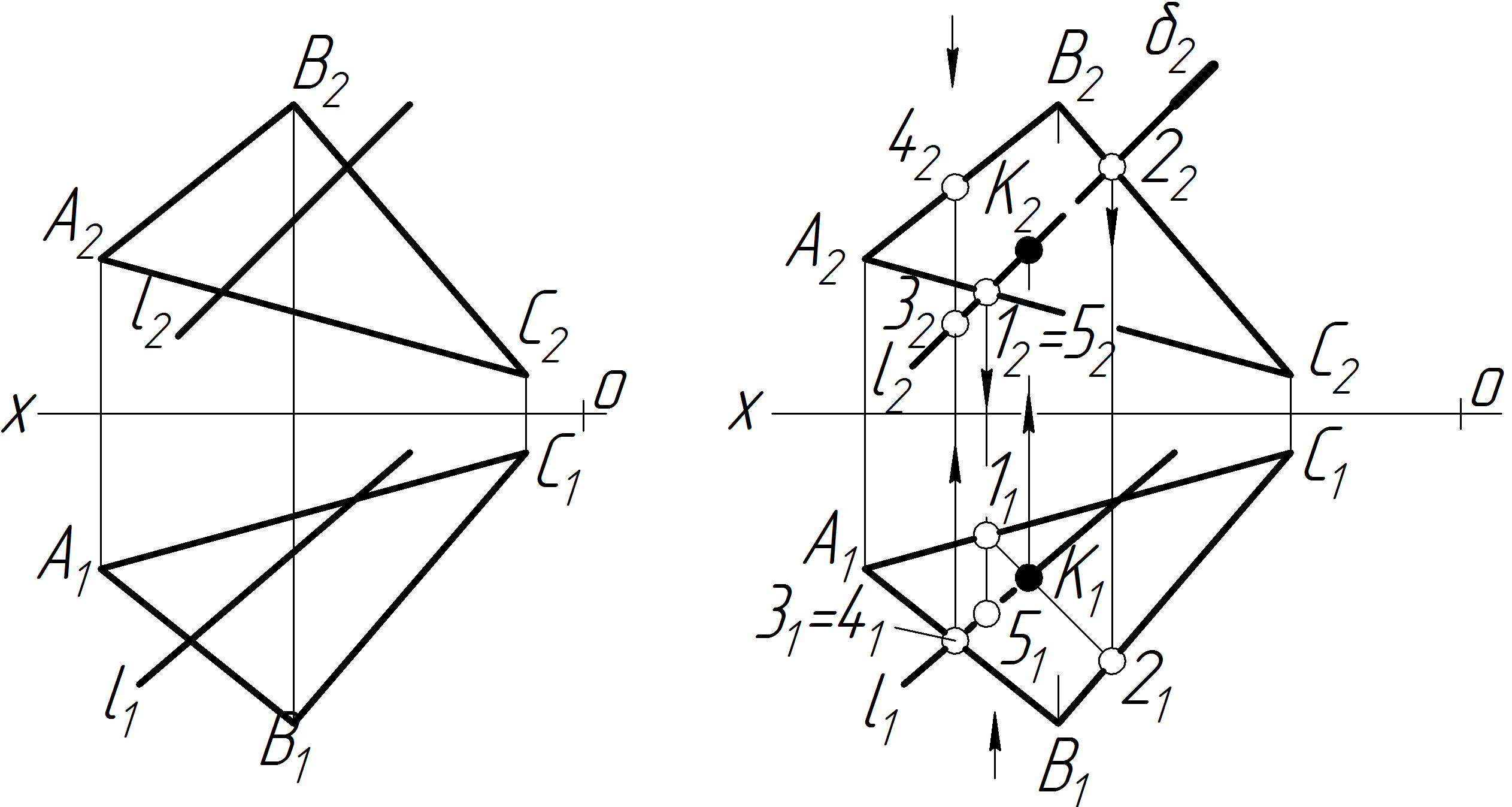 а аналогією розв’язку попередніх задач знаходимо точку К (рис.2.23,б). Видимість визначаємо за допомогою методу конкуруючих точок 1-2 і М-3.

а)

б)

Рисунок 2.23

Розглянувши спосіб знаходження точки перетину прямої з площиною, можна перейти до побудови лінії перетину плоских фігур, якщо одна із них задана не слідами, або обидві площини задані не слідами. Зрозуміло, що можна було б попередньо побудувати сліди таких площин, а потім визначити лінію їх перетину, користуючись викладеними раніше міркуваннями і способами. Однак, у таких випадках побудова лінії перетину двох площин цілком можлива без знаходження слідів площини. Слід зазначити, що в таких задачах можна знайти лінію перетину, використавуючи метод посередників, однак цей метод ускладнює побудову.

Задача 11 Побудувати лінію перетину трикутника АВС з площиною, заданою двома паралельними прямими k i s (рис.2.24).

Побудова лінії перетину MN у цій задачі зводиться до знаходження точок M i N, які є точками перетину прямих k i s з площиною трикутника АВС, і побудови через ці точки відрізка прямої лінії, що буде лінією перетину двох площин. Точку N знайдемо як точку перетину прямої s з площиною трикутника АВС (рис. 2.24,б). Для цього через пряму s проведемо допоміжну горизонтально-проекційну площину . Площина  перетинає трикутник АВС по прямій 12(1₁2₁;1₂2₂). На фронтальній проекції знаходимо N₂, як результат перетину s₂ з 1₂2₂. За лінією проекційного зв’язку на s₁ знаходимо N₁. Отже, знайдемо точку N(N₂;N₁).

Аналогічно знаходимо точку M(M₂;M₁) (рис.2.24,в). Точка М – це точка перетину прямої k з площиною трикутника АВС. Для цього через пряму k проводимо допоміжну площину . Площина  перетинає трикутник АВС по лінії 34(3₁4₁;3₂4₂). На перетині k₂ з 3₂4₂ знаходимо М₂. За лінією проекційного зв’язку на k₁ знайдемо M₁ , з’єднуємо точки N і М і дістанемо шукану лінію перетину заданих площин. Вважаючи площини непрозорими, визначаємо видимість першої відносно другої за допомогою конкуруючої пари точок 3-5; 6-7 (рис. 2.24,г).

П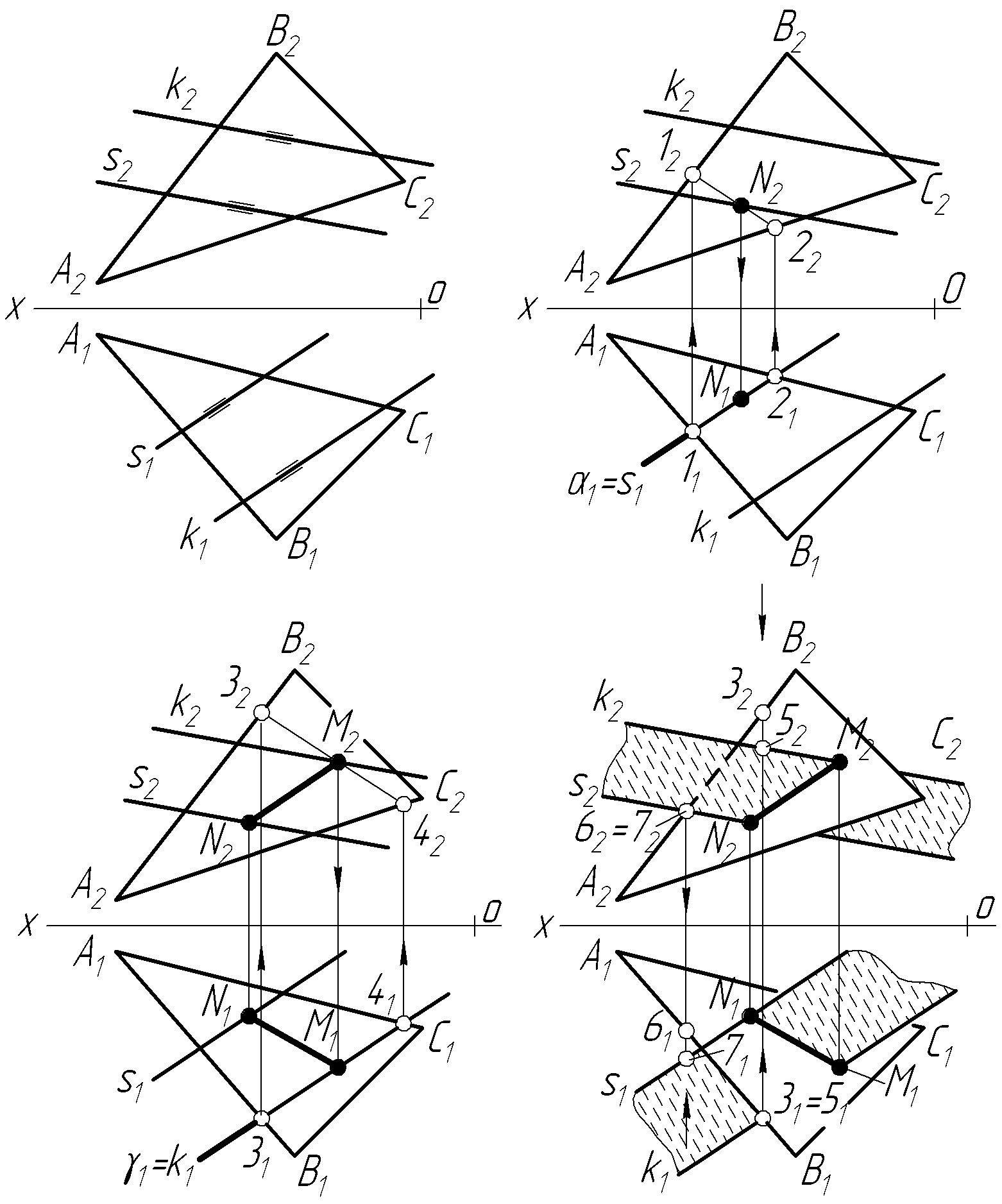 обудова лінії перетину двох площин значно спрощується, якщо одна із площин є проекційною.

а) б)

в) г)

Рисунок 2.24

Задача 12 Визначити відстань від точки А до площини  (рис.2.25).

Н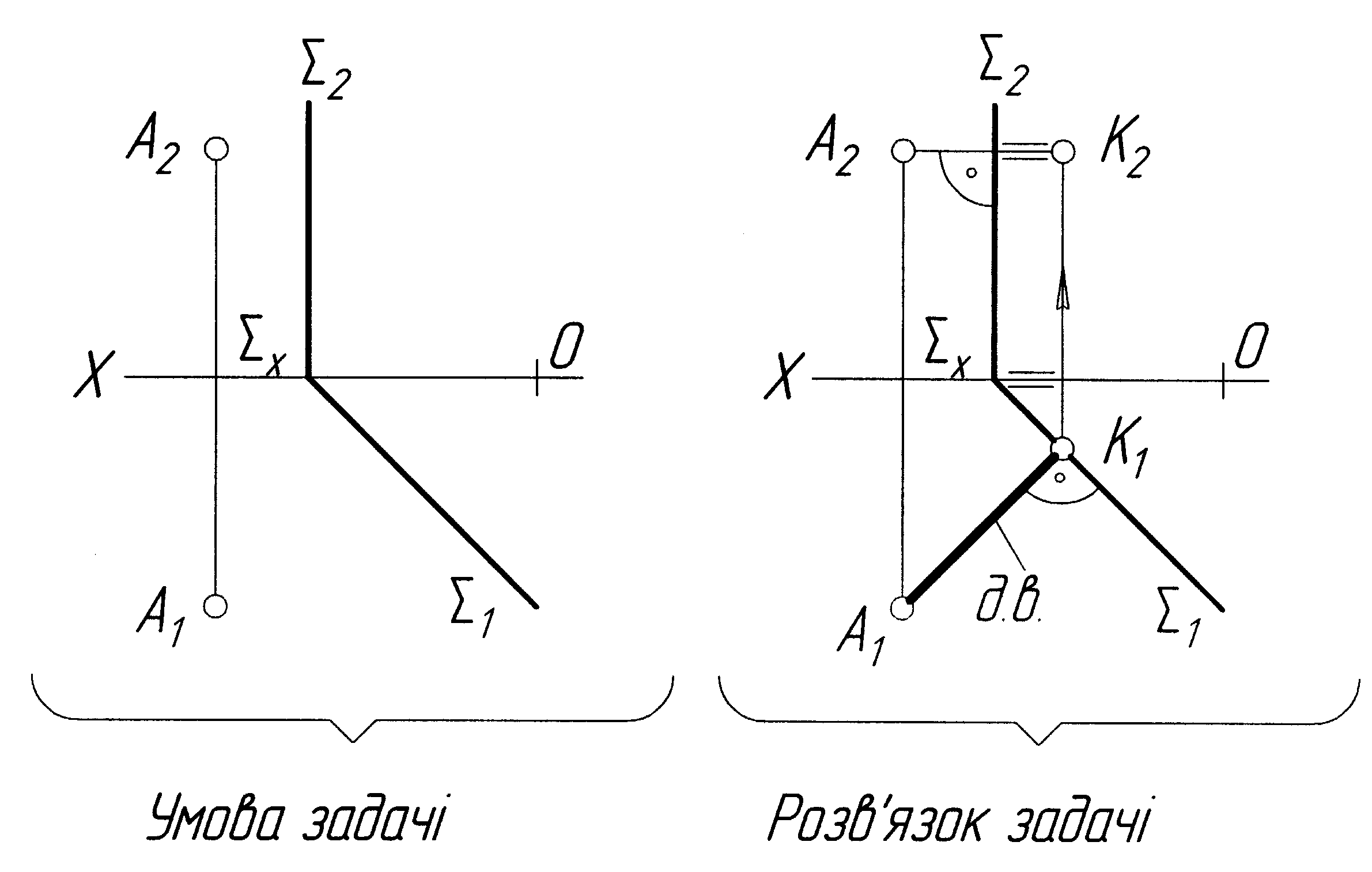 айкоротша відстань від точки А до площини виміряється перпендикуляром. На основі викладеного вище, проекції перпендикуляра пройдуть через точку А перпендикулярно слідам площини. Основою перпендикуляра – точкою перетину перпендикуляра з площиною, є точка К. Її горизонтальну проекцію К₁ знаходимо за збираючою властивістю проектуючої площини, а К₂ ─ по лінії проекційного зв’язку на фронтальній проекції перпендикуляра А₂К₂. А₁К₁ – дійсна величина відстані від точки А до площини, бо фронтальна проекція А₂К₂ розміщена паралельно до горизонтальної площини проекцій (АК — горизонтальний відрізок).

Рисунок 2.25

Задача 13 Знайти дійсну величину відстані від точки А до площини .

В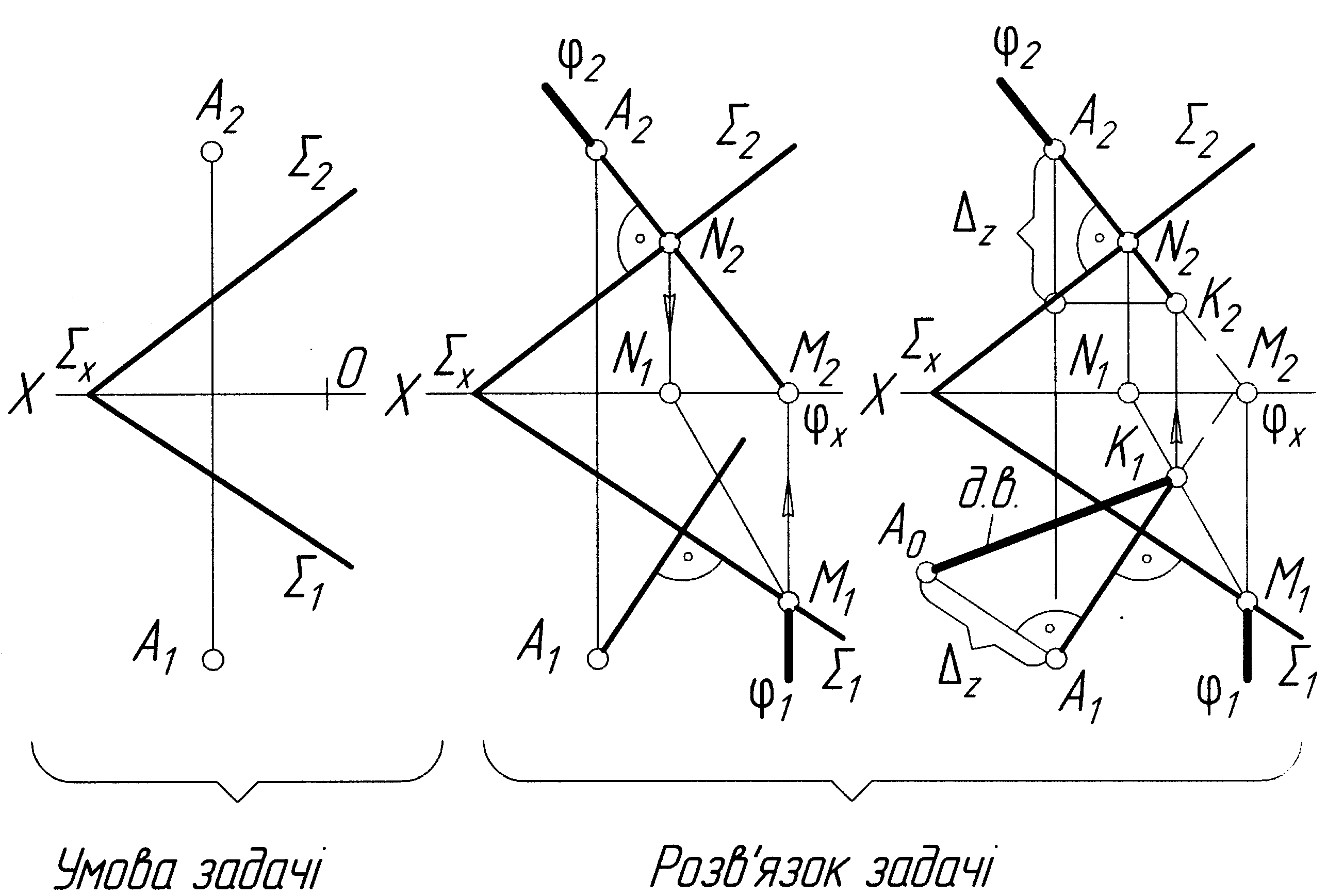 ідомо, що відстань від точки до площини вимірюється відрізком перпендикуляра від заданої точки до основи перпендикуляра – точки перетину перпендикуляра з площиною. Для цього з точки А проводимо перпендикуляр (рис. 2.26) до площини. Фронтальна проекція пройде через А₂ перпендикулярно до ₂, горизонтальна проекція ─ через А₁ перпендикулярно до _1. Основу перпендикуляра, точку К, знаходимо як точку перетину прямої (перпендикуляра) з площиною. Знайшовши відстань у проекціях А₂К₂ і А₁К₁, знаходимо дійсну величину АК, використовуючи правило прямокутного трикутника. А₀К₁ – дійсна величина відстані від точки А до площини .

Рисунок 2.26

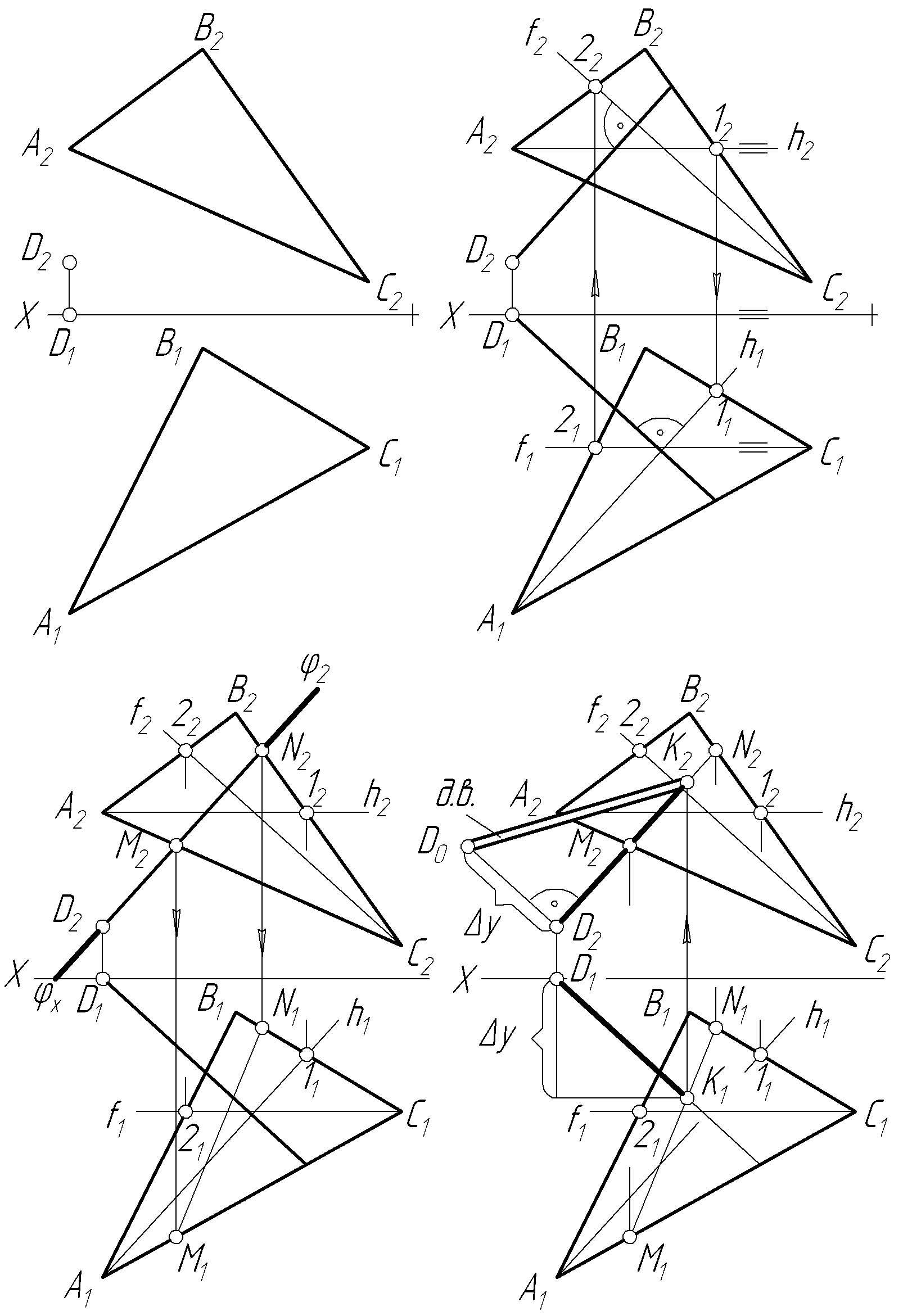
Задача 14 Знайти дійсну величину відстані від точки D до трикутника АВС (рис. 2.27).

Для того, щоб провести проекції перпендикуляра, у трикутнику АВС будуємо насамперед горизонталь h через вершину А і фронталь f через вершину С. Потім з проекцій точки D проводимо проекції перпендикуляра: з точки D₁ ─ перпендикулярно до h₁ і із точки D₂ ─ перпендикулярно до f₂ (рис. 2.27,б). Далі через перпендикуляр проводимо допоміжну, фронтально-проекційну площину . Будуємо лінію перетину заданої площини трикутника АВС з допоміжною площиною  - це буде лінія MN(M₂N₂;M₁N₁). І нарешті, знаходимо основу перпендикуляра точку К(К₂,К₁). Відстань від точки D до трикутника АВС знайдено в проекціях D₂K₂ і D₁K₁. Дійсну величину D₀K₂ знаходимо, використовуючи правило прямокутного трикутника (2.27,г).

а) б)

в) г)

Рисунок 2.27

Задача 15 З точки А, що належить площині , побудувати перпендикуляр довжиною 35 мм (рис.2.28).

Точка А, яка належить площині , задана своєю фронтальною проекцією. Знаходимо її горизонтальну проекцію за допомогою горизонталі h. Далі з точки А(А₂,А₁) виставляємо проекції перпендикуляра: через А₂ перпендикулярно до ₂, а через А₁ перпендикулярно ₁. Обмежуємо цей перпендикуляр довільною точкою 1(1₂,1₁). Методом прямокутного трикутника знаходимо дійсну величину обмеженої частини перпендикуляра А₂1₀. На дійсній величині від точки А₂ відкладаємо 35 мм. Одержимо точку В₀. З побудови на рисунку 2.28 видно, як знаходили проекції В₂ і В₁ (показано стрілками). Отже, А₂В₂ і А₁В₁ – проекції перпендикуляра, який виставлено з площини , дійсна величина його дорівнює 35 мм.

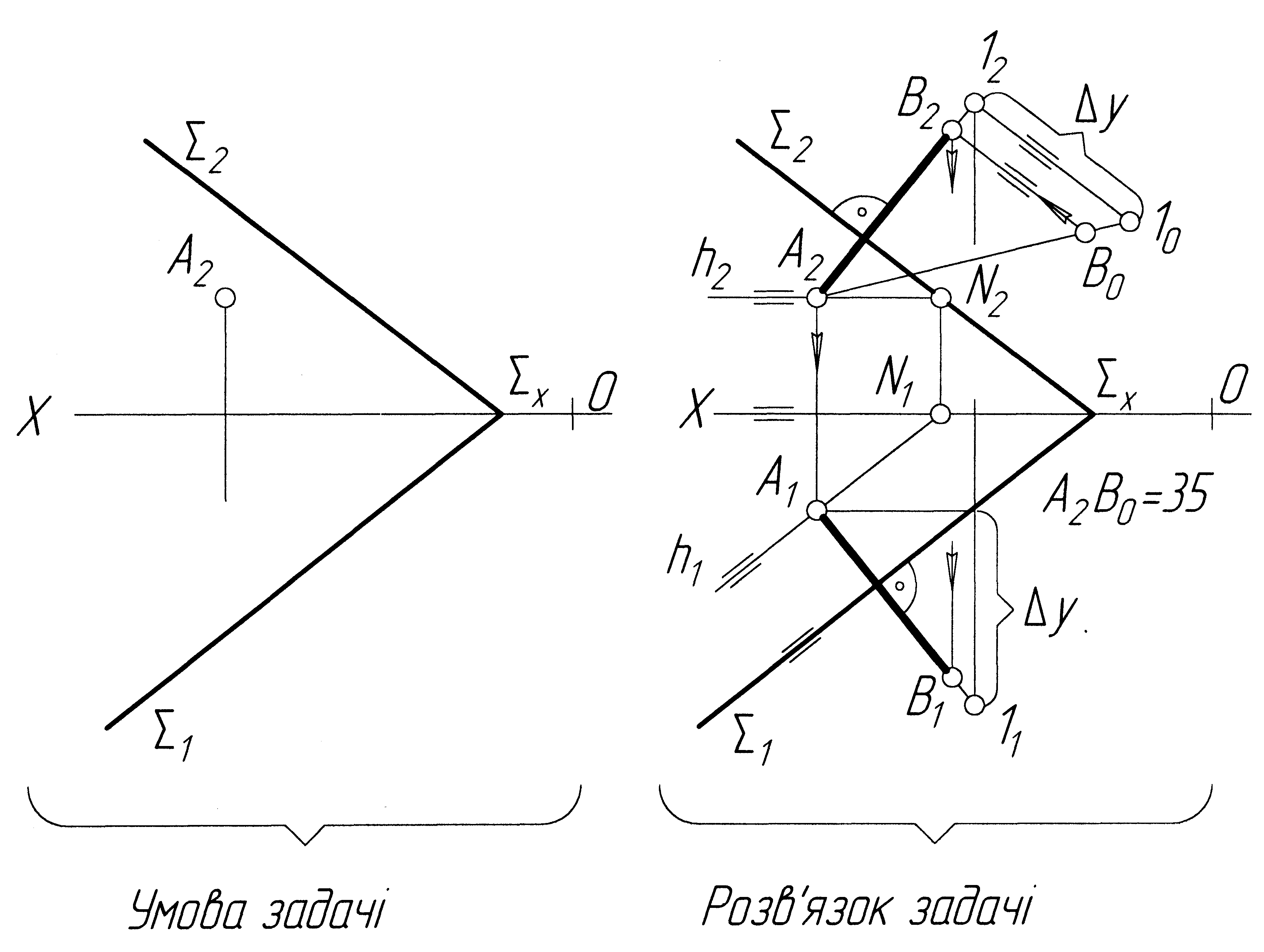
Рисунок 2.28

Задача 16 Визначити відстань від заданої точки А до прямої загального положення l (рис.2.29).

Відстань від точки до прямої вимірюється відрізком перпендикуляра, опущеного з точки на пряму. Для побудови через точку А проводимо допоміжну, перпендикулярну до прямої l, площину . Задаємо її двома прямими, що перетинаються в точці А, а саме горизонталлю і фронталлю. Оскільки площина має бути перпендикулярною до прямої l, то h₁l₁, а f₂l₂. Далі знаходимо точку К(К₂К₁) – точку перетину l з площиною . Для цього через пряму l проводимо допоміжну фронтально-проекційну площину . Знаходимо лінію перетину 12(1₂2₂;1₁2₁) площини  з площиною . На перетині 1₁2₁ з l знаходимо К₁ по лінії проекційного зв’язку на l₂ знаходимо К₂. АК(А₂К₂;А₁К₁) – відстань від точки А до прямої l. А₀К₁ — дійсна величина відстані, знайдена методом прямокутного трикутника.

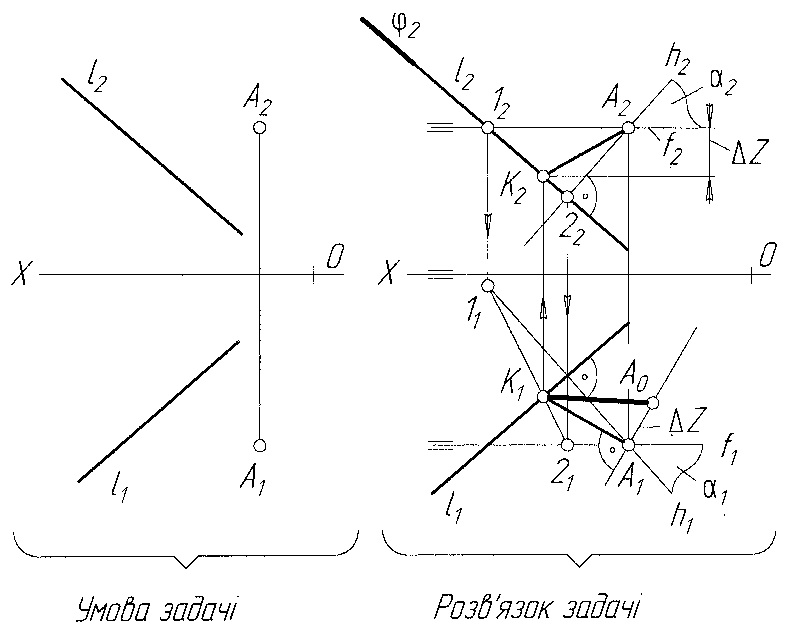
Рисунок 2.29

В результаті вивченого та закріпленого на розглянутих вище прикладах матеріалу, студент вправі розв'язати складні, комплексні задачі.

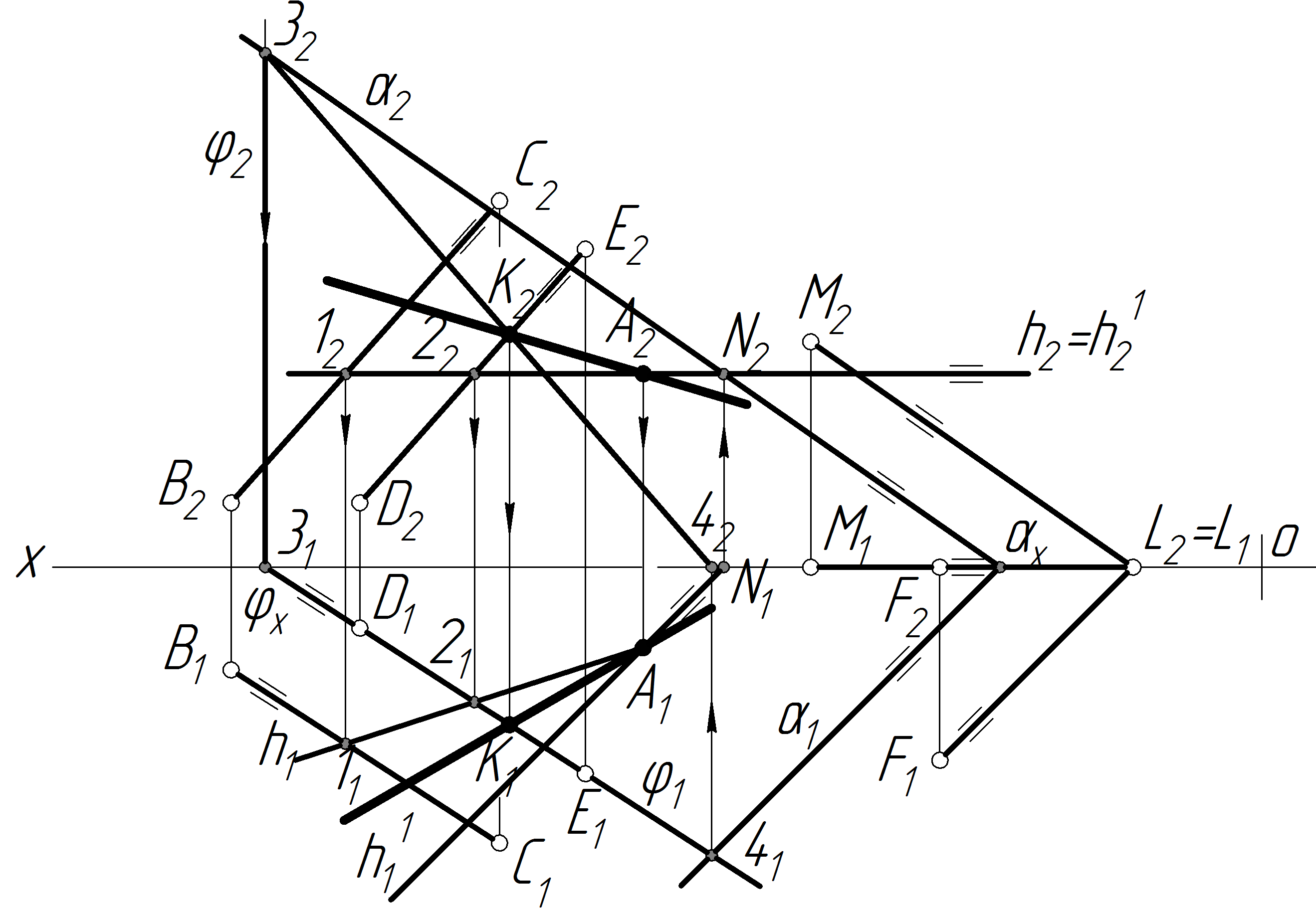
Задача 17 Задано площину Q (ВС||DЕ) і площину  (LMLN), а також точку А, яка належить площині Q . Провести у площині Q через точку А пряму, яка паралельна площині  .

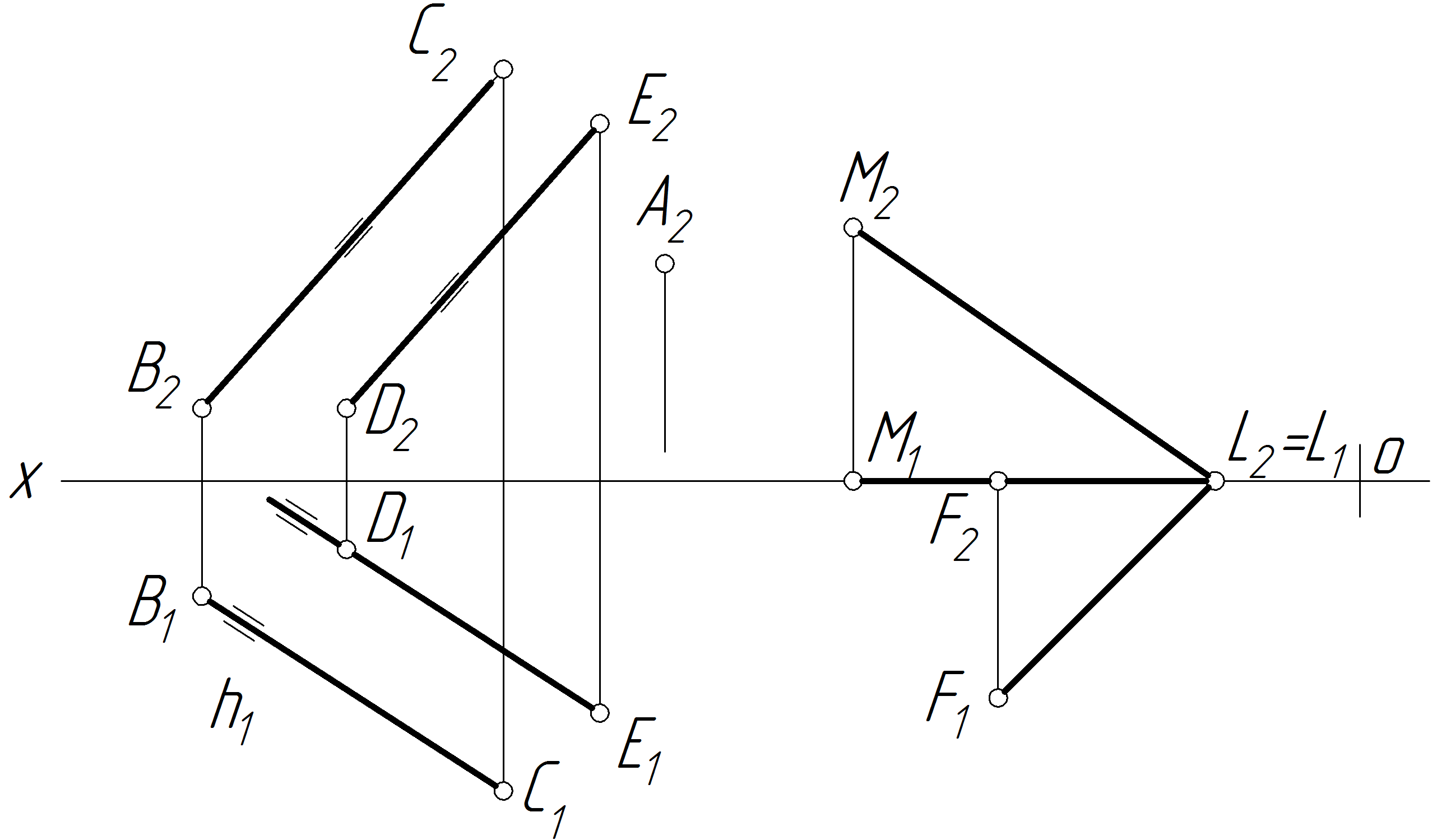
Рисунок 2.30 — Графічна умова задачі

План розв'язку

1. Знайти відсутню проекцію точки А.

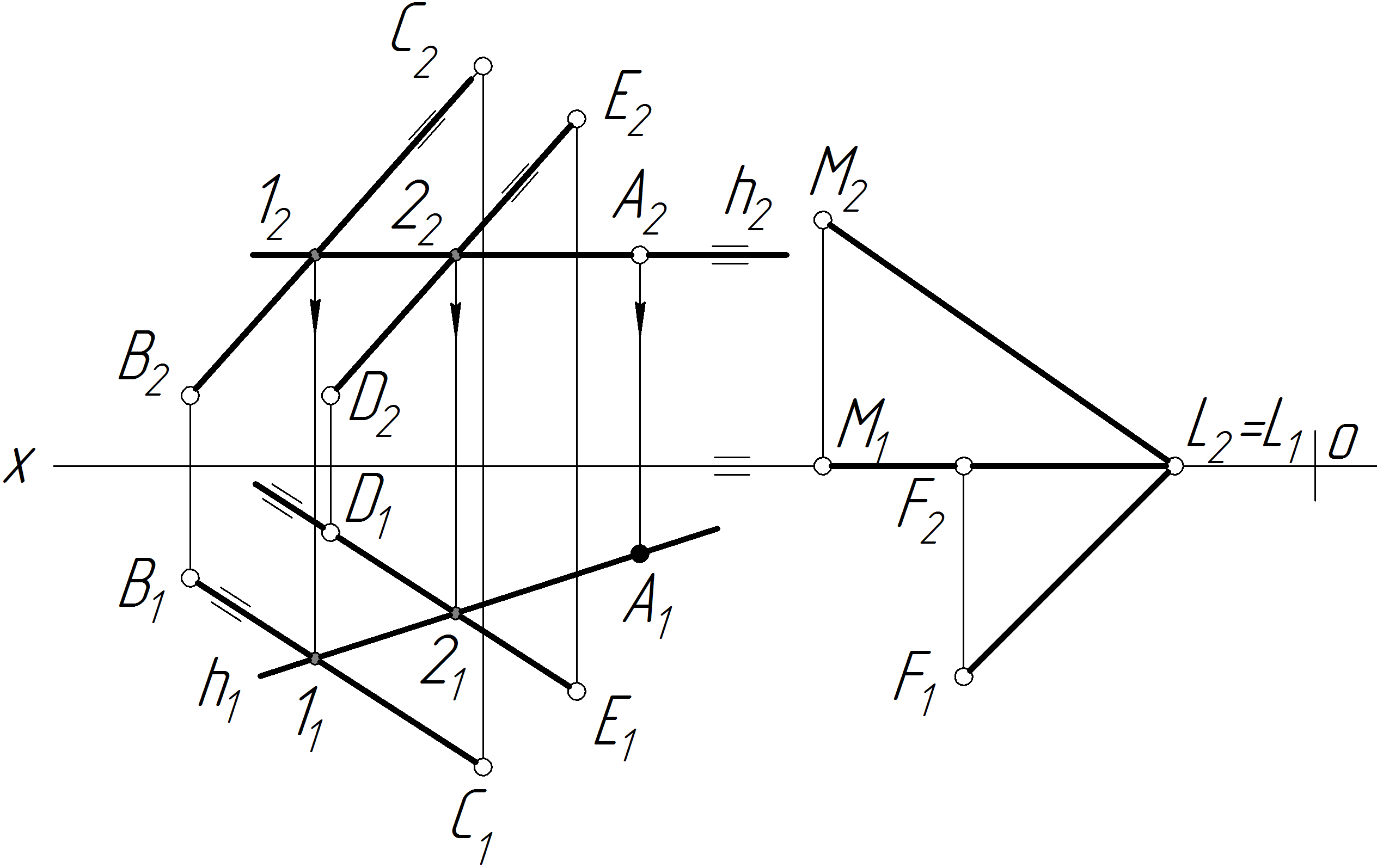
2. Побудувати площину через точку А паралельно до площини  (LMLN):

а) побудувати горизонталь (фронталь) через точку А шуканої площини;

б) побудувати сліди шуканої площини  (₂ ,₁ ), яка паралельна до площини  (LMLN).

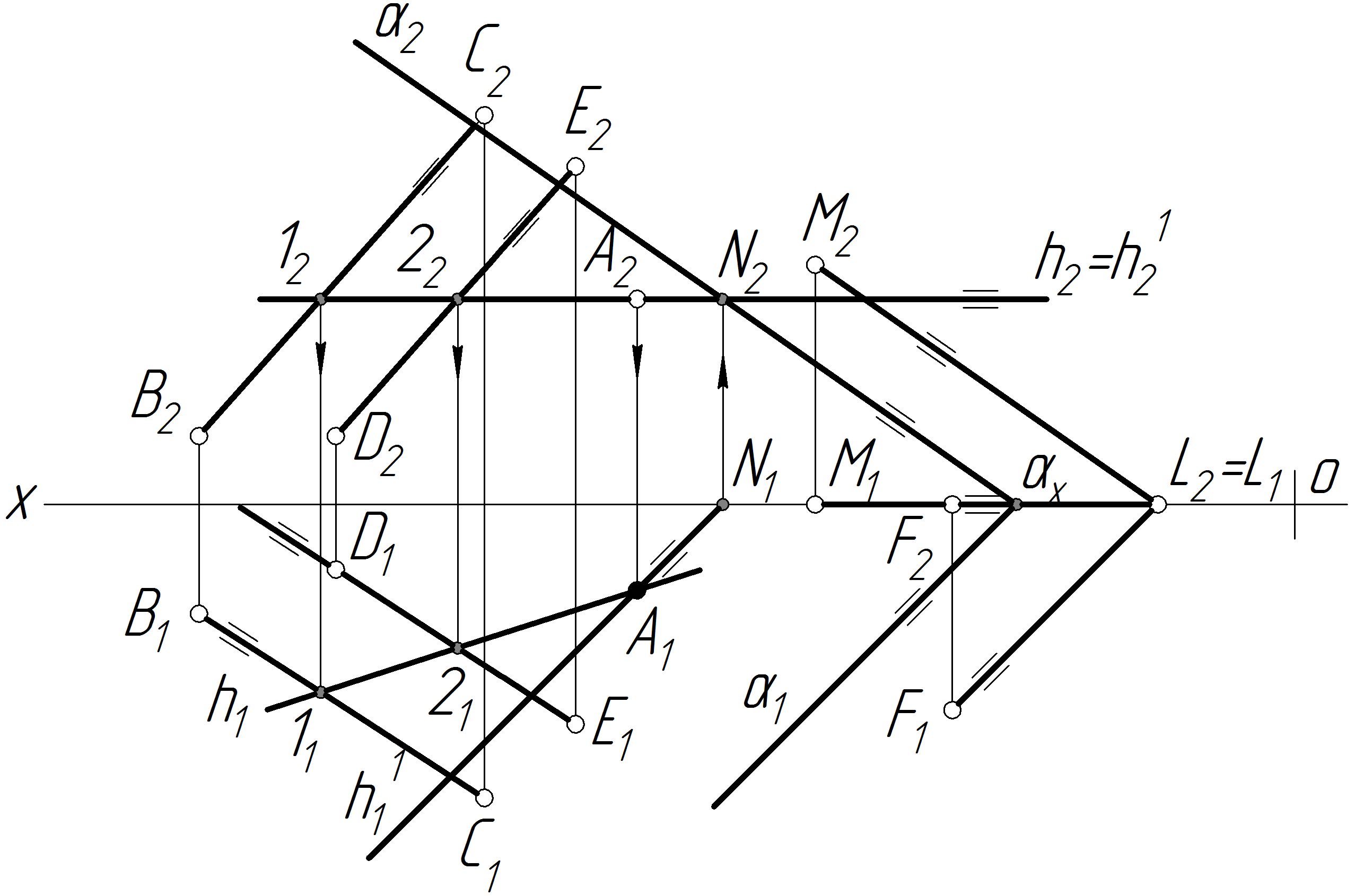
3. Знайти точку перетину прямої з площиною:

а) заключити відрізок DE (або ВС) площини Q у проекційну площину  ;

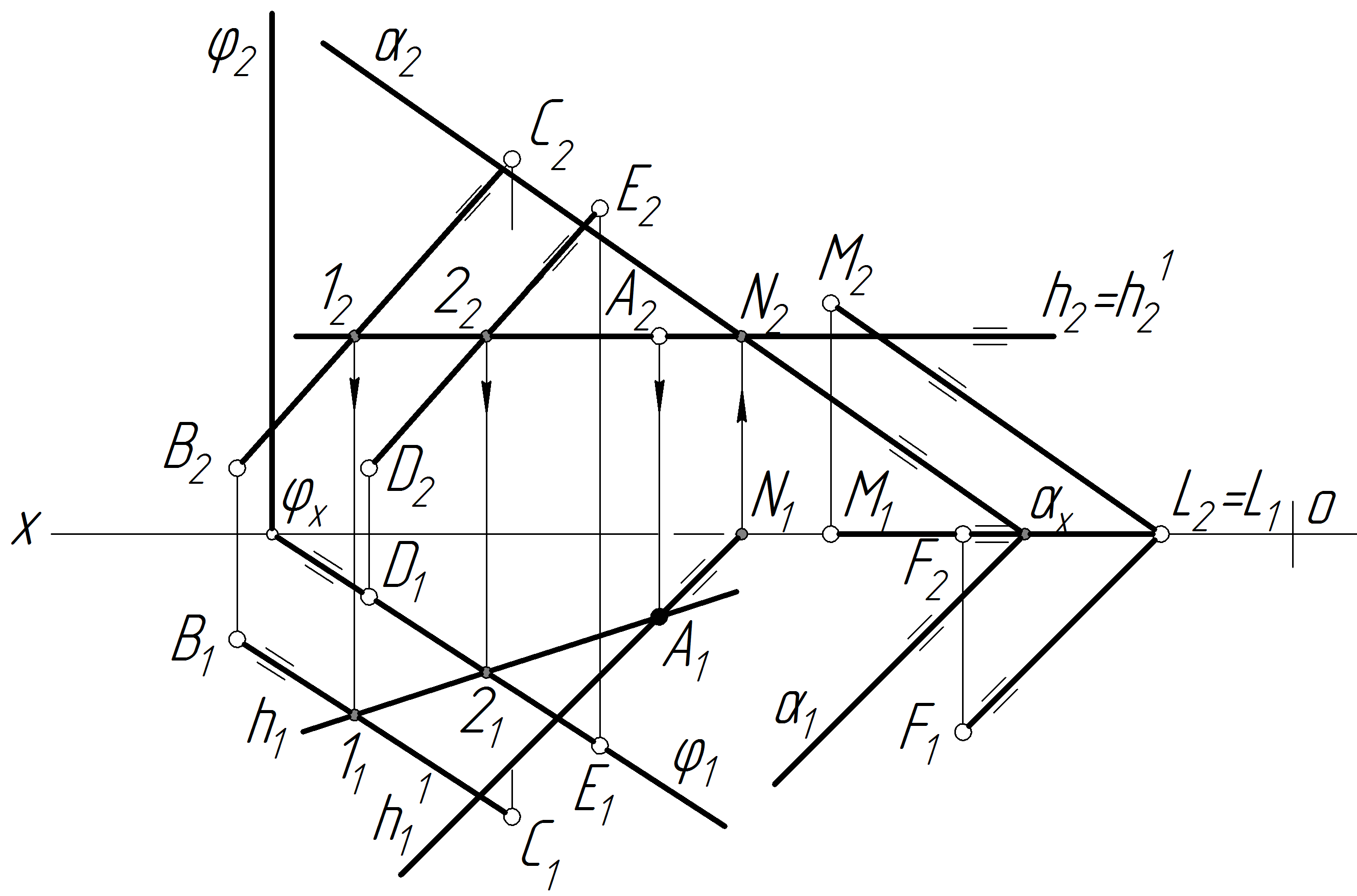
б) побудувати лінію перетину двох площин  і  — 34(3₂ 4₂ ;3₁ 4₁ );

в) знайти точку перетину прямої , яка задана відрізком DE (або ВС) з площиною  — точку К (К₂ К₁ ).

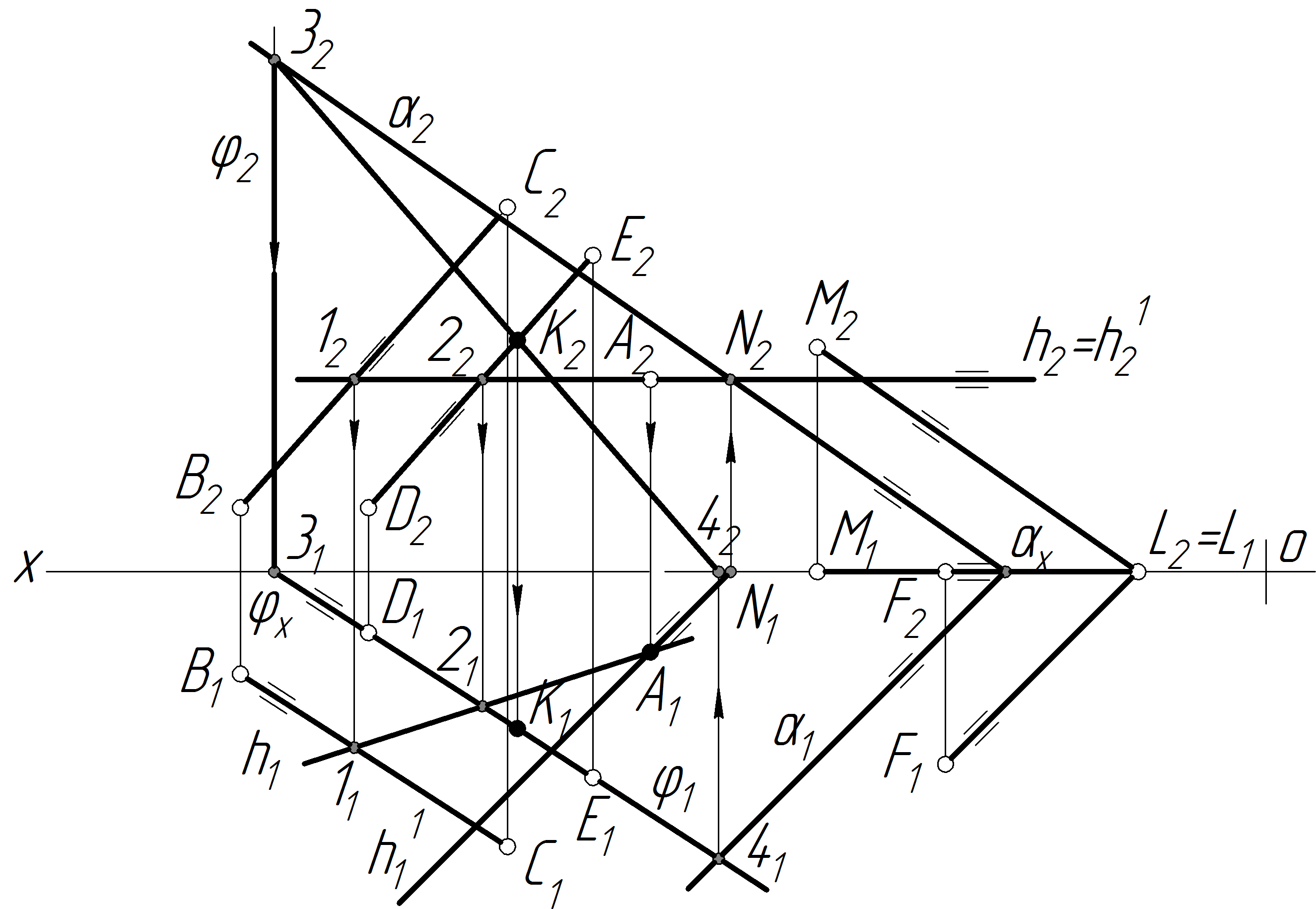
4. Побудувати АК (А₂ К₂ , А₁ К₁ ) — пряму, яка проходить через точку А паралельно площині  .

Задача 18 Задано площину Q (LMLN) та площину  (АВС ). Побудувати у площині Q геометричне місце точок, яке рівновіддалене від площини  на l мм (дати один розв’язок).

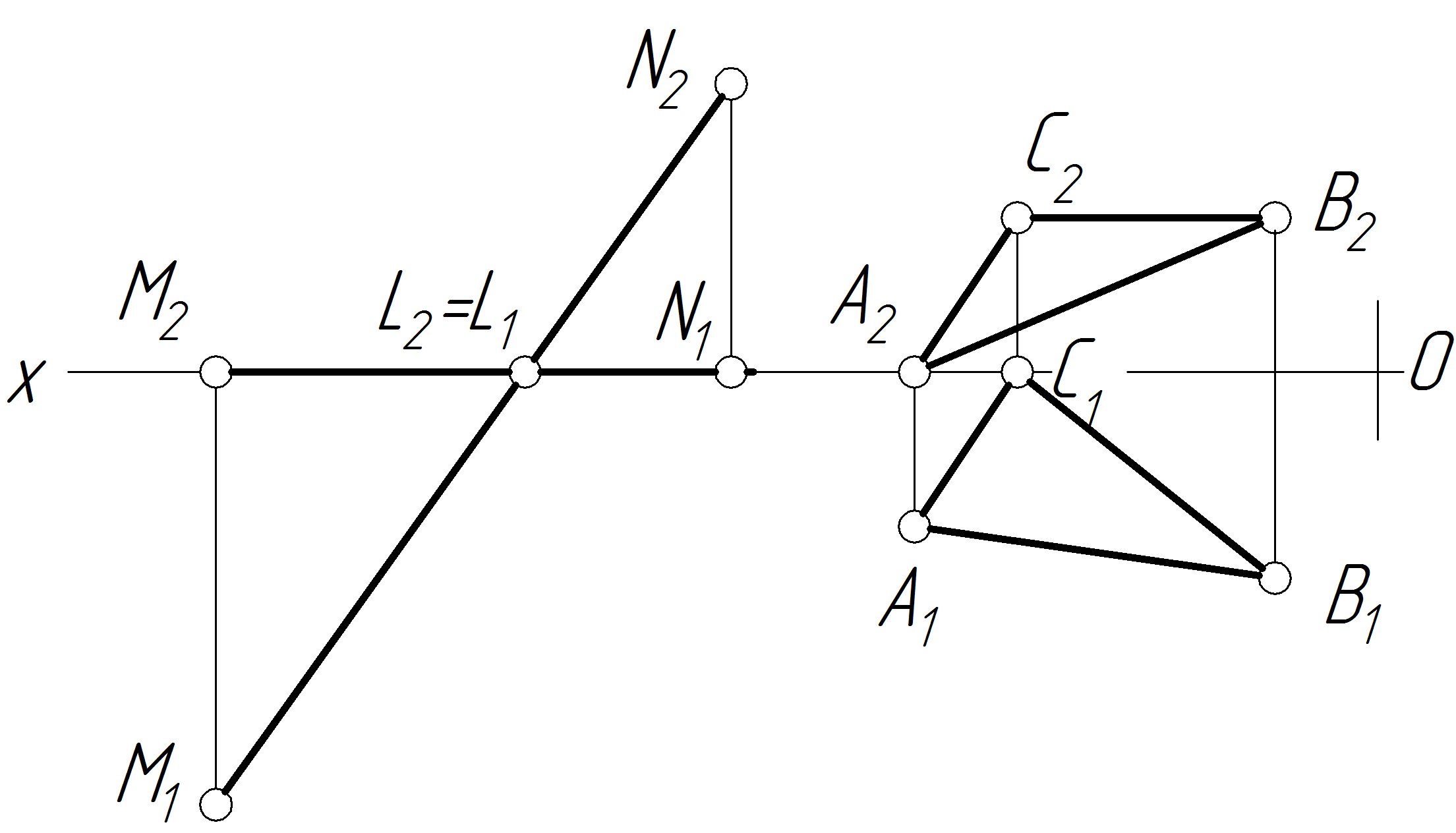
Рисунок 2.31 — Графічна умова задачі

План розв'язку

1. У площині  (АВС ) проводимо перпендикуляр через точку С до АВС

2. Обмежуємо перпендикуляр у довільній точці К і знаходимо дійсну величину відрізка СК за правилом прямокутного трикутника.

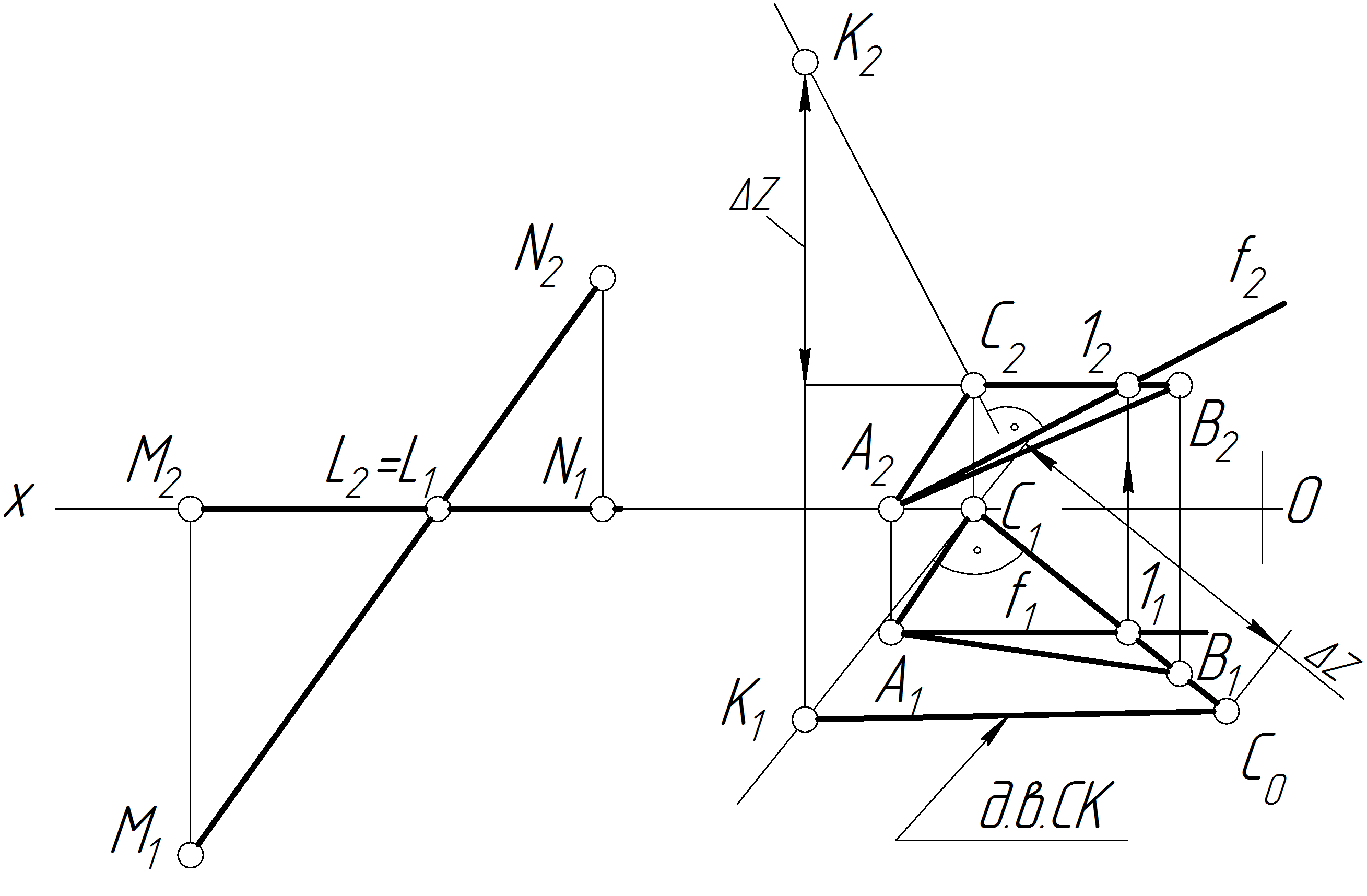
3. На відрізку СК знаходимо точку Е, яка знаходиться на відстані l від АВС

4. Через точку Е будуємо площину , паралельну до трикутника АВС — геометричне місце точок, яке рівновіддалене від площини  на l мм

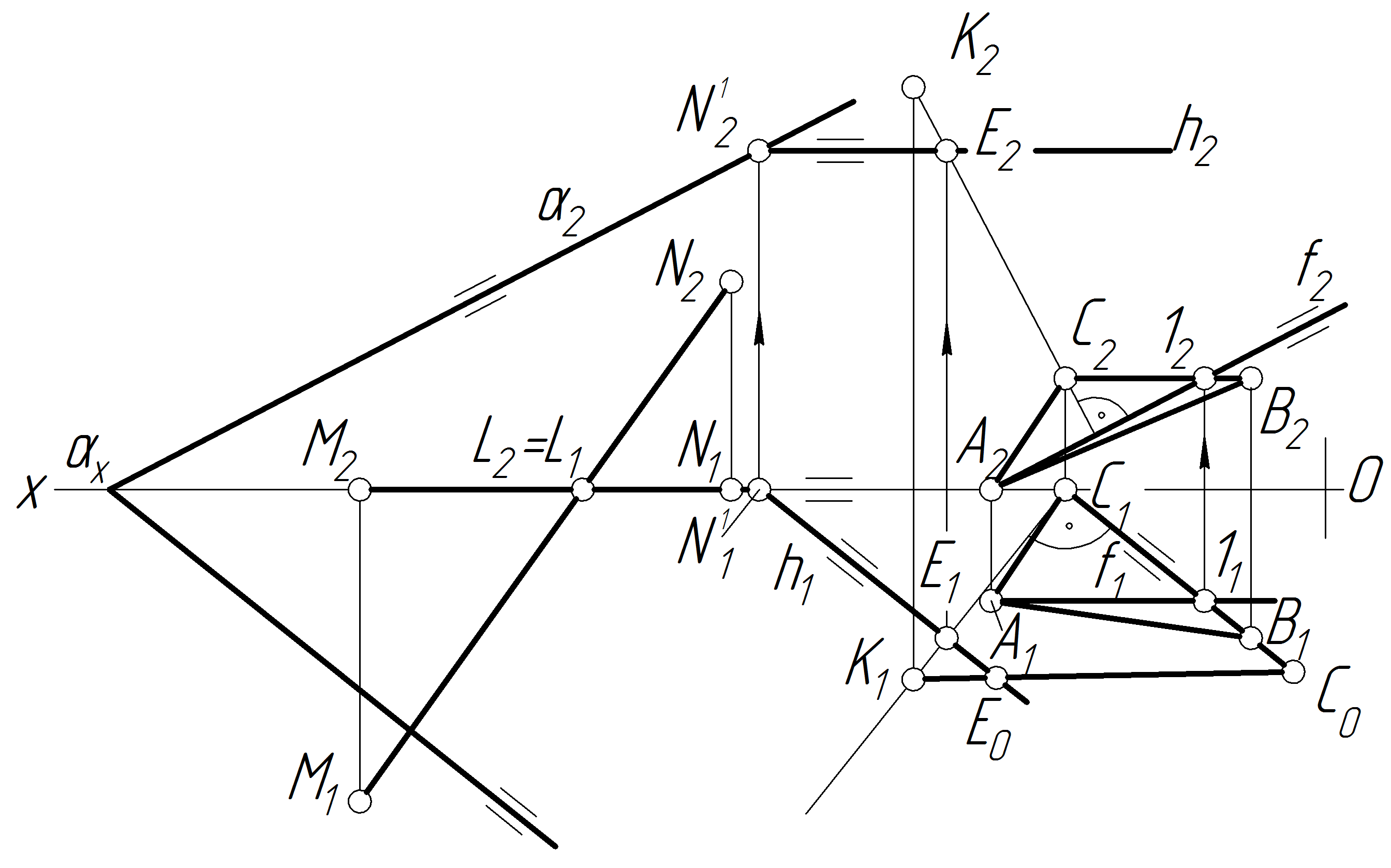
При розв’язуванні задач часто треба будувати проекції кута між прямою й площиною і кута між двома площинами. Зазначимо, що розв’язування таких задач повністю грунтується на наведених відомостях про взаємне положення двох площин, прямої й площини. Ці задачі можна розв’язати, користуючись викладеними вище міркуваннями і способами класичної нарисної геометрії, однак, для розв’язку цих задач можна використати способи, які будуть викладені в наступному розділі. За допомогою способів перетворення епюра розв’язок і побудова значно спрощується.