2.2 Взаємне положення прямої і площини

Пряма і площина можуть займати одна відносно іншої такі положення:

пряма належить площині; пряма паралельна площині; пряма перетинає площину.

П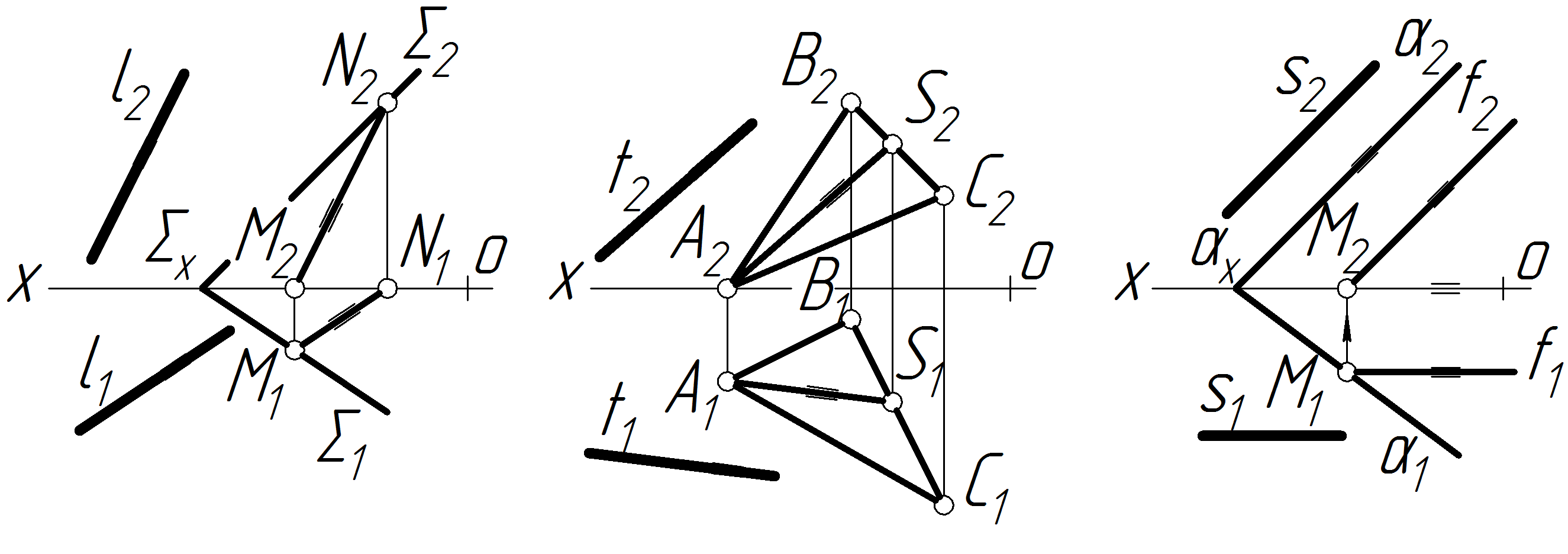 ряма паралельна до площини, коли вона паралельна будь-якій прямій, яка лежить у цій площині (рис. 2.15)

Рисунок 2.15 –Пряма, паралельна до площини

Пряма перетинає площину тоді, коли вона не належить площині і не паралельна їй, а перетинає її в певній точці. Якщо пряма загального положення перетинається з площиною особливого положення, то точка перетину знаходиться без додаткової побудови.

Н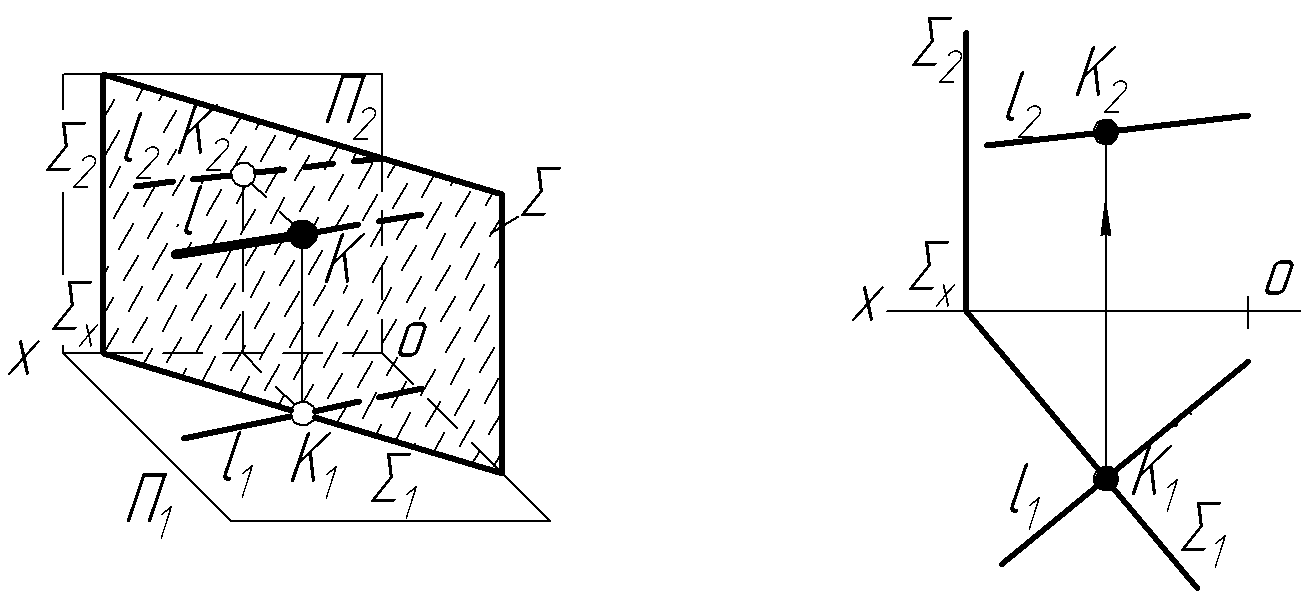 а рисунку 4.29 зображена пряма l і горизонтально-проекційна площина . Точка К належить і прямій l і площині . Горизонтальна проекція К₁ буде обов’язково лежати на горизонтальному сліді ₁ проекційної площини .

Рисунок 2.16 — Перетин прямої з площиню особливого положення

Для побудови точки перетину прямої з площиною загального положення треба виконати такі побудови (рис.2.17):

1. Через задану пряму ав провести допоміжну площину  (особливого положення);

2. Побудувати лінію перетину mn заданої площини  з допоміжною ;

3. Зробити висновок про положення прямих mn і ав.

Такий висновок необхідно зробити тому, що пряма MN спільна для площин  і , а пряма АВ лежить тільки в площині . Як результат зробленого аналізу можна виділити такі випадки:

а) прямі MN і АВ не мають спільних точок – пряма АВ паралельна до площини ;

б) прямі MN і АВ збігаються ─ пряма АВ лежить у площині ;

в) прямі MN і АВ перетинаються ─пряма АВ перетинає площину  в точці К.

На рисунку 2.17 задано площину  (довільного положення) і пряму АВ, яка перетинає цю площину. Через пряму АВ проводимо допоміжну горизонтально-проекційну площину ; лінія MN – це лінія перетину двох площин  і . Точка К, яка є точкою перетину прямих MN і АВ – шукана точка перетину прямої АВ з площиною  .

Розглянутий план розв’язку є загальним для всіх випадків задання площини.

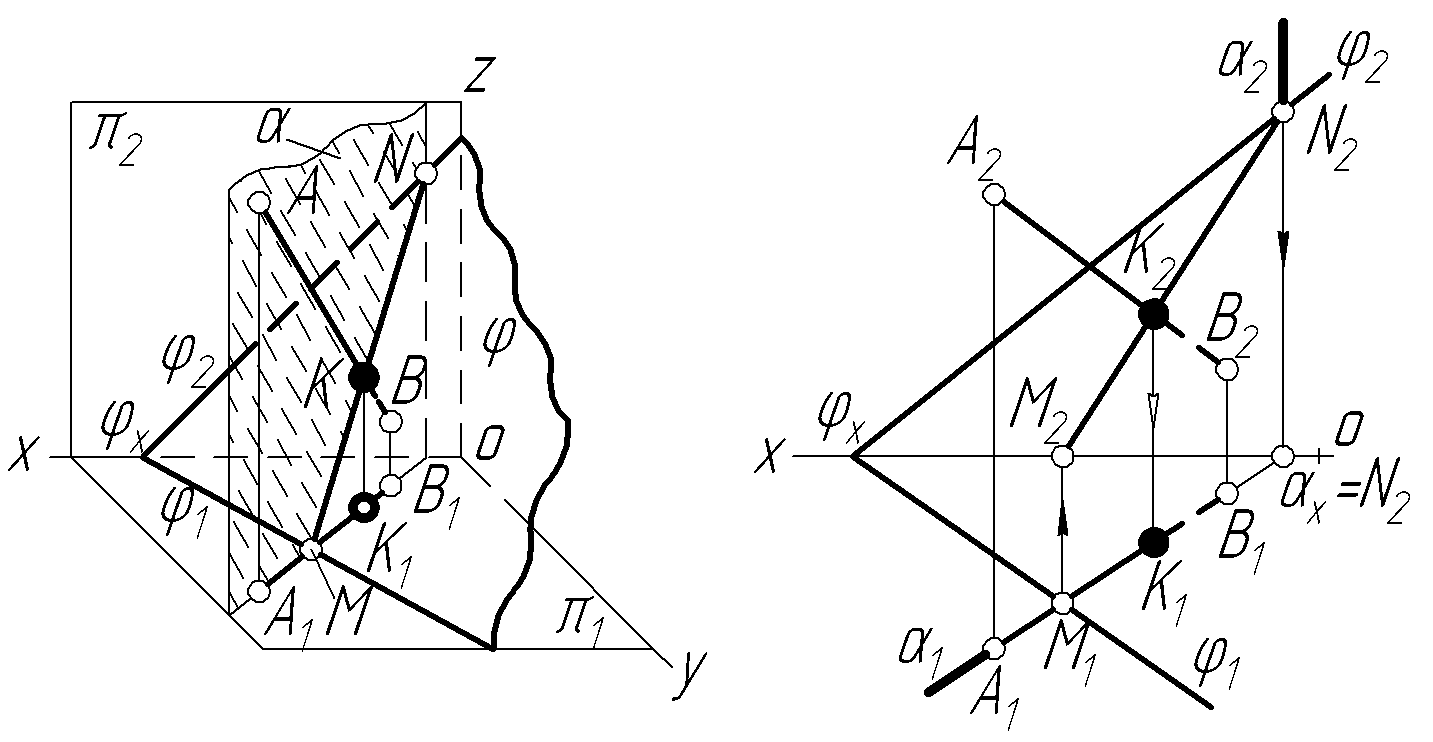
Рисунок 2.17 — Перетин прямої з площиною загального положення

Пряму перпендикулярну до площини слід розглядати як окремий випадок прямої, яка перетинає площину під прямим кутом.

З курсу елементарної геометрії відомо, що пряма перпендикулярна до площини, якщо вона перпендикулярна до двох перетинних прямих, які лежать у даній площині (рис.2.18,а).

Н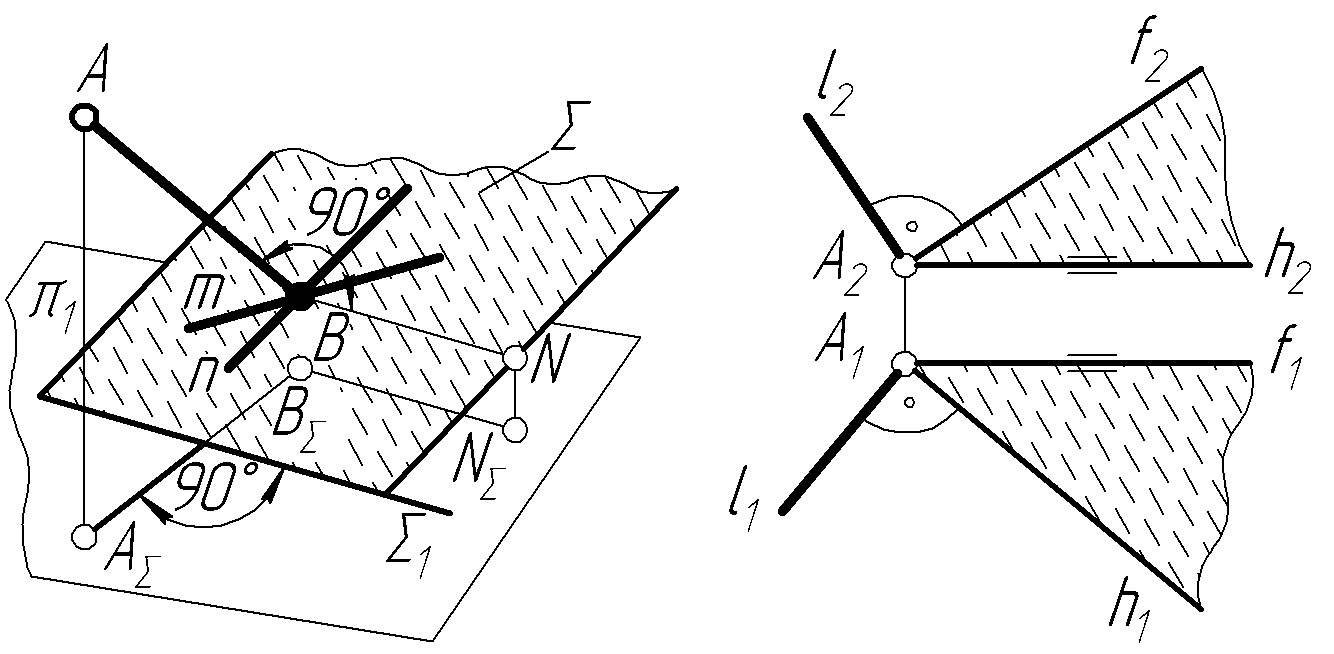 а комплексному рисунку горизонтальна проекція перпендикуляра до площини є перпендикулярною до горизонтального сліду площини, а фронтальна – до фронтального сліду площини.

а)

б)

Рисунок 2.18

На основі властивостей проектування прямого плоского кута можна зробити висновок, що проекції перпендикуляра до площини будуть розміщені таким чином: