Розділ 2 позиційні та метричні задачі. Способи перетворення проекцій

Позиційними називають задачі, пов’язані з розв’язуванням на епюрі питань взаємного розміщення геометричних фігур або їх елементів. До них належать задачі на взаємну належність і на взаємний перетин.

Метричними називають задачі, пов’язані з визначенням на епюрі дійсних величин відстаней, кутів і плоских фігур.

Метричні і позиційні задачі на епюрі розв’язуються значно легше, якщо задані геометричні фігури займають особливе положення відносно площин проекцій. Тому, щоб спростити розв’язування задач, часто доцільно вдатися до такого перетворення заданих проекцій на епюрі, яке дає змогу перевести геометричні елементи із загального положення до особливого. У результаті цього нові проекції дають змогу просто і зручно виявити форму елементів, взаємне положення та дійсні величини прямих, плоских фігур, кутів тощо.

Перетворення епюра відображає зміну положення геометричних образів або площин проекцій у просторі. В основному використовуються два способи перетворення проекцій: заміна площин проекцій та обертання.

2.1 Взаємне положення двох площин

Дві площини у просторі можуть бути паралельними або перетинними. У першому випадку вони не мають спільних точок, у другому спільними точками цих площин є лінія їх перетину.

Д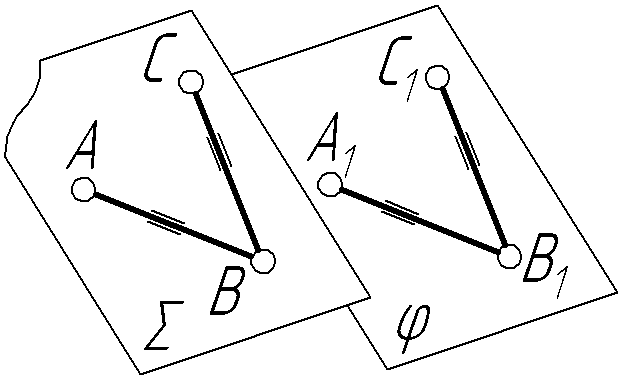 ві площини паралельні (рис. 2.1) тоді, коли дві перетинні прямі однієї площини відповідно паралельні двом перетинним прямим другої площини.

У площині  дві прямі АВ і ВС перетинаються і паралельні відповідно А₁В₁ і В₁С₁ двом перетинним прямим площини .

Рисунок 2.1 – Паралельні площини

У просторі

Якщо площини паралельні, то їх однойменні сліди також паралельні. Справедливим буде і обернене твердження .

Н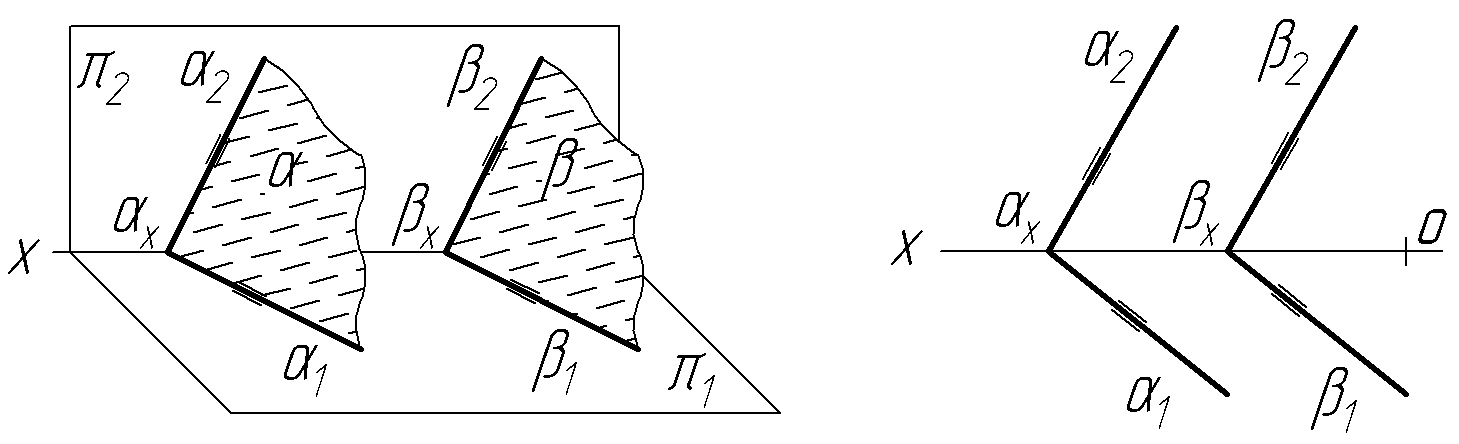 а рисунку 2.2 зображені дві паралельні площини  і , які задані слідами.

а) б)

Рисунок 2.2 –Взаємно паралельні площини:

А) на наочне зображення; б) епюр

Виходячи з того, що сліди площини є нульовими горизонталями, фронталями і профілями, справедливий також висновок: у паралельних площинах горизонталі, фронталі і профілі однієї площини паралельні відповідно до горизонталей, фронталей і профілей другої площини.

С

Рисунок 2.3 – Перетин двох площин

лід зауважити, що для площин довільного положення, заданих слідами, достатньо лише паралельності двох слідів на епюрі, щоб стверджувати – ці площини паралельні. Але, якщо це дві площини особливого положення (зокрема профільно-проектуючі), то судити про паралельність площин за двома парами слідів не можна (рис. 2.3). Обов’язково треба побудувати сліди площини на третій площині проекцій, до якої задані дві площини перпендикулярні, і тільки тоді можна стверджувати чи паралельні площини: якщо ₃║Δ₃ ─ то вони паралельні; якщо ₃Δ₃ ─ то вони перетинаються.

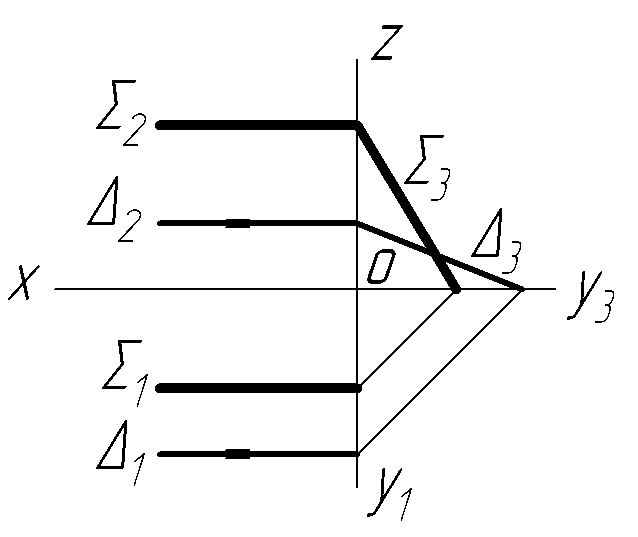
Отже, якщо хоч одна пара однойменних слідів двох площин перетинається, то такі площини перетинаються.

Д ві перетинні площини (рис. 2.4) перетинаються по прямій лінії, для побудови якої досить визначити дві точки, що одночасно належать обом площинам, або одну таку точку і напрямок прямої перетину (рис.2.5).

а) б)

Р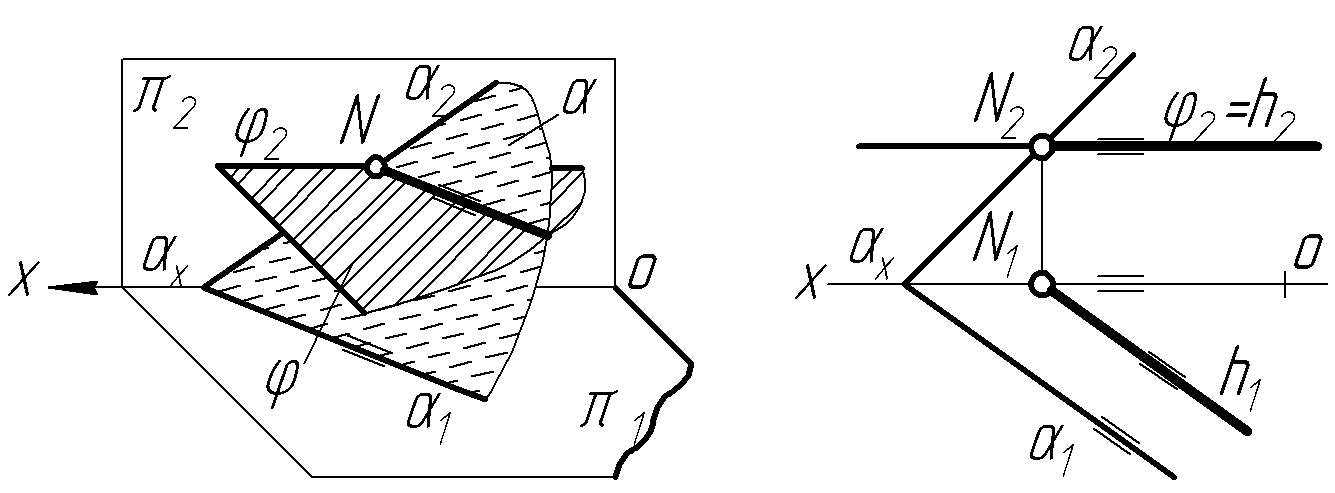 исунок 2.4 ─ Перетин площин,заданих слідами: а) наочне зображення; б)епюр

а) б)

Рисунок 2.5 — перетин площин, у яких одна пара слідів паралельна:

а) наочне зображення; б)епюр

Г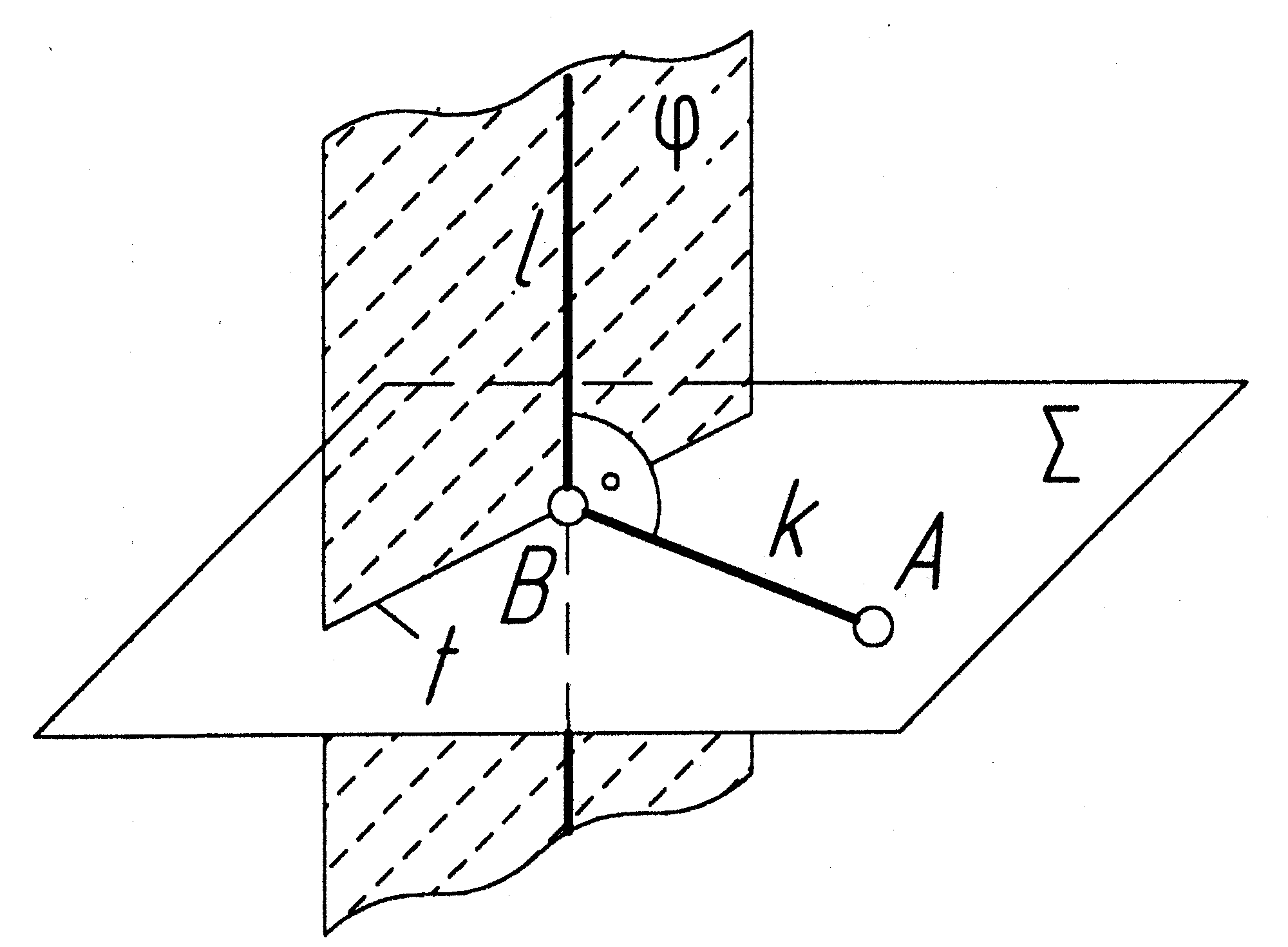 оризонтальна площина з будь-якою іншою площиною перетинається по спільній горизонталі, а фронтальна ─ по спільній фронталі.

Взаємно перпендикулярні площини – це окремий випадок двох площин, які перетинаються під прямим кутом. Дві площини взаємно перпендикулярні тоді, коли:

одна площина проведена через перпендикуляр до іншої;

Рисунок 2.6 — Взаємно

перпендикулярні площини

одна перпендикулярна до будь-якої прямої, що лежить у другій площині

Якщо йдеться про зображення на епюрі двох взаємно перпендикулярних площин, слід мати на увазі, що:

• о 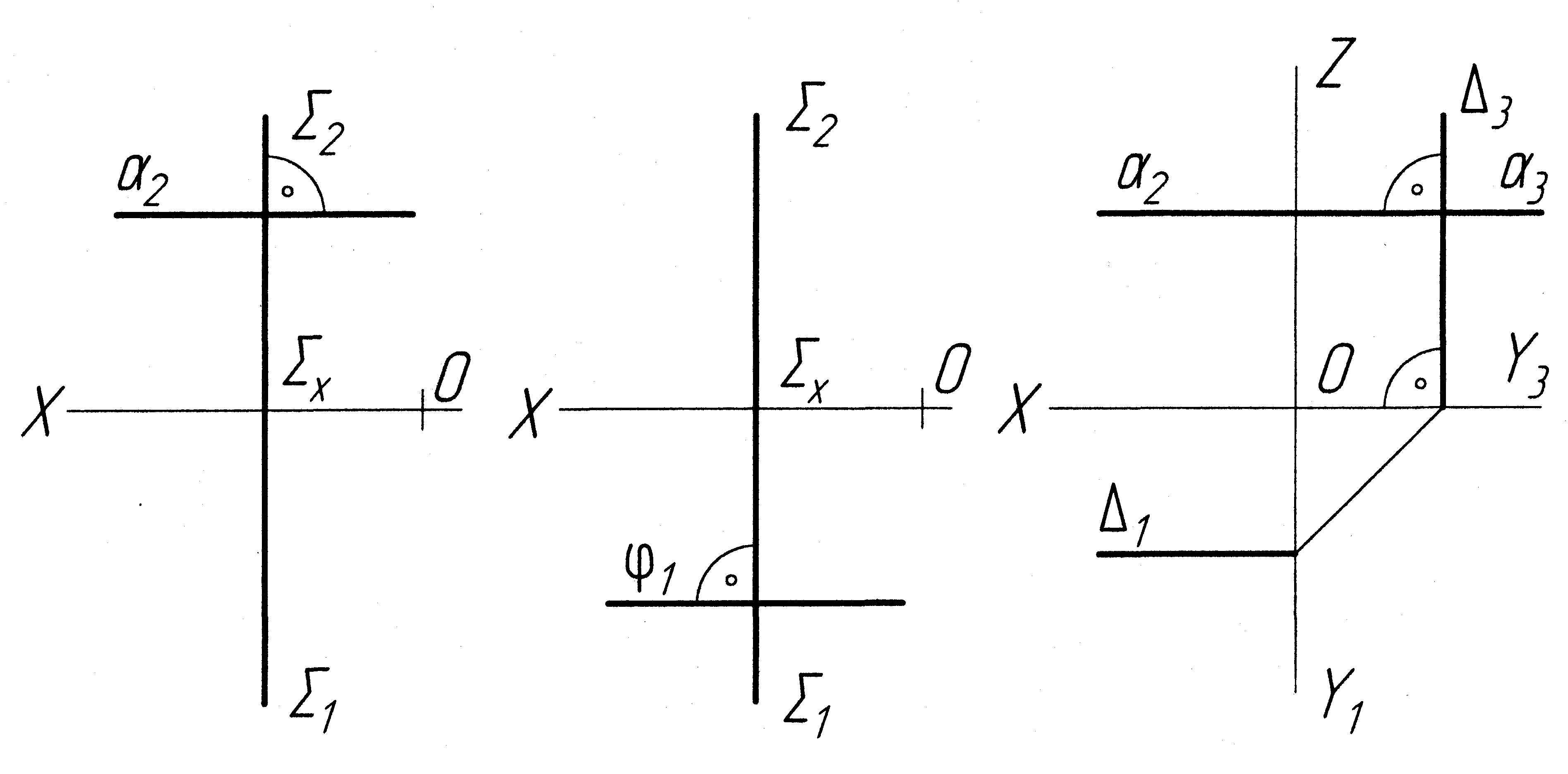днойменні сліди двічі проекційних площин взаємно перпендикулярні на тій площині проекцій, до якої обидві задані площини перпендикулярні (рис. 2.7);

а) б) в)

Рисунок 2.7 ─ Двічі проекційні площини перпендикулярні

• о 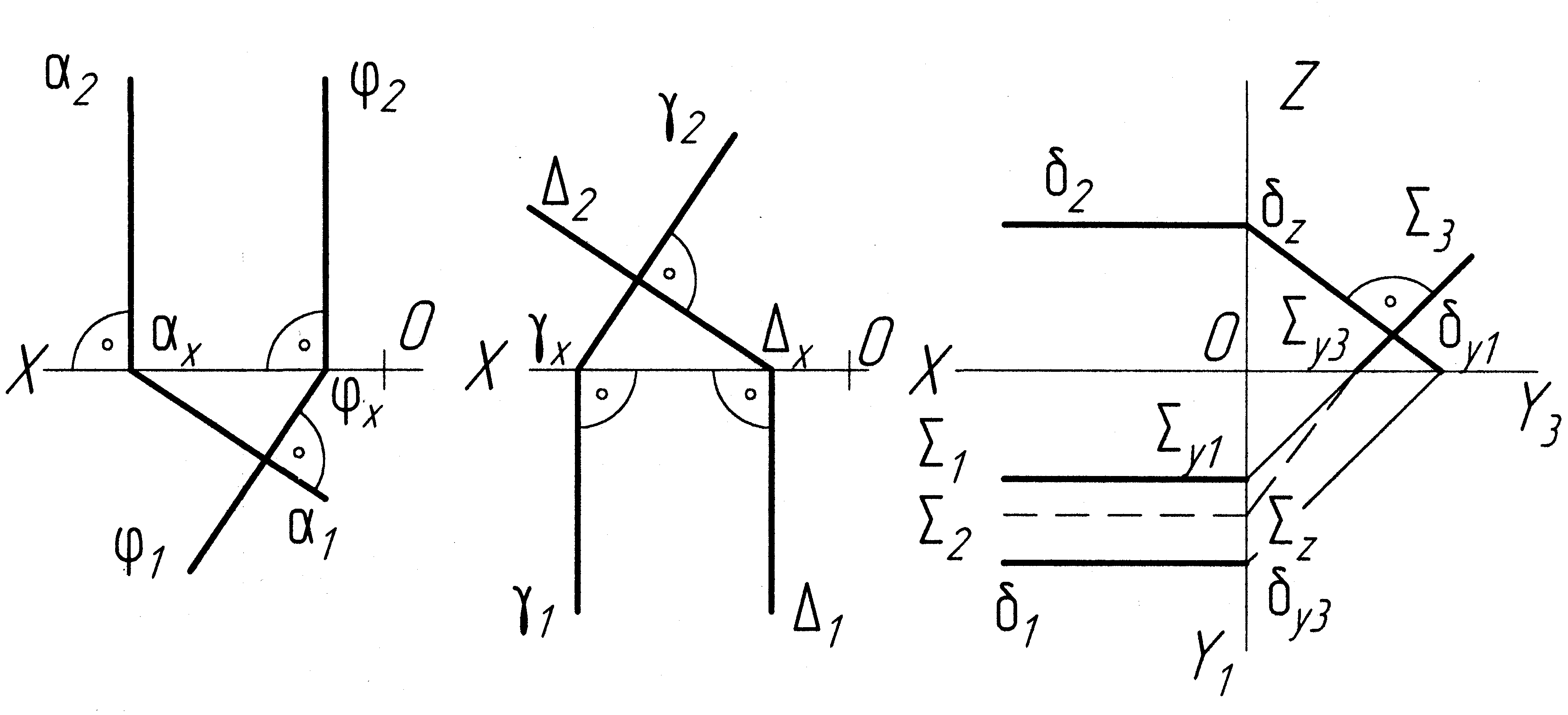днойменні сліди проекційних площин взаємно перпендикулярні лише на тій площині проекцій, до якої обидві задані площини перпендикулярні, інші сліди – ні (рис. 2.8);

а) б) в)

Рисунок 2.8 ─ Проекційні площини взаємно перпендикулярні

• якщо дві площини довільного положення на епюрі мають однойменні сліди перпендикулярні, то це не є ознакою перпендикулярності цих площин.

приклади розв’язку задач

Задача 1 Побудувати через точку А площину, паралельну до площини  (задати слідами) (рис. 2.9).

Ч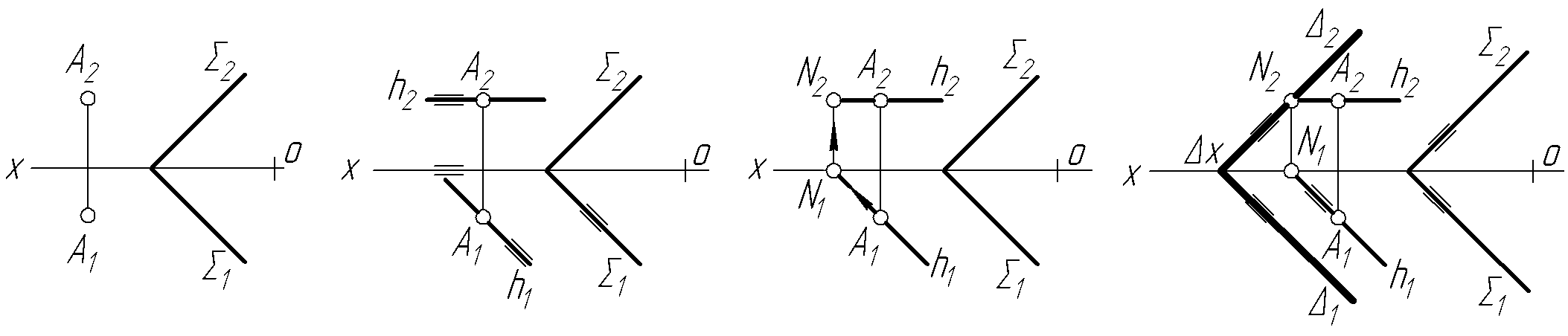 ерез точку А проводимо горизонталь площини Δ (яку треба побудувати). h₂║ОХ, а h₁║₁. Знаходимо фронтальний слід побудованої горизонталі N (N₂;N₁). Через фронтальний слід горизонталі NN₂ проводимо фронтальний слід Δ₂ площини Δ. Δ₂║₂ через N₂. Знаходимо точку сходу слідів Δ_Х . Δ₂ ОХ= Δ_Х. Будуємо горизонтальний слід площини Δ. Δ₁║₁. Отже, площини Δ і  — паралельні, оскільки їхні однойменні сліди паралельні і площина D проходить через точку А..

а) б) в) г)

Рисунок 2.9

Задача 2 Через точку D(D₁;D₂) провести площину D паралельно до площини трикутника АВС (рис. 2.10).

Побудова щуканої площини D зводиться до проведення через задану точку D двох перетинних прямих t і k відповідно паралельно до будь-яких двох сторін трикутника АВС, наприклад t || АС і k || ВС.

Д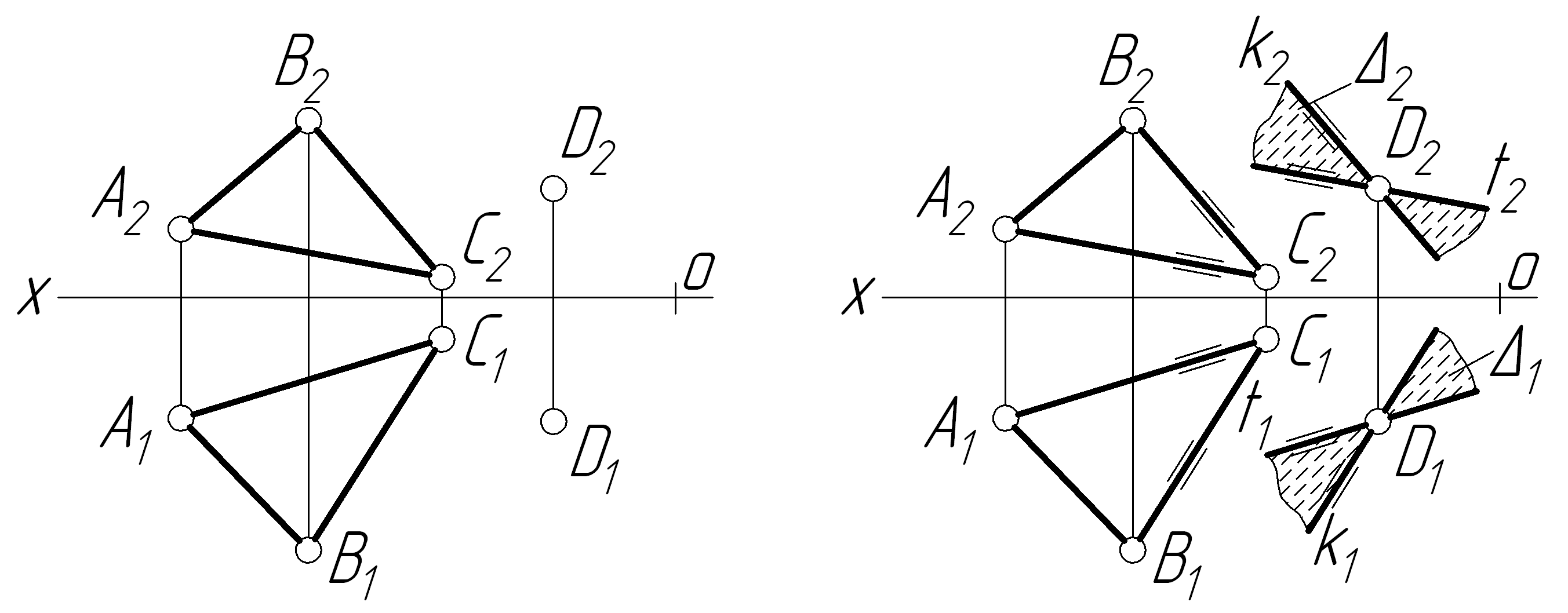 ві перетинні прямі t і k утворюють площину D, паралельну до площини трикутника АВС.

а) б)

Рисунок 2.10

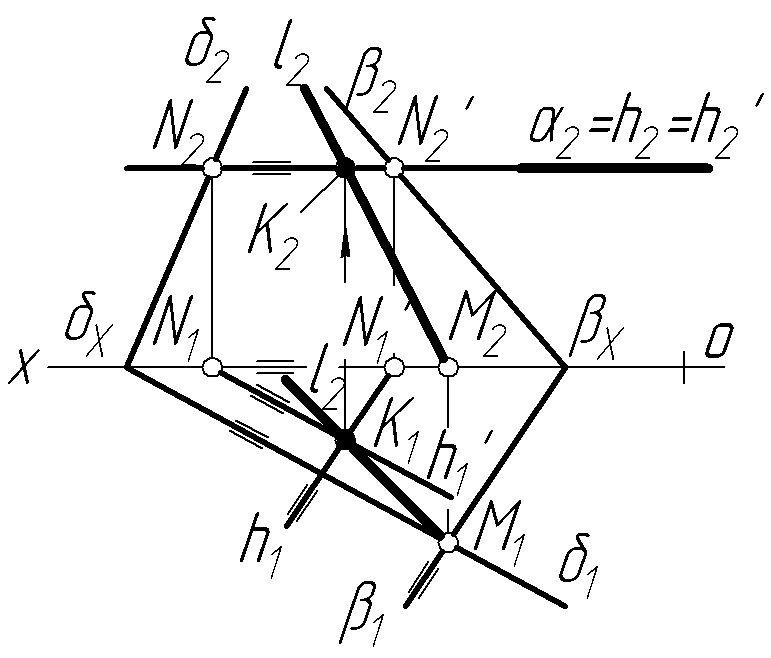
Задача 3 Побудувати лінію перетину двох площин  і  (рис.2.11).

У

Рисунок 2.11

даній задачі легко знаходиться одна точка лінії перетину. Вона лежить на перетині горизонтальних слідів площини М(М₁;М₂). Друга пара слідів перетинається за межами формату, тому треба знайти напрямок лінії перетину, тобто знайти іншу, довільну точку прямої перетину, спільну для обох площин. Скористаємося методом допоміжних січних площин-посередників. Обираємо площину-посередник розташовану в просторі так, щоб ця допоміжна площина перетинала обидві задані площини по лініях, які легко будуються — горизонталях або фронталях.

У даному випадку вибираємо горизонтальну площину , яка перетинає задані площини  і  по горизонталях h(h₂;h₁) та h( h₂; h₁). На перетині цих горизонталей дістанемо спільну для заданих площин допоміжну точку К(К₁;К₂) — h₁ і h₁ перетинаються в К₁. На лінії проекційного зв’язку на h₂₌h₂ знаходимо К₂.

З’єднавши К₂ з М₂ і К₁ з М_1, знайдемо шукану лінію перетину двох площин  і .

Задача 4 Побудувати площину Σ, перпендикулярну до заданої площини Δ (рис.2.12).

Б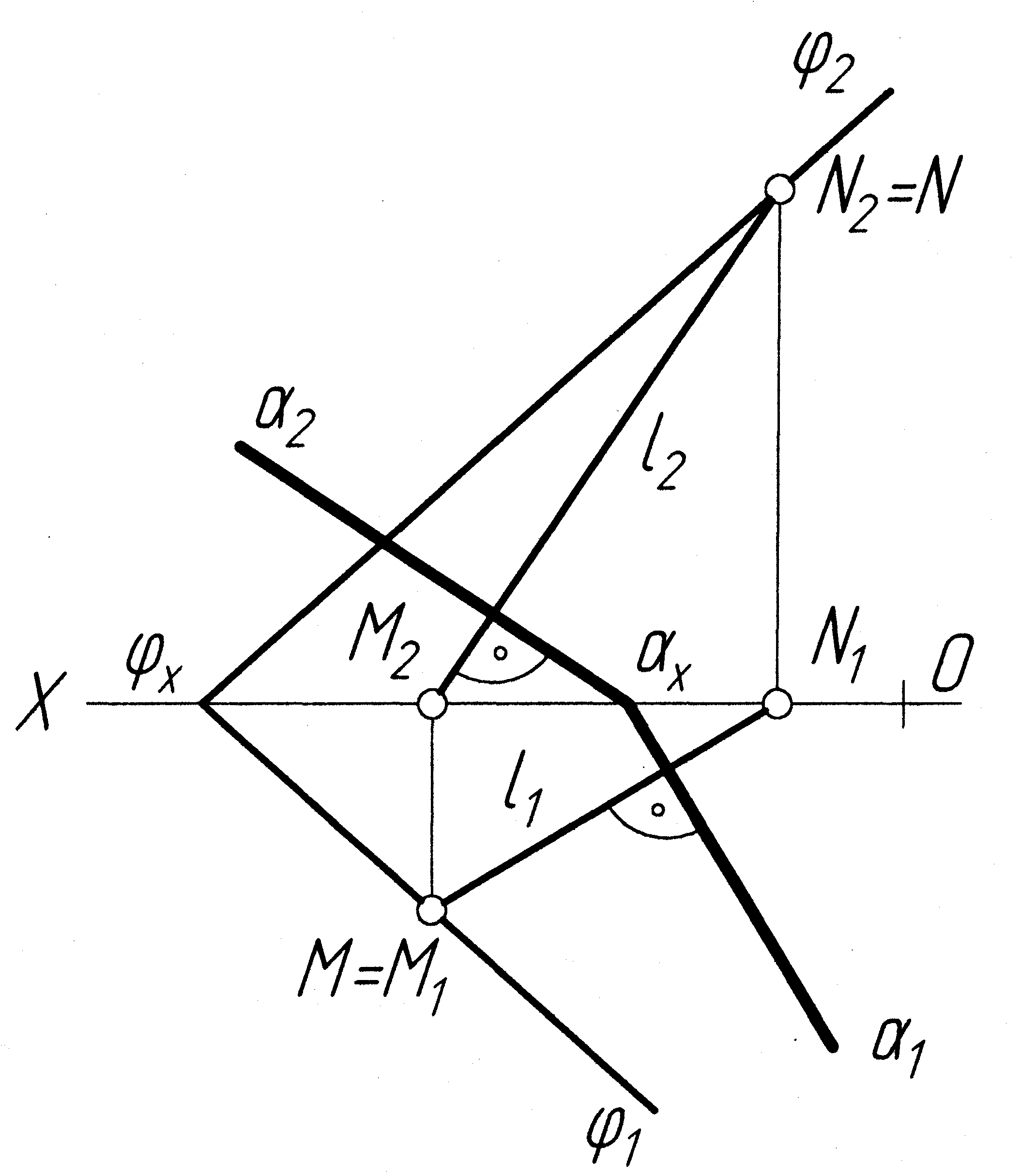 удуємо перпендикуляр l до площини Δ. Для цього проводимо l₁Δ₁ і l₂Δ₂ Через перпендикуляр l проводимо площину Σ (у даному випадку горизонтально-проекційну). Оскільки через перпендикуляр l можна провести безліч площин, то шукана площина Σ є однією з них.

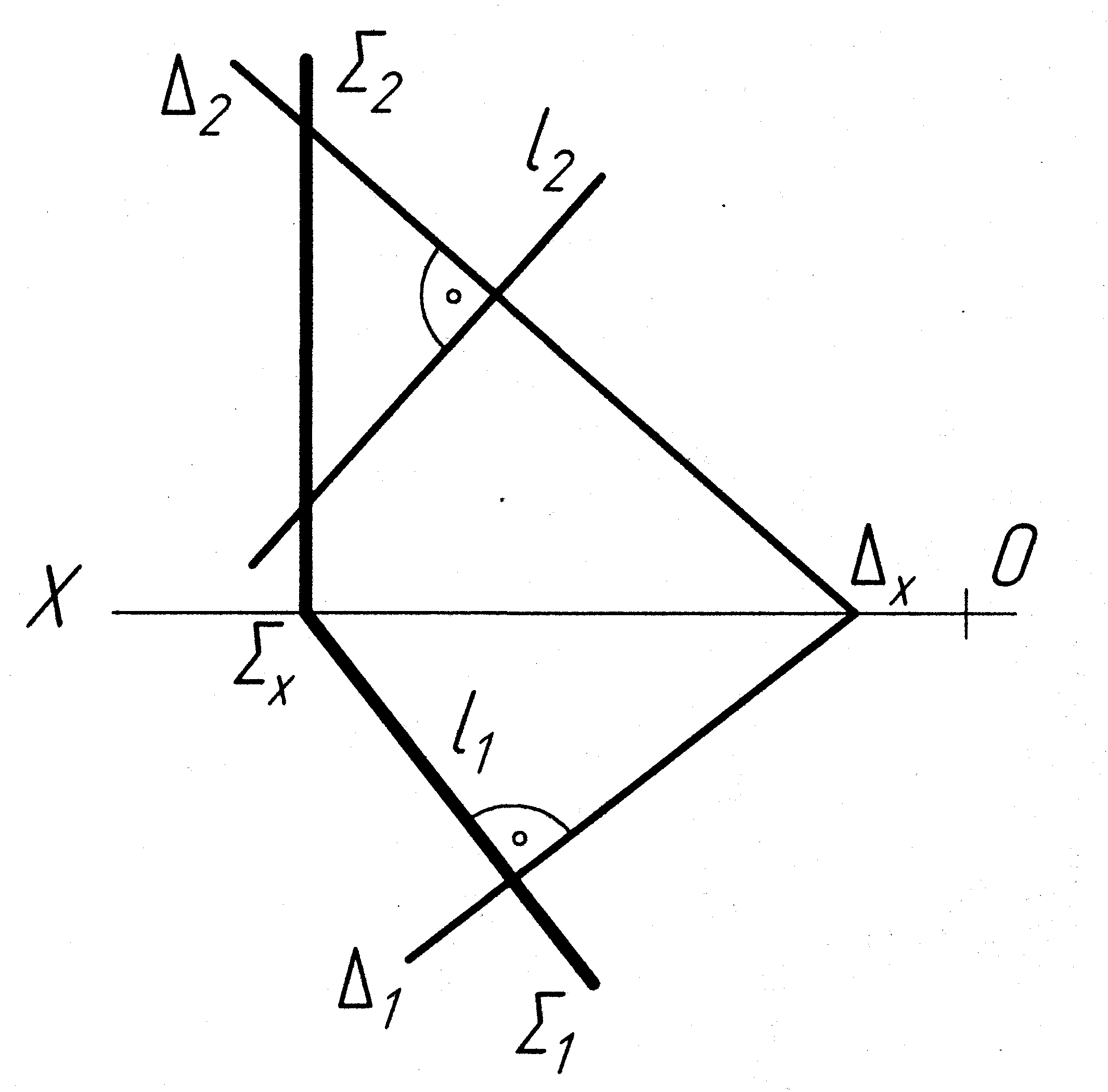
Рисунок 2.12

Рисунок 2.13

Задача 5 Побудувати площину , перпендикулярну до площини  (рис.2.13).

У заданій площині  будуємо довільну пряму l, перпендикулярно до якої проводимо площину  — одну із безлічі можливих. Площини  і  взаємно перпендикулярні. Наведені приклади підтверджують положення, що в обох випадках задачі мають безліч розв’язків. Тому, щоб дістати єдиний розв’язок, потрібна додаткова умова.

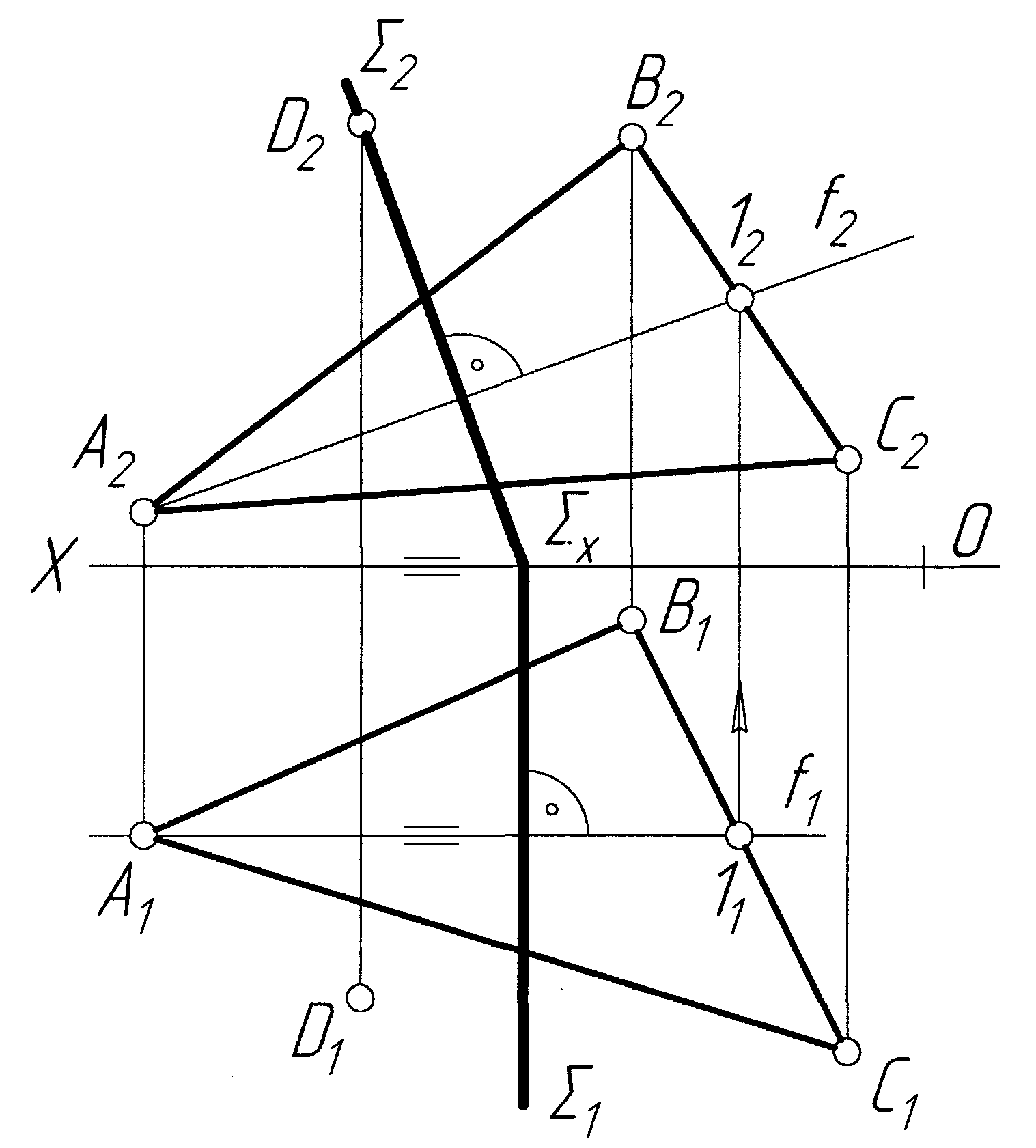
Задача 6 Через задану точку D провести фронтально-проекційну площину , перпендикулярно до площини трикутника АВС (рис.2.14).

Д

Рисунок 2.14

одатковою умовою в цій задачі є перпендикулярність шуканої площини до площини трикутника АВС і фронтальної площини проекцій. Тому спочатку у заданій площині проводимо фронталь f(f₁;f₂), до якої будуємо перпендикулярну площину : ₂f₂ i, очевидно, ₁f₁. Таким чином, площина  перпендикулярна до заданої, бо вона перпендикулярна до однієї з її фронталей, і проходить через точку D.