Продовження рисунка 7.37

7.7 Перетин поверхонь обертання площиною загального положення

Для визначення лінії перерізу поверхонь обертання площиною довільного положення необхідно ввести ряд допоміжних площин певного положення, які у перетині з поверхнею утворюють найпростіші фігури – коло, прямі лінії, а у перетині січною площиною – прямі. Це, звичайно, не є складний, але трудомісткий процес, тому доцільніше скористатися методом заміни площин проекції (розділ 5), що є найбільш раціональним у даному разі методом перетворення проекції.

Задача. Визначити проекції та дійсну величину перерізу конуса площиною довільного положення (рис.7.38).

С користаємося заміною площин проекції і перетворимо площину загального положення у фронтально-проекційну площину. Для цього нову вісь проекції Х₁₄ проведемо перпендикулярно до , виберемо довільну точку N₂ на фронтальному сліді заданої площини  і побудуємо її положення в системі ₁-₄ - це буде точка N₄, новий слід ₄ уже проекційної площини пройде через _х4 і точку N₄ так само заміною площин проекції побудуємо нову проекцію конуса в системі ₁-₄.

Рисунок 7.38

Тепер задача зводиться до перетину конуса проекційною площиною, який описаний в підрозділі 7.4.

Лінією перетину конуса площиною  в даному випадку буде еліпс (площина  перетинає всі твірні конуса). Проекціями цього еліпса на площинах проекцій на ₂₁ будуть також еліпси, але інших розмірів (рис.7.38).

Еліпс легко будується, коли знаємо його осі, тому перш за все треба визначити осі еліпса та його проекцій.

Велика вісь еліпса дорівнює відрізку 1₄2₄, який є проекцією еліпса на площину ₄. Розділивши цей відрізок навпіл, одержимо точку 3₄≡4₄, що і буде проекцією малої осі еліпса. Мала вісь еліпса розміщена перпендикулярно площині ₄.

Тепер можна знайти горизонтальні площини проекції 34 і 12 осей еліпса. При чому, відрізок 3₁4₁ буде дійсною величиною малої осі еліпса. Додаткові точки шуканої лінії перетину можуть бути знайдені як точки перетину твірних конуса з площиною .

Дійсна величина шуканого еліпса знайдена методом суміщення. При цьому варто знайти осі еліпса, за якими і будується сам еліпс.

7.8 Перетин кривих поверхонь прямою лінією

Задачі на перетин прямої лінії з поверхнею розв’язуються аналогічно задачам на перетин прямої лінії з площиною.

Загалом, можна рекомендувати такий порядок побудови точок перетину прямої лінії з кривою поверхнею:

1. через дану пряму проводять допоміжну площину, так щоб лінія перерізу її з поверхнею проеціювалась на якусь із площин проекції у вигляді прямих або кола;

2. будують фігуру перерізу даної поверхні з допоміжною площиною;

3. у результаті цих побудов на перетині заданої прямої з фігурою перерізу одержують шукані точки

П ри розв’язку даної задачі щоразу буде поставати питання про вибір допоміжної площини для одержання простішого розв’язку задачі. Це питання розглянемо нижче на конкретних задачах.

На рисунку 7.39 наведено приклад визначення точок перетину прямої з поверхнею прямого кругового циліндра. У даному випадку немає сенсу застосовувати допоміжні побудови, тому що поверхня циліндра є горизонтально-проекційна, горизонтальні проекції точок А та В і є шуканими точками. Вони лежать на горизонтальній проекції кола основи циліндра.

Н

Рисунок 7.39 - Перетин циліндра з прямою

а рисунку 7.40 показано побудову точок перетину прямої l з поверхнею похилого циліндра. Оскільки бічна поверхня заданого циліндра не є проекційною (як в попередньому випадку), а пряма l довільного положення, задача на пошук точок перетину дещо ускладнюється і може бути вирішена введенням допоміжної січної площини.

У даному випадку з усіх можливих положень січної площини, проведеної через пряму l, вибираємо таку, яка в перерізі з циліндром утворить найпростішу фігуру – чотирикутник. Ця площина паралельна до осі циліндра. Площини іншого положення перетнуть циліндр по еліпсах, побудова яких складніша, аніж чотирикутника.

Вибір потрібної січної площини робимо таким чином. Позначаємо на прямій довільну точку S, через яку проводимо допоміжну пряму t паралельно до осі циліндра.

Пересічні прямі l і t утворюють площину , яка, будучи паралельною до осі циліндра, перетне його бічну поверхню по твірних, а циліндр – по чотирикутнику. Для побудови чотирикутника треба визначити горизонтальний слід ₁ площини , який проходить через горизонтальні сліди М₁ і М₁^* прямих l i t. Слід ₁ перетинає горизонтальну проекцію основи циліндра в точках 1 і 2, через які проводимо горизонтальні проекції твірних, за якими січна площина  перерізає бічну поверхню циліндра. Будуємо чотирикутник 1₁2₁3₁4₁, на перетині горизонтальної проекції прямої з цим чотирикутником знайдемо точки К₁ і S₁ – горизонтальні проекції шуканих точок перерізу, за ними - фронтальні проекції А₂ і S₂ на перетині відповідних ліній зв’язку з l₂ (показано стрілками).

Видимість прямої l на проекціях визначається за видимістю твірних – сторін фігури перерізу.

Н а рисунку 7.41 показано, як знайти точки “входу” і “виходу” горизонтальної прямої з конусом. У даному випадку через задану пряму треба провести горизонтальну площину , яка перетне конус по колу. У перетині цього кола із заданою прямою знайдемо шукані точки перетину прямої з поверхнею конуса.

Рисунок 7.40 ― Перетин прямої загального положення з похилим циліндром

Рисунок 7.41 ― Перетин прямої особливого положення з конусом

При перетині прямої лінії довільного положення з поверхнею конуса раціональним є скористатися площиною, яка проходить через вершину конуса і задану пряму. Така площина перетне поверхню конуса двома твірними (рис.7.42).

На прямій візьмемо довільні точки А і В і з’єднаємо їх з вершиною S. Знайдемо горизонтальні сліди прямих SА і SВ, через які проведемо горизонтальний слід ₁ допоміжної площини. Слід ₁ і горизонтальна проекція основи кола конуса перетинаються в точках C i D, тому що лежать в одній площині ₁. Побудуємо твірні конуса SC i SD, якими конус перетинається з допоміжною площиною. Точки 1 і 2 перетину твірних SC і SD з прямою АВ і є шуканими точками перетину заданої прямої з поверхнею конуса.

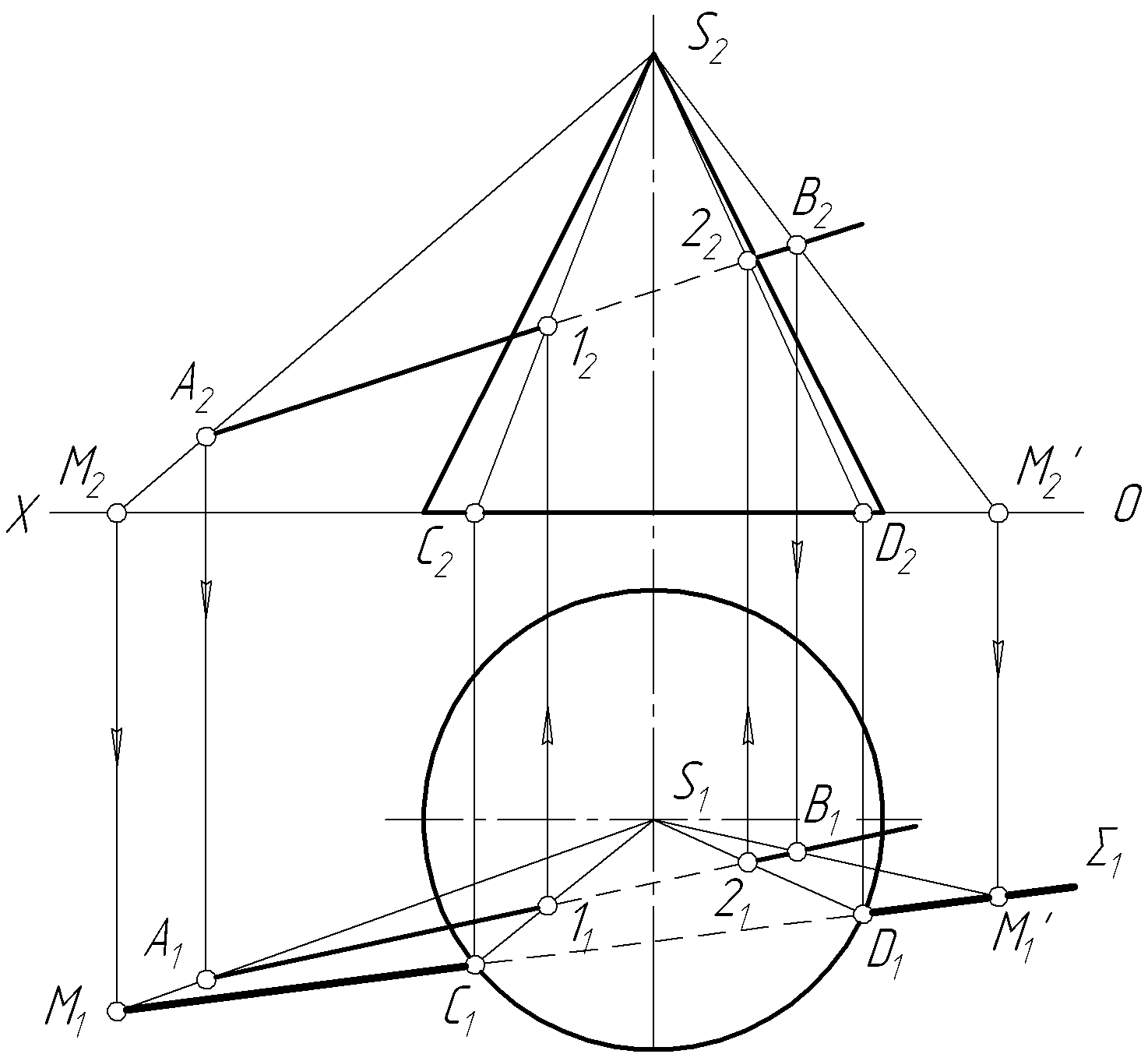
Рисунок 7.42 ― Перетин прямої загального положення з конусом

Задача. Визначимо точки перетину горизонтальної прямої із сферою (рис.7.43).

Вибрана тут допоміжна січна горизонтальна площина , проведена через пряму l, перетне сферу по колу. Перетин кола із заданою прямою на горизонтальній площині проекції дасть точки А₁ і В₁, за ними точки А₂ і В₂. Точки А і В – шукані. Видимість прямої визначаємо, виходячи із видимості точок на поверхні сфери.

На рисунку 7.44 побудовано точки 1 і 2, в яких пряма АВ перетинає поверхню сфери. У цьому випадку через пряму АВ проведена допоміжна площина , яка перпендикулярна до площини ₁ і перетинає сферу по колу. Задача розв’язана за допомогою способу заміни площин проекцій. Нова площина проекцій проведена паралельно площині  і в ній лежить пряма АВ і згадане вище коло. Коло проеціюється на нову площину проекцій ₄ без спотворення. Точками перетину кола з А₄В₄ будуть точки 1₄ і 2₄, які є шуканими. За ними будуємо проекції 1₁ і 2₁, а потім 1₂ і 2₂ (показано стрілками).

Рисунок 7.43 ― Перетин прямої особливого положення з кулею

Рисунок 7.44 ― Побудова перетину прямої з кулею методом заміни площин проекцій