7.3 Поверхні обертання

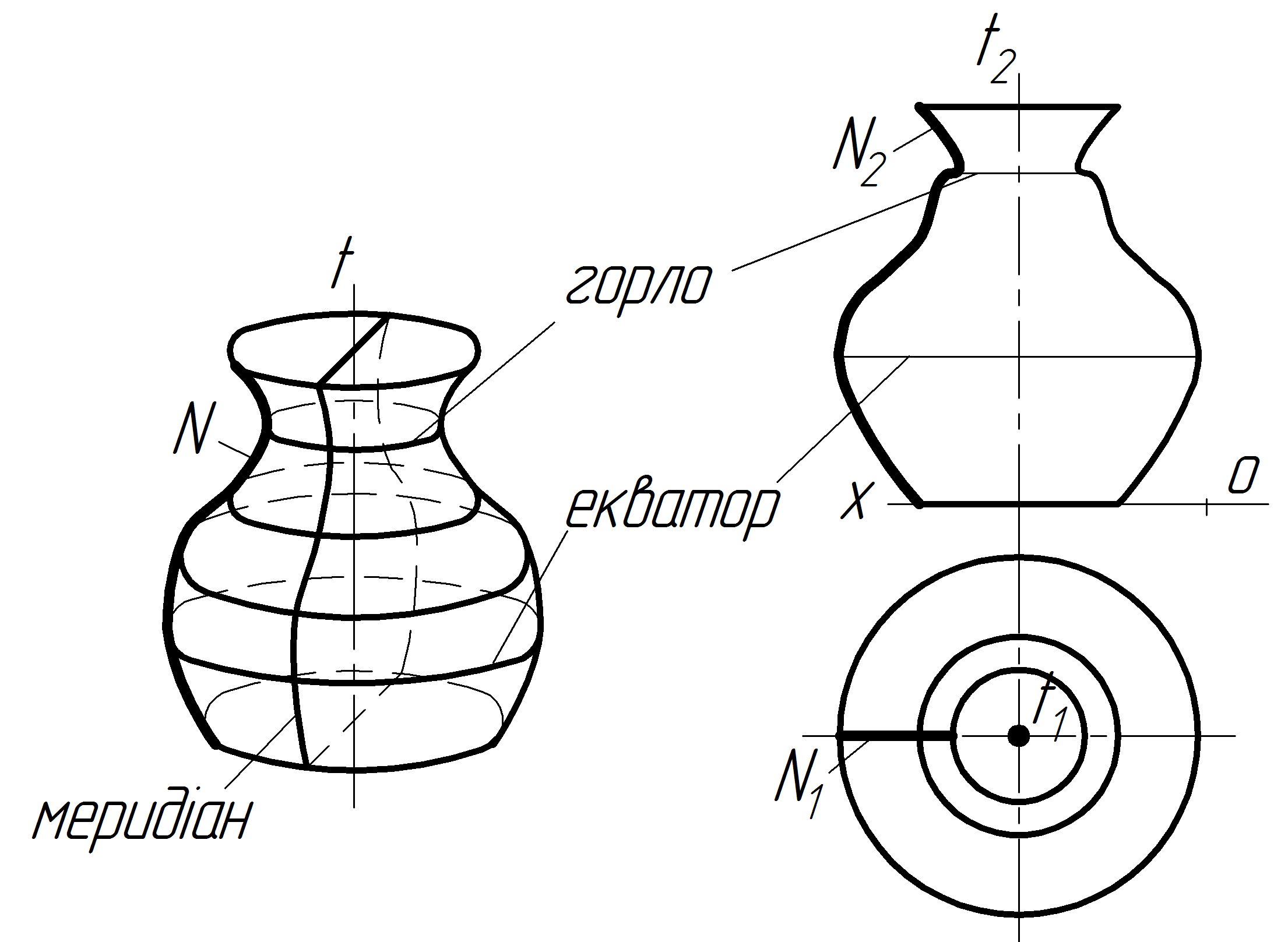
Поверхню, утворену обертанням будь-якої твірної лінії навколо нерухомої прямої – осі, називають поверхнею обертання.

На рисунку 7.12 зображено поверхню обертання довільного вигляду. Ця поверхня утворена обертанням будь-якої кривої K навколо осі. Найменшу паралель поверхні називають горлом, а найбільшу – екватором.

б)

а)

Рисунок 7.12 ― Утворення поверхні обертання

На рисунку 7.13 зображено сферичну поверхню (кулю), яка утворена обертанням кола навколо осі, що співпала з діаметром кола. Відрізок прямої, що сполучає центр кулі з будь-якою точкою її називають радіусом сфери (кулі). Усі точки сфери лежать на однаковій відстані від однієї точки – центра сфери.

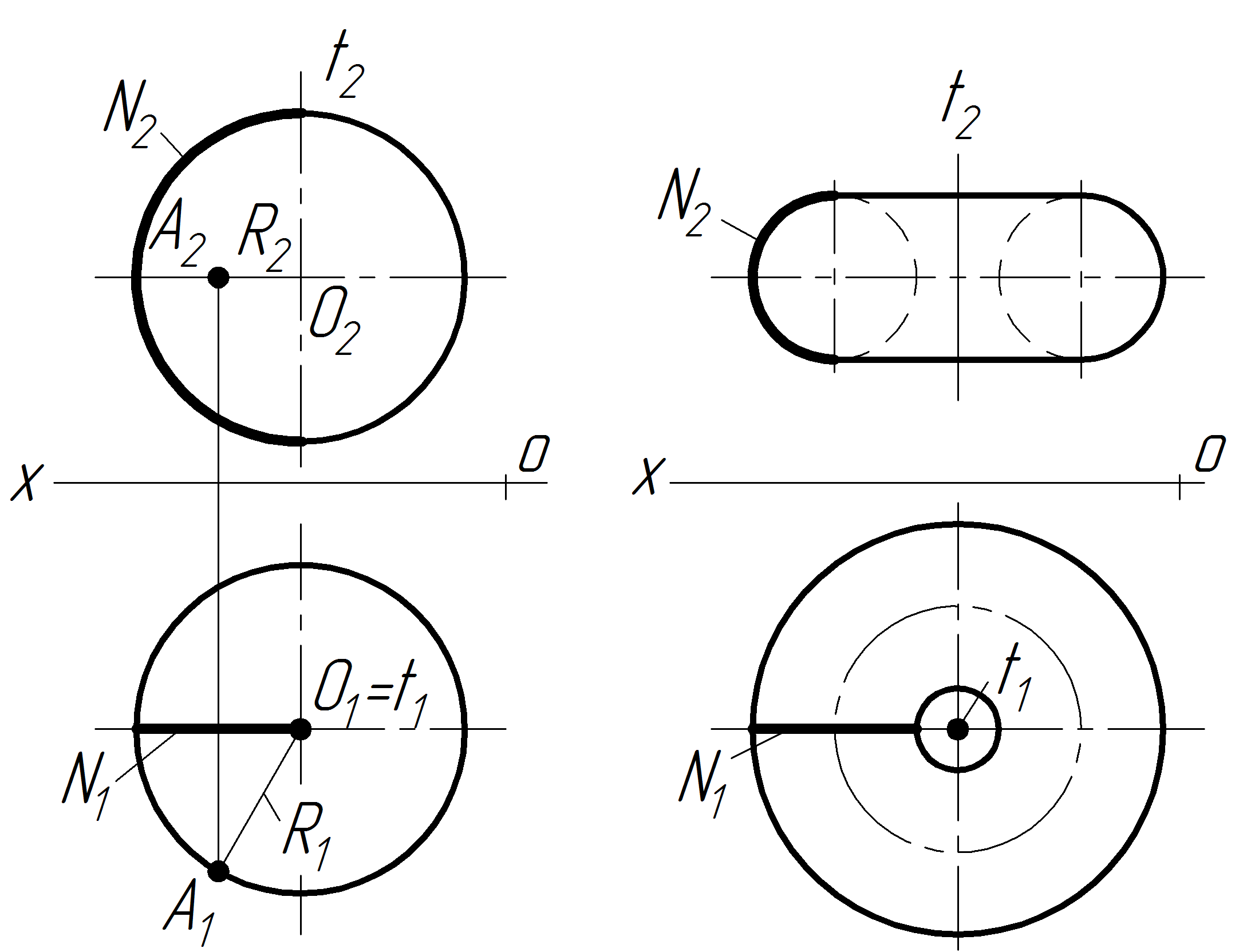
Рисунок 7.13 ― Утворення поверхні кулі

Рисунок 7.14 ― Утворення поверхні тора

До поверхонь обертання відноситься торова поверхня. Тор утворюється обертанням кола навколо осі, яка лежить у площині заданого кола і не проходить через його центр. Якщо вісь обертання розташована поза колом, то при обертанні утворюється тор-кільце, або колове кільце (форма камери автомобільної шини) (рис. 7.14). Тор-кільце називають відкритим.

Якщо ж вісь дотикається кола або перетинає його, але проходить через центр, то отримуємо коловий вал, або тор-яблуко. Нарешті, тор-лимон (бічні поверхні бочки) утворюється від обертання кругового сегмента навколо його хорди. Тор-яблуко називають закритим за умови дотику осі обертання до кола (рис. 7.15.) і самопересічним, якщо вісь перетинає коло. Також самопересічним є тор-лимон (рис.7.16).

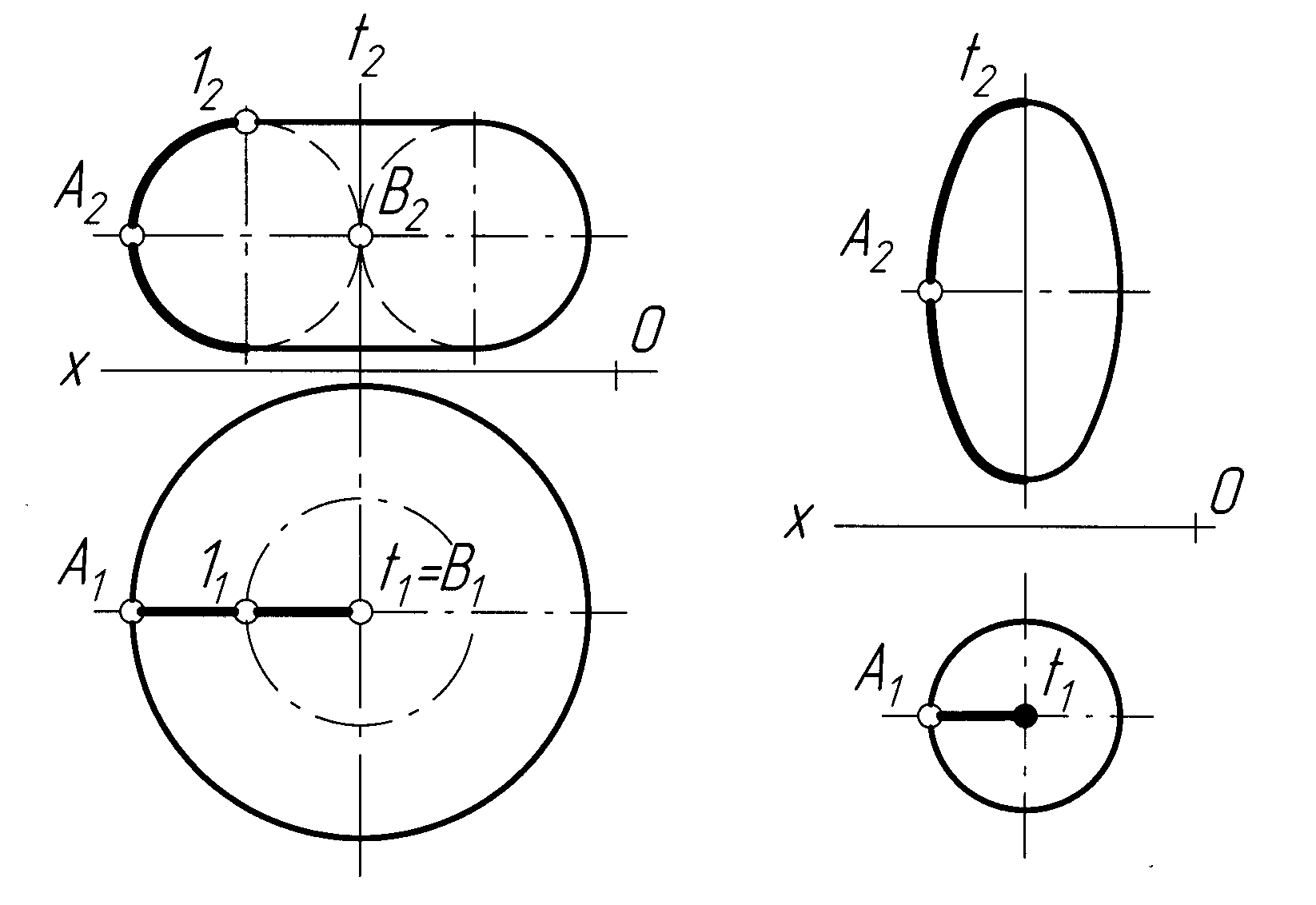
Рисунок 7.15 ― Різновиди

Торових поверхонь

Рисунок 7.16 ― Різновиди

Торових поверхонь

Закінчуючи виклад питань, пов’язаних утворенням і зображенням кривих поверхонь, згадаємо ще про деякі з них.

Еліпсоїд обертання – поверхня, яка утворена обертанням еліпса навколо малої або великої осі.

Подібно до еліпсоїда обертання утворюється параболоїд обертання та гіперболоїд обертання. Слід зазначити, що вісь обертання повинна проходити через вершину параболи при утворенні параболоїда обертання. Натомість гіперболоїд обертання може бути утворений обертанням гіперболи як навколо своєї осі, так і навколо уявної осі.

У першому випадку гіперболоїд складається з двох частин і називається двопорожнинним, а у другому - однопорожнинним.

Гвинтові поверхні утворюються рухом твірної – відрізка прямої – по двох напрямних, одна з яких є гвинтовою лінією, а друга – її віссю за умови обертання твірної навколо напрямної осі з одночасним ковзанням кінців напрямної по обох напрямних. На рисунку 7.17 зображено проекції такої поверхні, яка називається гвинтовим коноїдом або гелікоїдом.

Г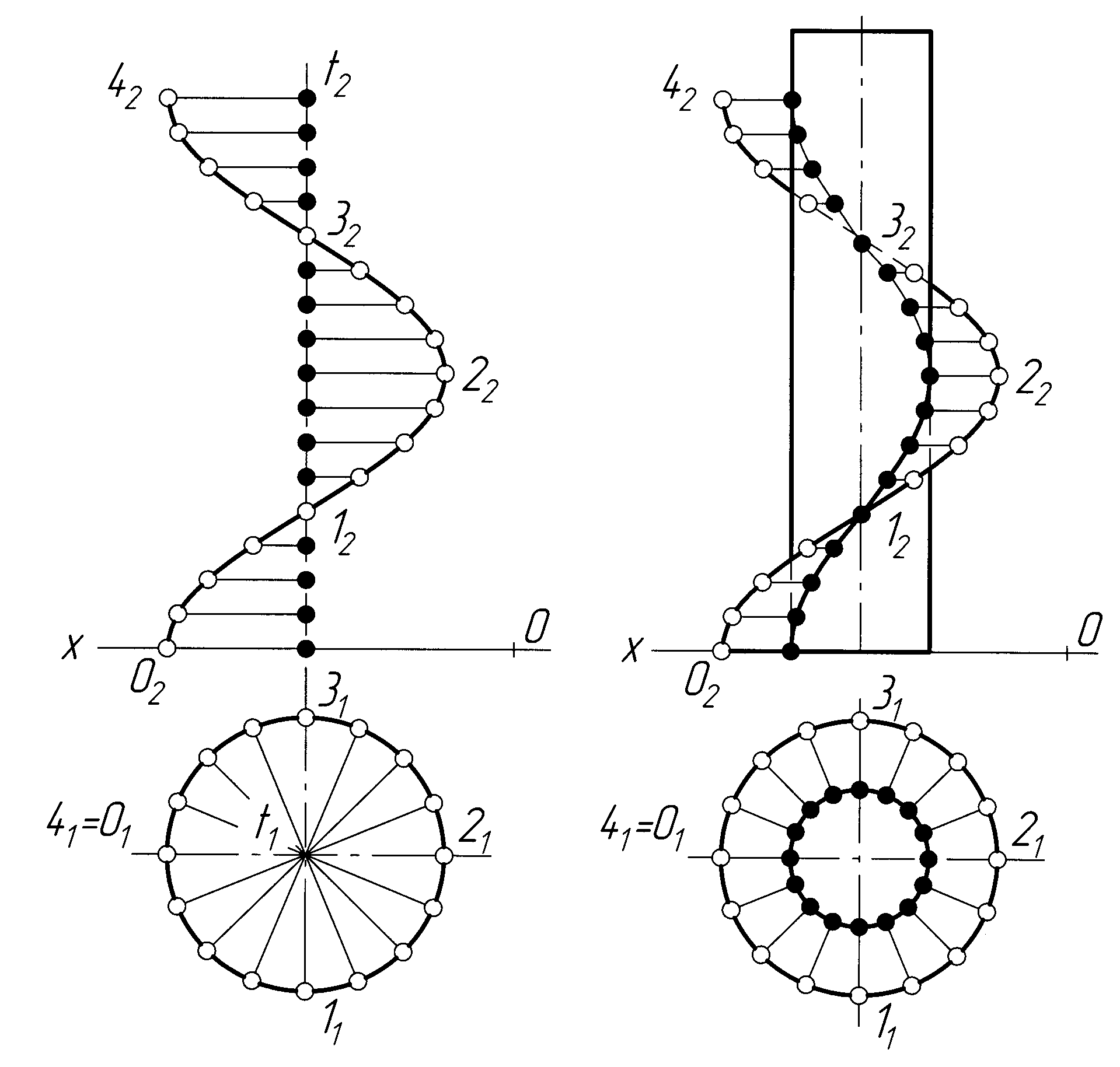 винтовий коноїд, утворений навколо піввісного з ним циліндра, називається кільцевим гвинтовим коноїдом. Прикладом застосування поверхні такого коноїда в техніці може бути переміщення сипучих, в’язких матеріалів або рідин (рис.7.17б).

а)

б)

Рисунок 7.17 ― Гвинтовий коноїд

До кривих поверхонь відносять і такі поверхні, як каркасні, топографічні, циклічні, канальні, трубчасті. Криві поверхні мають широке застосування в техніці, інженерних спорудах і конструкціях в геології, архітектурі, дизайні, декоративно-прикладному мистецтві тощо. Наприклад, каркасні поверхні використовуються при проеціюванні корпусів, кораблів, літаків, автомобілів і інших рухомих апаратах.