2 Ортогональні проекції точки

Основні положення проекції точки:

1. п рямокутною проекцією точки є основа перпендикуляра, який опущений з даної точки на площину проекцій (рис.2.1;)

2. проекцією точки завжди буде точка;

3. кожна точка має тільки одну проекцію на даній площині проекцій;

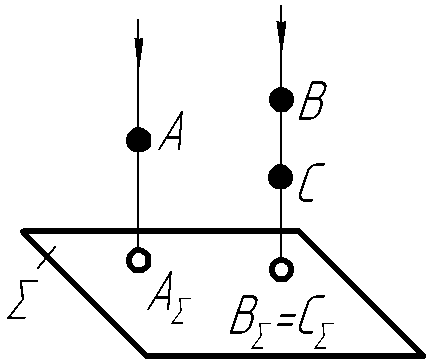
4. дві точки, розміщені на одному проекційному промені, проектуються в одну точку (рис.2.1).

О

Рисунок 2.1 - Ортогональне

Проеціювання точки на одну площину проекцій

дна проекція точки не визначає її положення в просторі відносно площин проекцій, тоді як дві проекції точки визначають положення самої точки відносно площин проекцій.

2.1 Проекція точки на дві площини проекцій, епюр точки

Множина двох (або більше) ортогональних проекцій точки (після суміщення площин проекцій) називається епюром (від французького epure – креслення). Більш загальне визначення епюра: зображення, яке отримуємо при суміщенні площин проекцій. На рисунку 2.2 показано епюр точки А, яка знаходиться в І чверті простору. При суміщенні площин проекцій проекції точки А (А₁ і А₂) розміщені по обидві сторони від осі ОХ і на одному перпендикулярі до неї. Відстань від проекції А₂ до осі ОХ на епюрі відповідає відстані від самої точки А до горизонтальної площини проекцій, відстань від проекції А₁ до осі ОХ відповідає відстані від самої точки А до фронтальної площини проекцій.

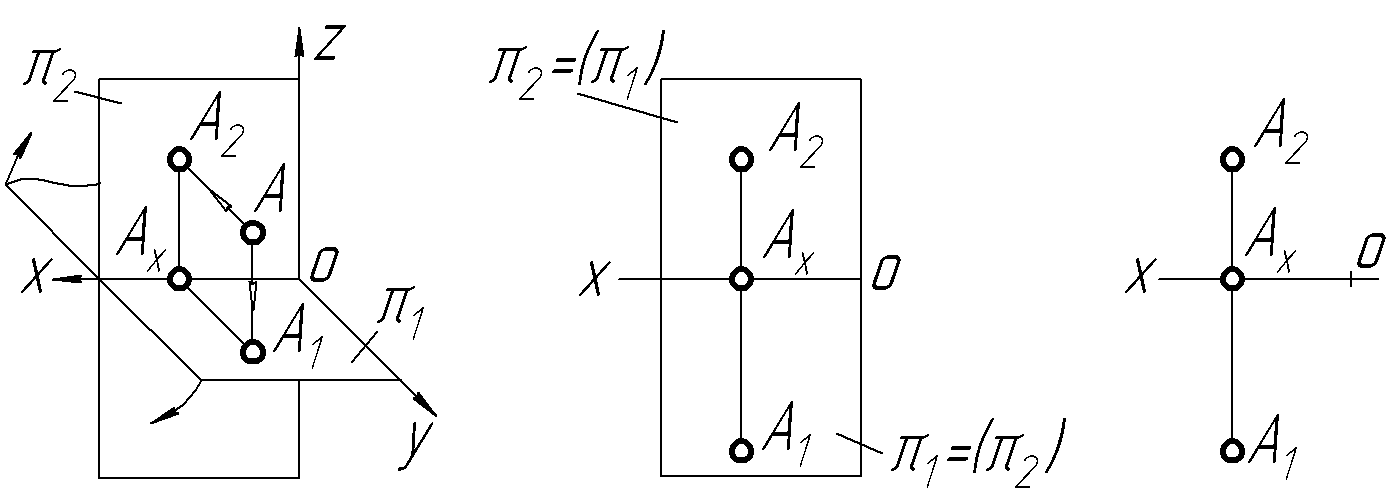
Рисунок 2.2 – Утворення епюра точки

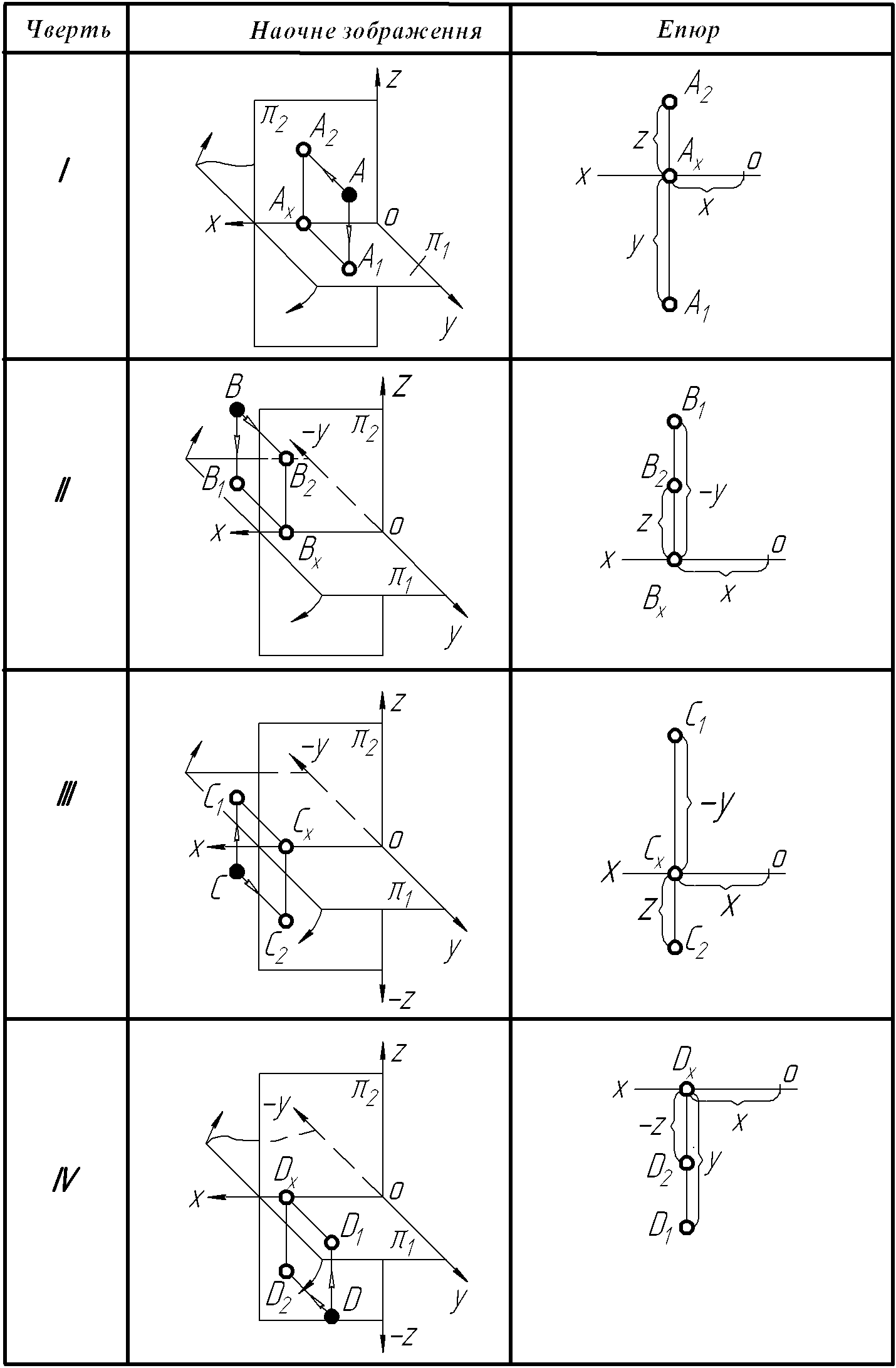
У таблиці 2.1 зведені приклади наочних зображень та епюрів точок А, В D, E, розміщених, відповідно, у І, ІІ, ІІІ, ІV чвертях простору. Точка А знаходиться в просторі І чверті, точка В – в ІІ чверті, точка D – в ІІІ чверті і точка E – в ІV чверті.

Таблиця 2.1 – Точка в чвертях простору

2.2 Проекції точок, які лежать у площинах проекцій

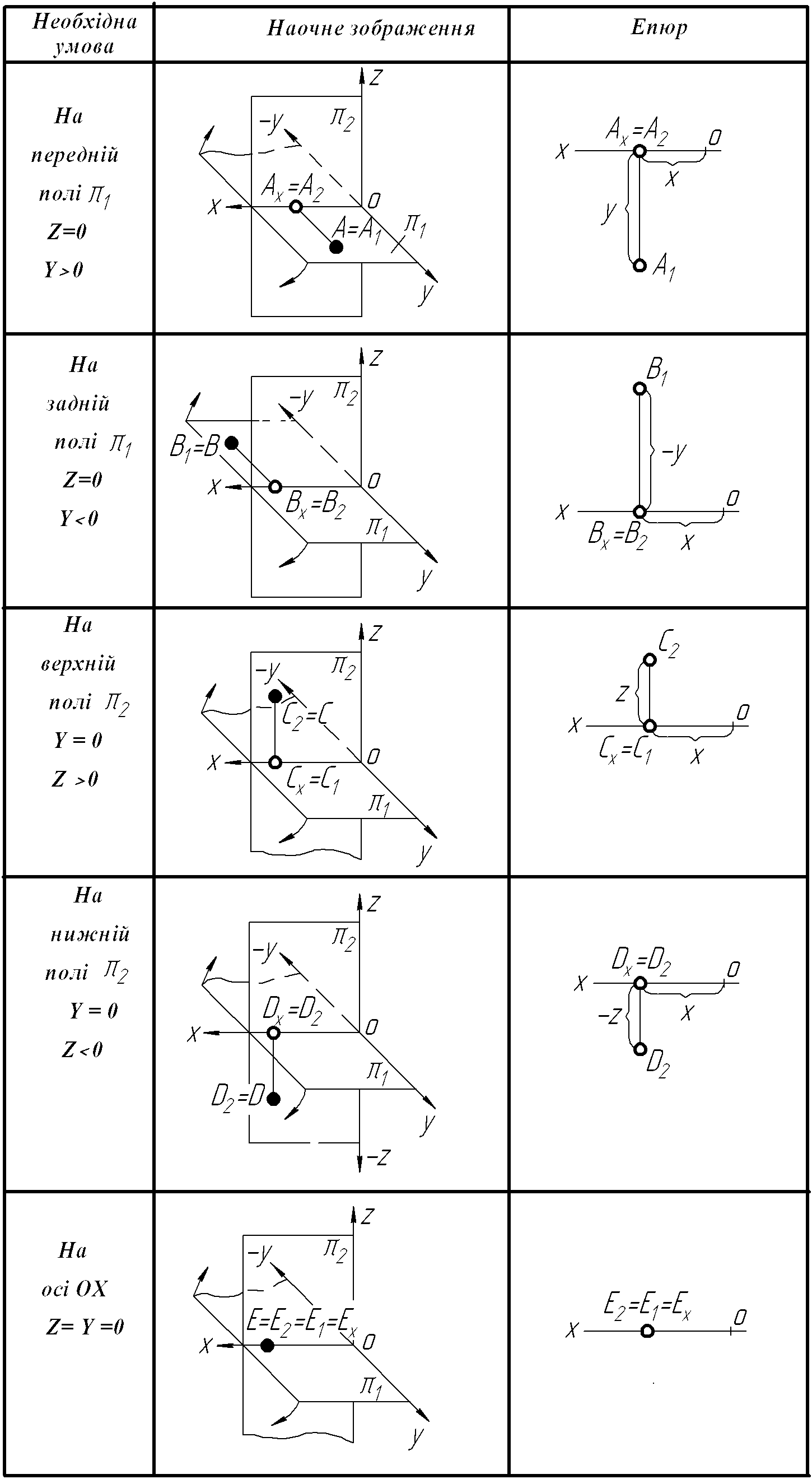
Якщо точка лежить у площині проекцій, то одна її проекція обов’язково збігається з даною точкою, а друга – лежить на осі проекцій. Наочні зображення і епюри точок, які лежать у площинах проекцій, показані в таблиці 2.2:

- точка А – в горизонтальній площині проекцій на її передній полі;

- точка В – в горизонтальній площині проекцій на її задній полі;

- точка С – у фронтальній площині проекцій на її верхній полі;

- точка D – у фронтальній площині проекцій на її нижній полі;

- точка Е – на осі проекцій (одночасно лежить на двох площинах проекцій, тому обидві проекції точки Е збігаються з даною точкою).

Таблиця 2.2 – Проекції точок, які лежать у площинах проекцій

Задача. Побудувати наочне зображення та епюр точки С, яка симетрична точці А(25, 30, 15) відносно ₁, та епюр точки В, яка симетрична точці А відносно ₂.

Згідно з умовою задачі координати точки А додатні, отже точка знаходиться в І чверті. Точка С, яка буде симетрична точці А відносно ₁, матиме такі ж самі координати за абсолютною величиною, але координата Z змінить свій знак на протилежний. Отже, точка В знаходитиметься в ІV чверті. Точка В, яка симетрична точці А відносно фронтальної площини проекцій, розміщена в ІІ чверті, а, отже, координата Y змінить свій знак на протилежний. Розв’язок задачі поданий у таблиці 2.3.

Таблиця 2.3 – Розв’язок задачі