4. Нормальний розподіл (Гауса)

Нормальний розподіл застосовують в теорії надійності для опису подій, що залежать від багатьох факторів, кожен з яких слабо впливає на розподіл випадкової події.

За нормальним законом розподіляються параметри серійної продукції, відмови обладнання в результаті зносу та ін.

Щільність розподілу нормального закону описується наступною формулою

, (16)

де – математичне чекання, а  ² – дисперсія випадкової величини.

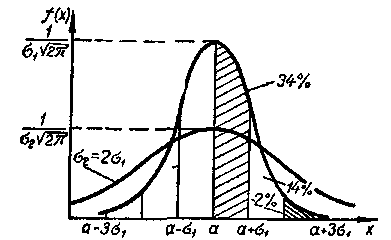
Розподіл залежить від двох параметрів – і . Крива щільності розподілу f(x) (рис. 4а) є симетричною відносно математичного чекання, і її максимальне значення, як випливає з формули (13), дорівнює . Чим більша дисперсія, тим більш плоскою є крива щільності розподілу.

а б

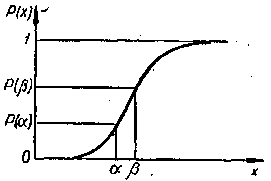
Рис. 4. Крива щільності (а) та функції (б) розподілу випадкової величини з нормальним законом розподілу.

5. Розподіл Пуассона

Розподіл Пуассона характеризує дискретну випадкову величину (величину, що може приймати певну множину значень), і широко використовується в теорії надійності для визначення ймовірності появи потоку подій (відмов).

Якщо незалежні події відбуваються з певною середньою частотою , то ймовірність Р_m (за певний відрізок часу t відбудеться рівно m подій) визначається по закону Пуассона. Наприклад, кількість повітряних суден, що здійснюють посадку в аеропорті за 1 годину і таке інше.

Закон розподілу записується у такому вигляді:

(17)

Графічно розподіл Пуассона для різних значень  представлено на рис. 5.

Рис. 5. Графіки розподілу Пуассона для різних значень .

6. Біноміальний розподіл.

Біноміальний розподіл також характерний тільки для дискретних випадкових величин. Розподіл ймовірностей є біноміальним в разі, якщо його члени відповідають розкладенню бінома (p + q)ⁿ, де значення p і q – ймовірності появи або не появи події в кожному з n досвідів.

Сума всіх членів розкладення тотожно дорівнює одиниці, адже (p+q)ⁿ = 1ⁿ_, а кожен член розкладення являє собою певну ймовірність, що розраховується за формулою

,

де Р_{m, n} – ймовірність того, що при загальній кількості n досвідів подія відбудеться рівно m раз;

– кількість сполучень з n по m;

р – постійна ймовірність появи події у кожному досвіді;

q=1- p – ймовірність не появи події у кожному досвіді.

Таким чином перший член розкладення рⁿ представляє собою ймовірність того, що подія виникне в усіх n досвідах, другий член np^n-1q – ймовірність того, що подія відбудеться у n - 1 досвідах і в одному не відбудеться і т.д.

Математичне чекання та дисперсія біноміального розподілу знаходяться відповідно за формулами M[n] = np; D[n] = npq.

Графічно приклад біноміального розподілу для n = 20 та різних значень р зображено на рис. 6 [2].

Рис. 6. Приклад графіків біноміального розподілу для різних значень р.

Порядок виконання роботи

1. Ознайомитися з основними законами розподілу випадкових величин, що застосовуються в теорії надійності та проаналізувати їх основні властивості.

2. Лабораторна робота виконується з застосуванням комп'ютерної програми Excel. При відкритті відповідної сторінки (Лист1 – Лист 4) та введенні вихідних даних, програма моделює випадкову величину з певним законом розподілу та будує графік її функції або щільності розподілу. Необхідно задати параметри випадкової величини у відповідних віконцях, які позначено синім кольором і занести в протокол (або роздрукувати) графік, який видає комп'ютерна програма.

До віконця F(x)/f(x) має бути занесений логічний параметр “ИСТИНА” – в цьому випадку програма видає графік функції розподілу випадкової величини, або “ЛОЖЬ” – тоді програма видає графік щільності розподілу випадкової величини.

Приклад сторінки Excel для моделювання, наприклад, показового розподілу випадкової величини, наводитися на рис.7.

3. Побудувати графіки щільності розподілу випадкової величини (всі графіки, що відповідають закону або щільності розподілу випадкової величини на одній координатній сітці) і дослідити, як значення параметра закону розподілу впливає на форму графіка функції та щільності розподілу випадкової величини.

4. Визначити математичне чекання, дисперсію та середньоквадратичне відхилення випадкової величини за графіком та аналітично для випадків, коли це необхідно з застосуванням формул (7 - 9).

5. За результатами лабораторної роботи зробити висновки.