1.4. Решение задач лп средствами excel

1.4.1. Решение одноиндексных задач

1. Ввод условий задачи:

l₁ ≤ x₁ ≤ d₁, l₂ ≤ x₂ ≤ d₂, …, l_n ≤ x_n ≤ d_n.

1. Создание формы для ввода условий задачи.

ПЕРЕМЕННЫЕ
имя	имя 1	имя 2	…	имя n
значение
ниж. гр.	l1	l2	…	ln
вер. гр.	d1	d2,	…	dn.
коэф. в ЦФ	c1	с2	…	сn	Функция, реализующая целевую функцию	направление оптимизации (max, min)
ОРГАНИЧЕНИЯ
Название ограничения					Функция, реализующая левую часть	знак	Прав. часть
1	a11	a12	…	a1n	1-го ограничения		b1
2	a21	a22	…	a2n	2-го ограничения		b2
…	…	…	…	…	…	…	…
n	am1	am2	…	amn	n-го ограничения		bm

2. Ввод исходных данных. Заполняются ячейки, содержащие: нижние и верхние границы переменных, коэффициенты целевой функции, коэффициенты ограничений, знаки ограничений, направление оптимизации целевой функции.

3. Вод зависимостей из математической модели. Заполняются ячейки содержащие: функцию; реализующую целевую функцию задачи; функции, реализующие левые части ограничений задачи.

3.1. Вод зависимости для целевой функции.

3.1.1. Поместить курсор в ячейку, отведенную под значение целевой функции.

3.1.2. Выбрать кнопку Мастер функций.

3.1.3. Выбрать функцию СУММПРОИЗВ и заполнить диалоговое окно. В массив 1 нужно ввести диапазон ячеек, содержащих значения переменных. В массив 2 ― диапазон ячеек, содержащих коэффициенты целевой функции.

3.2. Ввод зависимостей для левых частей ограничений.

3.2.1. Поместить курсор в ячейку, отведенную под левую часть ограничения.

3.2.2. Выбрать кнопку Мастер функций.

3.2.3. Выбрать функцию СУММПРОИЗВ.

3.2.3. Заполнить диалоговое окно функции СУММПРОИЗВ. В массив 1 нужно ввести диапазон ячеек, содержащих значения переменных (использовать при этом абсолютные ссылки). В массив 2 ― диапазон ячеек, содержащих коэффициенты данного ограничения.

3.2.4. Копировать содержимое ячейки в буфер.

3.2.5. Вставить содержимое буфера в ячейки, отведенные под левые части остальных ограничений.

4. Ввод основных параметров модели в диалоговом окне Поиск решения.

4.1. Войти в меню Сервис и выбрать пункт Поиск решения.

Если виданном мену нет Поиска решения, то выбрать пункт Надстройка и в появившемся диалоговом окне выставить флажок Поиск решения. Нажать кнопку ОК.

4.3. Заполнить параметры диалогового окна Поиск решения.

4.4.1. В пункте установить целевую ячейку, отведенную под целевую функцию.

4.4.2. В соответствии с решаемой задачей выбрать направление целевой функции.

4.4.3. Нажать кнопку Добавить. Появиться диалоговое окно для построения ограничений задачи. В левой части указывается ячейка (группа ячеек), в которой содержится левая часть ограничения, в центре выбирается знак ограничения, в правой части ― ячейка (группа ячеек) с правой частью ограничения. После ввода каждого ограничения нужно нажимать на кнопку Добавить. Когда все ограничения задачи построены, нужно нажать на кнопку ОК и вернуться в диалоговое окно Поиск решения.

4.4.4. Нажать кнопку Параметры диалогового окна Поиск решения. Появится диалоговое окно Параметры поиска решения. С помощью команд, находящихся в этом диалоговом окне, можно вводить условия для решения задач оптимизации всех классов. В ряде пунктов данного окна записаны значения, используемее по умолчанию, которые подходят для большей части практических задач.

4.4.5. Установить флажок Линейная модель. Это обеспечит применение симплекс-метода.

4.4.6. Нажать кнопку Выполнить. Начинается решение составленной математической задачи. Через какое-то время появиться диалоговое окно Результаты поиска решения. Нужно выбрать интересующие виды отчетов по решению задачи и проанализировать полученное решение. Каждый из видов отчетов создается на отдельном листе.

Если при заполнении полей окна "Поиск решения" были допущены ошибки, не позволяющие Excel применить симплекс-метод для решения задачи или довести ее решение до конца, то после запуска задачи на решение на экран будет выдано соответствующее сообщение с указанием причины, по которой решение не найдено.

Отчет по результатам состоит из трех таблиц.

Таблица 1 приводит сведения о целевой функции. В столбце Исходно приведены значения целевой функции до начала вычисления.

Таблица 2 приводит значения искомых переменных, полученных в результате решения задачи.

Таблица 3 показывает результаты оптимального решения для системы ограничений и для граничных условий.

Отчет по устойчивости состоит из двух таблиц.

В Таблице 1 приводятся следующие значения переменных:

1. результат решения задачи;

2. редуцированная стоимость, т.е. дополнительные двойственные переменные, которые показывают, насколько условных единиц изменится целевая функция при принудительном включении единицы этой продукции в оптимальное решение;

3. коэффициенты целевой функции (стоимости);

4. предельные значения приращения каждого коэффициента целевой функции, при которых сохраняется набор базисных переменных в оптимальном решении.

В Таблице 2 приводятся:

1. величина используемых ресурсов;

2. теневая цена, т.е. двойственные оценки, которые показывают, как измениться целевая функция при изменении ресурса на единицу;

3. значения приращения каждого ресурса, при которых сохраняется оптимальный набор переменных, входящих в оптимальное решение.

Отчет по пределам показывает, в каких пределах может изменяться выпуск продукции, вошедшей в оптимальное решение, при сохранении структуры оптимального решения.

Пример 18. Продукцией молочного завода являются молоко, кефир и сметана. На производство 1 т молока, кефира и сметаны требуется соответственно 1,01; 1,01; 9,45 т молока. Затраты рабочего времени при разливе 1 т молока и кефира составляют 0,17 и 0,18 машино-час. Расфасовка 1 т сметаны на специальном автомате занимает 3,15 час. Всего за сутки молочный завод может переработать 140 т молока. Основное оборудование может быть занято в течение 21,0 машино-часа, а автомат по расфасовке сметаны - в течение 16 час. Прибыль от реализации 1т молока, кефира и сметаны соответственно равна 31, 23 и 137 руб. Завод должен производить ежедневно не менее 90 т молока в сутки. Требуется определить объемы выпуска молочной продукции каждого вида, позволяющие получить наибольшую прибыль.

Решение. Экранная форма для ввода условий задачи вместе с введенными в нее исходными данными представлена на рис. 2.

Рис. 2. Экранная форма задачи

В ячейку E7, в которой будет отображаться значение ЦФ, необходимо ввести формулу СУММПРОИЗВ(B2:D2;B7:D7), по которой это значение будет рассчитано. В ячейку E11 вводим формулу СУММПРОИЗВ($B$2:$D$2;B12:D12) и растягиваем вниз в ячейки E12; E13 (рис. 3). Для ввода формул воспользуемся «Мастер функций f_x», в окне "Категория" выбираем "Математические"; в окне "Функция" выберите функцию СУММПРОИЗВ; в появившемся окне в строку "Массив 1" вводим выражение B$2:D$2, а в строку "Массив 2" – выражение B7:D7 (рис. 1.3). В экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).

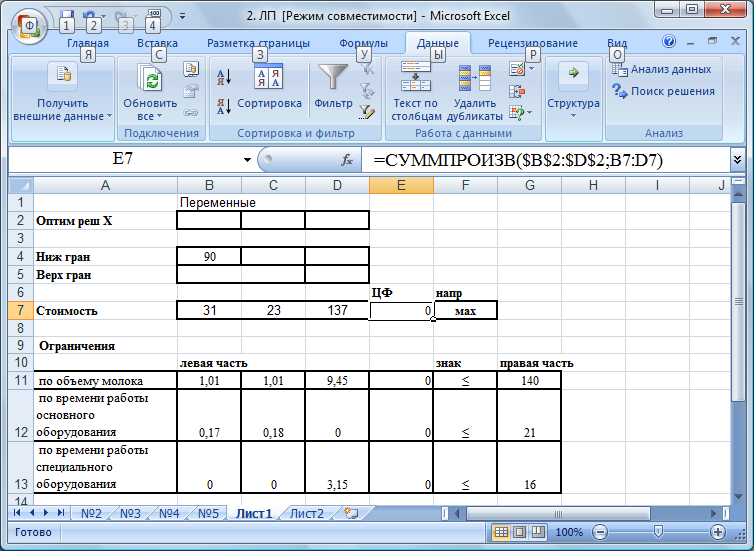
Рис. 3. Экранная форма после ввода всех необходимых формул

Дальнейшие действия производятся в окне «Поиск решения» (рис. 4).

В вкладке Параметры установить флажок «Линейная модель» и «Неотрицательные значения», что обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода (рис. 5).

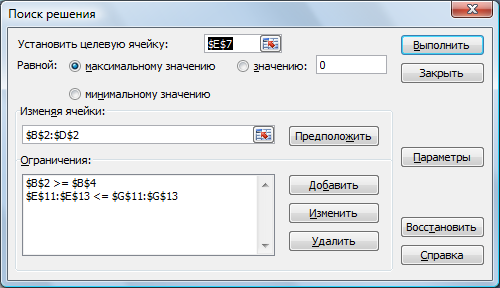
Рис. 4. Окно "Поиск решения" после ввода всех данных

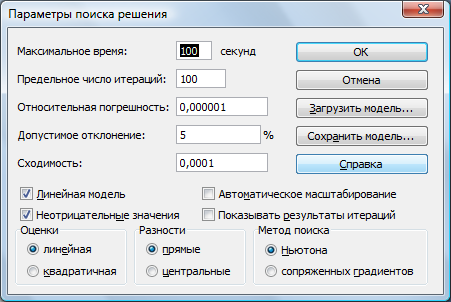
Рис. 5. Параметры поиска решения

Запускаем решение задачи путем нажатия кнопки «Выполнить», выбирая два отчета (рис.6).

Рис. 6. Результаты поиска решений

После этого в экранной форме появляется оптимальное решение задачи (рис. 7).

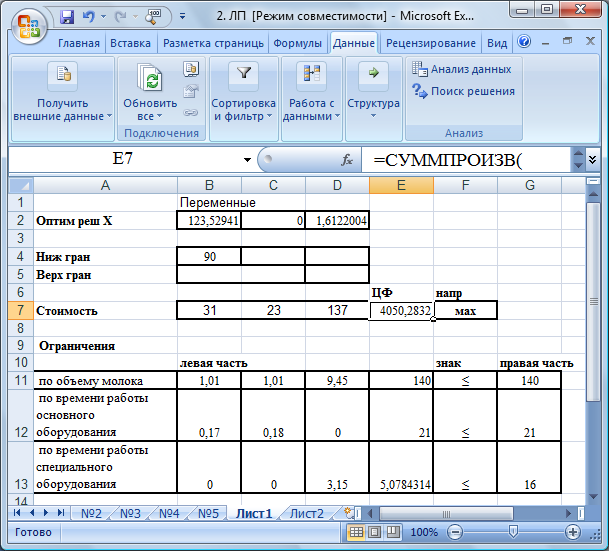
Рис. 7. Экранная форма задачи после получения решения

Таким образом, оптимальное решение Х = (123,53; 0; 1,61); F_max = 4050,28 рублей. Рентабельной продукцией является молоко и сметана, выпуск кефира не выгодно.

Пример 19. Из 500 листов железа 1-го размера и 300 листов железа 2-го размера несколькими способами выкраиваются 3 вида деталей. Даны нормы одновременного выхода деталей по различным способам в таблице 12. Определить максимальное число комплектующих деталей, если комплект состоит из 4-х деталей вида 1, 3-х деталей вида 2 и 2-х деталей вида 3.

Таблица 12

Вид детали	Способы раскроя
	1	2	3	1	2
	Количество деталей
1	0	2	9	6	5
2	4	3	4	5	4
3	6	16	0	8	0

Решение. Пусть х_i – количество бревен i-го распила, х – число комплектов брусьев. Тогда F = х → max

2 х₂ + 9х₃ +6х₄ + 5х₅ = 4х

4х₁ + 3х₂ +4х₃+ 5х₄ +4х₅ = 3х

6х₁ + 16х₂ + 8х₄ = 2х

х₁ + х₂ + х₃ ≤ 500

х₄ + х₅ ≤ 300

√x_i ≥ 0

Экранная форма для ввода условий задачи вместе с введенными в нее исходными данными представлена на рис. 8.

Рис. 8. Экранная форма ввода условий

В ячейку G6, в которой будет отображаться значение ЦФ, необходимо сделать ссылку на ячейку G7, по которой это значение будет рассчитано. В ячейку B6 вводим формулу СУММ(B5:D5), а в Е6 вводим формулу СУММ(E5:F5).

В ячейку G9 вводим формулу СУММПРОИЗВ($B$5:$F$5;B9:F9) и растягиваем вниз в ячейки G10; G11. В ячейку I10 вводим формулу G9-H9*$G$5 и растягиваем вниз в ячейки I11; I12.

Дальнейшие действия производятся в окне «Поиск решения» (рис. 9). В вкладке Параметры установить флажок «Неотрицательные значения», что обеспечивает ускорение поиска решения линейной задачи за счет применение симплекс-метода.

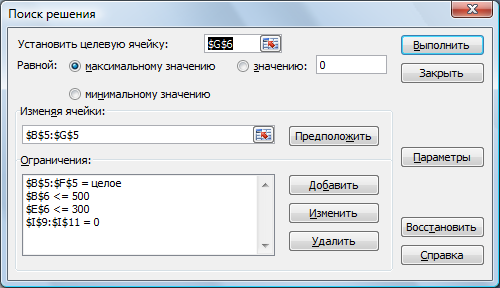
Рис. 9. Экранная форма Поиска решений

После этого в экранной форме появляется оптимальное решение задачи (рис. 10).

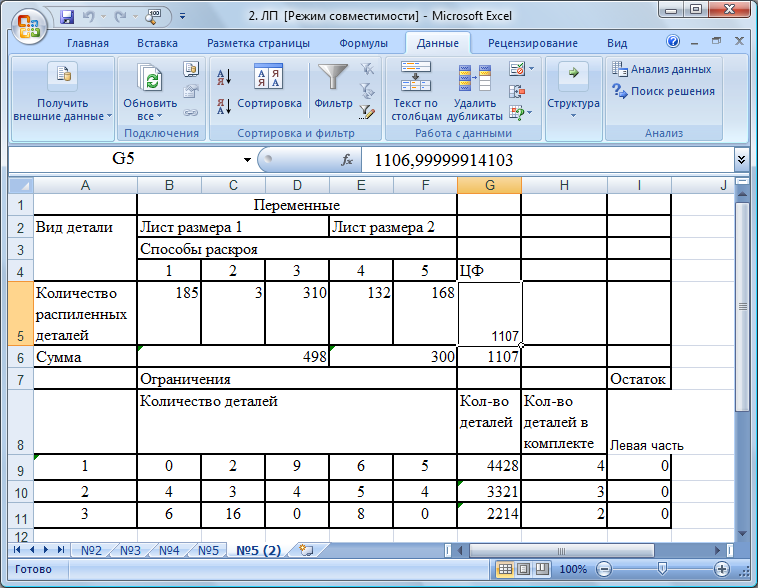
Рис. 10. Экранная форма задачи после получения решения

Таким образом, оптимальное решение Х = (185; 3; 310; 132; 168); F_max = 1107 изделий.