1.5.2. Теоремы двойственности

Первая теорема двойственности.

а) Если одна из пары двойственной задачи разрешима, то разрешима и другая, причем Z_max = F_min.

б) если одна из пары двойственной задачи неограниченна сверху (Z_max = + ∞), то другая задача неразрешима, по причине несовместимости системы ограничений в области допустимых решений.

Экономический смысл теоремы: план производства Х и набор цен ресурсов У оказывается оптимальным тогда и только тогда, когда прибыль от продукции, найденная при внешних ценах с_j равна затратам на ресурсы по внутренним ценам у_i.

Вторая теорема двойственности. Для того, чтобы планы Х и У пары двойственных задач были оптимальными, необходимо и достаточно выполнение условий:

. (12)

Отсюда следует, что положительными (ненулевыми) компонентами оптимального решения одной из возможных двойственных задач соответствует нулевые компоненты оптимального решения другой задачи, т.е. для любого i и j при х*_j>0 → у*_m+j = 0 и, наоборот, при у*_j>0 → х*_n+i = 0.

Экономический смысл: если по некоторому оптимальному плану Х производство расходов i-го ресурса строго меньше его запаса b_i то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане оценок его i-я компонента строго больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда вывод: дефицитный ресурс имеет положительную оценку, а ресурс избыточный нулевую оценку.

Третья теорема двойственности (об оценках):

Двойственные оценки показывают приращение функции цели, вызванное малым изменением свободного члена соответствующего ограничения: (13)

или ΔF = Δb_i*y_i.

Свойство 1. Оценка является мерой дефицитности ресурсов. Чем выше величина оценки y_i, тем выше дефицитность i-го ресурса.

Свойство 2. Оценка есть мера влияния ограничений на значение целевой функции. Величина двойственной оценки какого-либо ресурса показывает, насколько возросло бы максимальное значение целевой функции, если бы объем данного ресурса увеличился на единицу.

Свойство 3. Оценки есть мера относительной взаимозаменяемости ресурсов. Например, отношение y_i/y_k показывает, сколько единиц k-го ресурса может быть высвобождено при увеличении объема i-го ресурса на единицу, для того чтобы максимум целевой функции остался на прежнем уровне.

Свойство 4. Оценка есть инструмент определения эффективности новых технологических способов производства. Если

, (14)

вариант производства является выгодным, если Δ_j > 0 – вариант невыгоден, где a_ij число единиц нового ресурса.

1.5.3. Объективно обусловленные оценки и их смысл

Пример 25. Для изготовления двух видов продукции Р₁ и Р₂ используются четыре вида ресурсов. Запасы ресурсов, нормы затрат на 1ед. продукции данного вида и цена на 1ед. продукцию каждого вида приведены в табл. 16:

Таблица 16

Вид ресурса	Число единиц ресурсов на 1 ед. прод.		Запас
	Р1	Р2
S1	1	3	18
S2	2	1	16
S3	-	1	5
S4	3	-	21
Цена 1ед. прод.	2	3

Решение. 1. Составим исходную и двойственную модель.

F = 2х₁ + 3х₂à max Z = 18y₁ + 16y₂ + 5y₃ + 21y₄ à min

x ₁ + 3x₂ ≤ 18 y₁ + 2y₂ + 3y₄ ≥ 2

2x₁ + x₂ ≤ 16 3y₁ + y₂ + y₃ ≥ 3

x₂ ≤ 5 любое y_i ≥ 0

3x₁ ≤ 21

х₁ ≥ 0, х₂ ≥ 0.

Экранная форма для ввода условий задачи вместе с введенными в нее исходными данными представлена на рис. 17. В ячейку D4, в которой будет отображаться значение ЦФ, необходимо ввести формулу СУММПРОИЗВ($B$2:$C$2;B3:C3), по которой это значение будет рассчитано. В ячейку D7 вводим формулу СУММПРОИЗВ($B$2:$C$2;B7:C7) и растягиваем вниз в ячейки D8; D9; D10. Дальнейшие действия производим в окне «Поиск решения» (рис. 18).

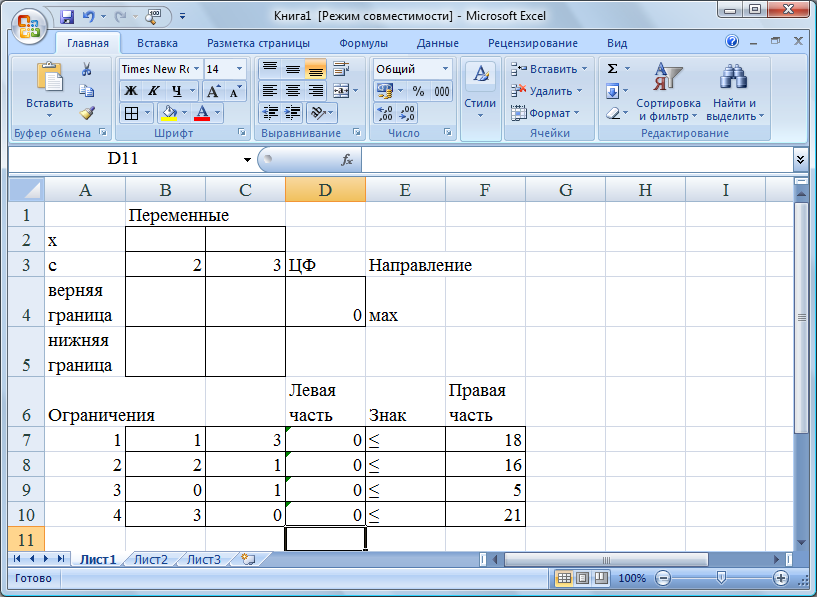
Рис. 17. Экранная форма после ввода всех необходимых формул

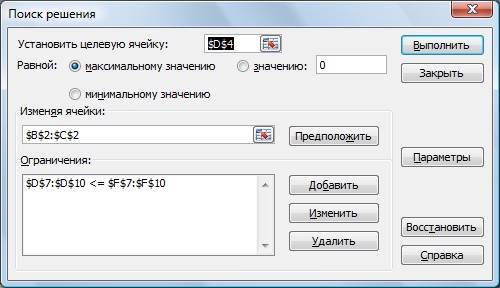
Рис. 18. Окно "Поиск решения" после ввода всех данных

Запускаем решение задачи путем нажатия кнопки «Выполнить», выбирая два отчета.

После этого в экранной форме появляется оптимальное решение задачи (рис. 19).

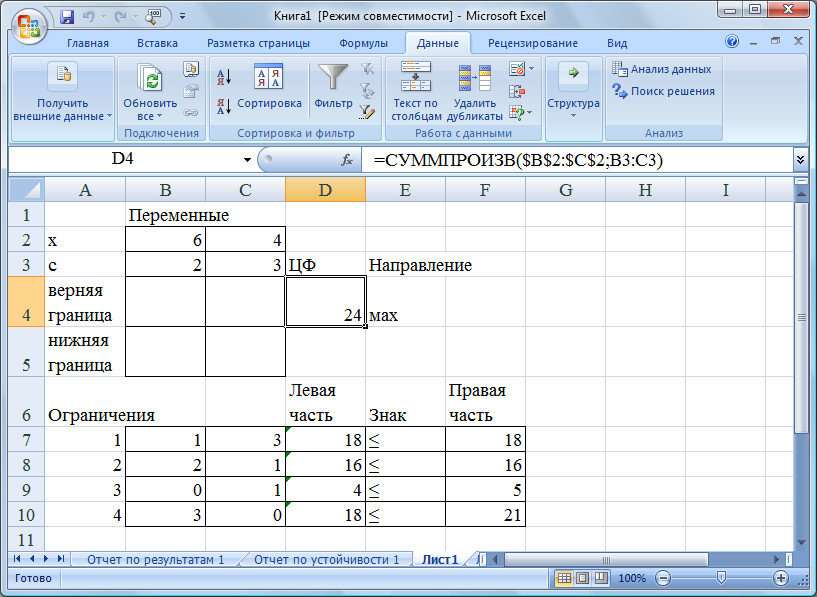
Рис. 19. Экранная форма оптимального решения

Таким образом, оптимальное решение Х = (6; 4); F_max = 24 рублей. Отчет по устойчивости (рис. 20) дает значение теневой цены У_опт = (0,8;0,6;0;0).

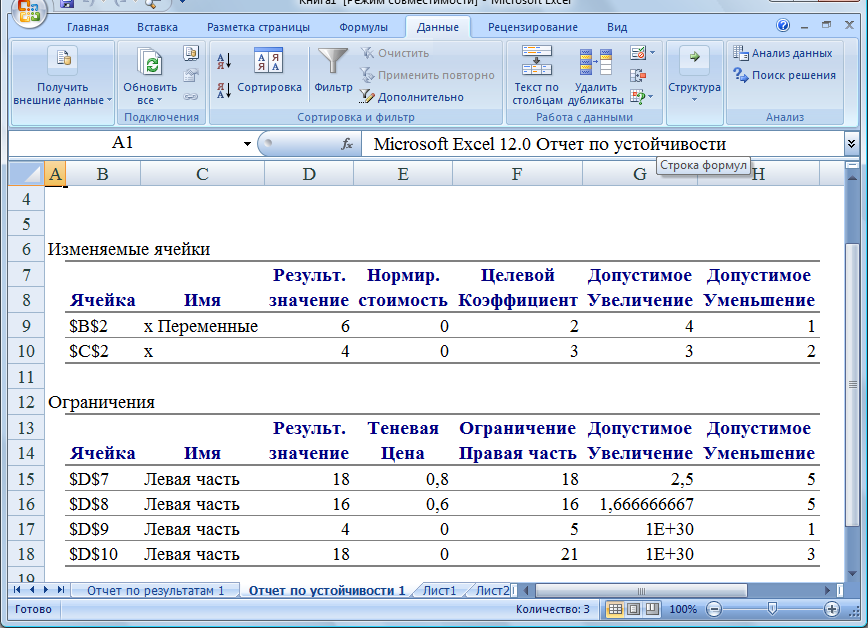
Рис. 20. Отчет по устойчивости

Изменение ресурсов прямой задачи может оказать влияние, как на ее оптимальный план, так и на систему оптимальных двойственных оценок. Поэтому чтобы проводить экономический анализ нужно знать их интервал устойчивости. Изменение прибыли и новое оптимальное решение можно найти в том случае, если изменение ресурса не выходит за пределы устойчивости, так как двойственные оценки останутся прежними.

Предельное изменение стоимости (рис. 20):

с₁ = 2 → → .

с₂ = 3→ → .

Предельное изменение по ресурсам (рис. 20):

b₁ = 18 → ; ;

b₂ = 16 → ; 11 ≤ b₂ ≤ ;

b₃ = 5→ ; ;

b₄ = 21→ ; .

2. Дадим экономическую интерпретацию двойственных задач.

2.1. Дефицитность продукции и ресурсов

Так как х₁ = 6 и х₂ = 4 > 0, то выпускать продукцию Р₁ и Р₂ рентабельно (если бы основная переменная х_i равнялась нулю, то продукцию Р_i выпускать было бы не целесообразно). На рис. 21 статус «связан» означает, что данный ресурс является дефицитным. Следовательно, ресурсы S₁ и S₂ являются дефицитными, а ресурсы S₃ и S₄ являются недефицитными

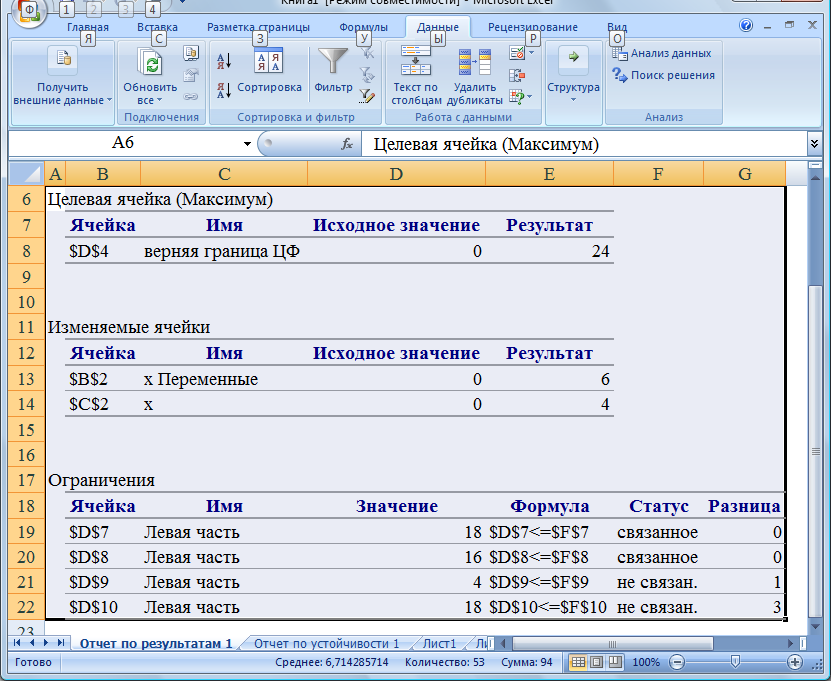
Рис. 21. Отчет по результатам

Основные переменные у₁, у₂ положительны, следовательно ресурсы S₁ и S₂ являются дефицитными, основные переменные у_3, у₄ равны нулю, тогда ресурсы S₃ и S₄ являются недефицитными. Так как у₁ > у₂, то по третьей теореме двойственности (свойство 1) ресурс S₁ более дефицитен, чем S₂. Следовательно, наиболее выгодно увеличение объемов ресурса S₁.

2.2. Прирост прибыли при изменении ресурсов.

Увеличение S₁ на одну единицу ( ) увеличит прибыль по третьей теореме двойственности на ΔF₁ = 4/5*1 = 4/5 руб., т.е. общая стоимость F = 24 + 0,8 = 24,8 руб.

Увеличение S₂ на одну единицу ( ) увеличит прибыль на ΔF₂ = 3/5*1 = 3/5 руб., т.е. F = 24 + 0,6 = = 24,6 руб.

Увеличение S₃ и S₄ не изменит прибыль, так как ΔF₃ = 0*1=0; ΔF₄ = 0*1 = 0.

Увеличение одновременно первого и второго ресурса на 5 единицы приведет к увеличению прибыли на ΔF = 4/5*5+3/5*5 = = 7 руб., т.е. общая стоимость F = 24 + 7 = 31 руб.

2.3. Взаимозаменяемость ресурсов. Если бы S₁ уменьшилось на 1 единицу, то падение выручки можно компенсировать увеличением S₂ (свойство 3) на Δв₂ = у₁/у₂ * Δв₁ = = 4/3. Тогда новые запасы ресурсов составят: ;

2.4. Выпуск дополнительной продукции.

Пусть имеется возможность выпуска третьей продукции, причем а₁₃ = 3, а₂₃ = 2, а₃₃ = 4, а₄₃ = 1, с₃ = 3. Ответим на вопросы: дает ли это прибыль? Какой должна быть цена на Р₃, чтобы производство оставалось рентабельным?

По свойству 4 Δ = а₁₂у₁ + а₂₃у₂ + а₃₃у₃ + а₄₃у₄ – 3 = = 3*4/4 + 2*3/5 + 4*0 + 1*0 – 3 = 0,6 > 0, следовательно, производство дополнительной продукции невыгодно. Цена должна быть: 3*4/4 + 2*3/5 + 4*0 + 1*0 – с < 0, не менее 3,6 руб.

2.5. Прирост прибыли при изменении стоимости продукции.

Пусть стоимость первой продукции увеличиться 3 рубля, тогда прибыль изменится на ΔF_max = Δс₁х₁ = 6*5 = 30 руб.

Пусть стоимость второй продукции увеличиться 2 рубля, тогда прибыль изменится на ΔF_max = Δс₂х₂ = 4*2 = 8 руб.