4. Методи обчислення площ на планах землеустрою.

Існують такі методи визначення площ на плані землеустрою:

1. аналітичний

2. графічний

3. механічний

4.1 Аналітичний метод обчислення площ

Аналітичний метод обчислення площ земельних угідь є єдиним з найбільш точним оскільки на його результати впливають помилки польових вимірів та за рахунок округлення. Як правило ці помилки незначні. За допомогою аналітичного методу площі можуть обчислюватись:

1. по лінійним і кутовим величинам геометричних фігур

2. по координатах.

При обчисленні площі трикутника використовують наступні формули:

1. Р =

2. 2P = cbsin

3. P = S= (формула Герона)

4. 2Р =

5. 2Р = (Хс-Х_A)(У_А-Ув) - (Х_А-Хв)(Ус-У_А)

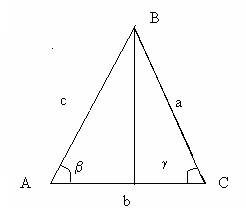
Задача 4 Обчислити площу трикутника, якщо відомо:

1. сторона в та висота до неї h;

2. 2 сторони в та а та кут  між ними;

3. с

   Назва точок	Кути	Довжини ліній	Координати
   			Х	У
   А	310241 4511		4610.31	7810.36
   		421.97
   В	8605413211		4883.17	8132.24
   		249.84
   С	6104014311		4684.16	8283.28
   		478.65
   А

   торона в та кути  і  при ній;

4. всі сторони трикутника;

5. координати точок вершин трикутника

.позначення	Числові величини	позначення	Числові величини	позначення	Числові величини	позначення	Числові величини	позначення	Числові величини
	310241 4511		6104014311	a	249.84	b	478.65	Хс-ХA	73.85
sin	0.521196	sin	0.880300	b	478.65	b2	229105.82	УА-Ув	-321.88
c	421.97	a	249.84	c	421.97		310241 4511	(Хс-ХA)  (УА-Ув)	-23770.84
h	219.59	b	478.65	S	575.23	ctg	1.637460	ХА-Хв	-272.86
b	478.65	2P	105271.52	Sa	325.39		6104014311	Ус-УА	472.92
Pм2	52634.50	Pм2	52635.76	Sb	96.58	ctg	0.538926	(ХА-Хв)  (Ус-УА)	-129040.95
Рга	5.26	Рга	5.26	Sc	153.26	2	105268.93	2 Pм2	105270.11
				Pм2	52635.76	Pм2	52634.46	Pм2	52635.06
				Рга	5.26	Рга	5.26	Рга	5.26

При обчисленні площі інших геометричних фігур використовують такі формули:

Трапеція

1. Р =

2. .Р =

3. .Р =

Паралелограм

Прямокутник

Р = а в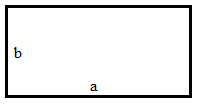

Р

Чотирикутник

омб

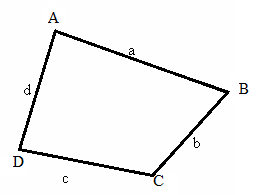
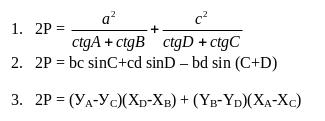
Р = а в

Багатокутник

2Р = Х_К(У_К+1-У_К-1) = У_К(Х_К-1-Х_К+1)

2Р = Х_К*У_(К+1) -Х_К*У_(К-1) = У_К*Х_(К-1) -У_К*Х_(К+1)

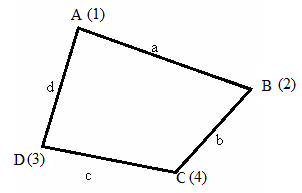
З

Знаходимо площу чотирикутника за формулою:

2Р = (У_А-У_С)(Х_D-X_B) + (Y_B-Y_D)(X_A-X_C)

адача 5 Обчислити площу чотирикутника, якщо відомі координати точок вершин цієї фігури

	Х	У
1	5341,4	2018,5
2	5867,9	2371,2
3	5906,2	2925,3
4	5097,2	2632,2

Позначення	Числові величини	Позначення	Числові величини
У1-У3	-906,8	У2-У4	-261
Х4-Х2	-770,7	Х1-Х3	-546,8
(У1-У3)*( Х4-Х2)	698870,76	(У2-У4)*( Х1-Х3)	147412,8
2Р	= 846283,56	Р= 42,3 га
Р	= 423141,78

Вихідні дані для задачі 5

Варіант	т.1	т.2	т.3	т.4	Варіант	т.1	т.2	т.3	т.4
	Х У	Х У	Х У	Х У		Х У	Х У	Х У	Х У
1	2521.36 6212.25	5680.32 6225.23	8820.56 7256.21	4086,34 9089,16	16	2582.54 6208.56	5703.51 6216.58	8649.62 7358.49	4833,04 9722,14
2	2526.54 6245.98	5642.21 6226.45	8765.23 7358.16	4281,65 9654,94	17	2548.58 6159.24	5845.61 6235.55	8945.62 7394.53	4820,30 9870,43
3	2519.49 6211.51	5694.24 6245.12	8456.94 7588.10	4257,05 9781,90	18	2593.17 6274.64	5713.50 6225.16	8762.54 7984.32	4675,21 9847,26
4	2526.51 6202.35	5632.28 6226.56	8649.62 7358.49	4872,65 9078,84	19	2548.64 6255.23	5712.65 6545.62	8844.26 7354.91	4284,64 9127,19
5	2542.21 6243.25	5679.23 6225.87	8945.62 7394.53	4252,78 9929,51	20	2568.54 6180.30	5658.61 6626.41	8945.62 7394.53	4880,21 9186,04
6	2565.21 6289.37	5684.56 6286.94	8762.54 7984.32	4227,05 9008,68	21	2543.27 6200.65	5690.26 6256.31	8762.54 7984.32	4335,76 9029,66
7	2578.34 6246.45	5599.54 6294.51	8844.26 7354.91	4557,25 9644,67	22	2528.51 6251.32	5651.46 6246.38	8844.26 7354.91	4572,99 9997,03
8	2596.21 6210.36	5635.86 6283.93	8764.94 7251.03	4288,86 9920,39	23	2504.61 6254.65	5689.17 6255.36	8764.94 7251.03	4639,85 9270,80
9	2542.21 6244.65	5662.51 6300.25	8961.50 7549.51	4989,33 9618,84	24	2580.10 6203.56	5657.32 6228.90	8961.50 7549.51	4960,09 9673,30
10	2564.65 6219.26	5688.56 6282.65	8861.92 7591.80	4946,20 9317,03	25	2531.02 6255.56	5712.34 6315.85	8461.92 7691.80	4789,20 9265,10
11	2524.89 6099.21	5634.59 6284.61	8864.83 7498.67	4202,55 9347,77	26	2582.54 6208.56	5690.26 6256.31	8762.54 7984.32	4335,76 9029,66
12	2574.25 6165.26	5611.29 6264.35	8912.20 7542.66	4519,82 9463,59	27	2528.51 6251.32	5611.29 6264.35	8844.26 7354.91	4572,99 9997,03
13	2595.49 6158.51	5642.68 6233.58	8820.51 7256.21	4942,24 9606,73	28	2504.61 6254.65	5684.56 6286.94	8764.94 7251.03	4639,85 9270,80
14	2547.24 6179.52	5667.39 6209.81	8765.24 7358.16	4265,55 9657,22	29	2580.10 6203.56	5657.32 6228.90	8456.94 7588.10	4960,09 9673,30
15	2537.64 6200.31	5699.32 6354.94	8456.92 7588.10	4208,52 9786,37	30	2531.02 6255.56	5712.34 6315.85	8461.92 7691.80	4872,65 9078,84

Задача 6 Обчислити площу багатокутника, якщо відомі координати точок вершин цього багатокутника

№ точок	Х	У
1	5395,5	2058,8
2	5922,1	2394,5
3	5954,5	2963,4
4	5143,4	2688,5
5	4844,5	2886,5
6	4161,5	2557,7
7	4345,3	1663,8
8	4769,8	2048,5

2Р = 2476342

Рм² = 1238171

Р_га = 123,82

Вихідні дані для задачі 6

№ варіанту	1	2	3	4	5	6	7	8
1	5395,5 2058,8	5922,1 2394,5	5950,5 2969,4	5143,4 2688,5	4844,5 2886,5	4144,5 2572,7	4341,3 1663,8	4767,8 2070,5
2	5394,5 2051,8	5919,1 2388,5	5958,5 2968,4	5144,4 2681,5	4823,5 2858,5	4135,5 2543,7	4344,3 1663,8	4764,8 2038,5
3	5399,5 2052,8	5926,1 2395,5	5957,5 2967,4	5140,4 2680,5	4861,5 2870,5	4161,5 2538,7	4340,3 1663,8	4760,8 2052,5
4	5393,5 2054,8	5927,1 2391,5	5957,5 2966,4	5142,4 2683,5	4844,5 2886,5	4172,5 2553,7	4341,3 1661,8	4769,8 2027,5
5	5391,5 2050,8	5922,1 2394,5	5955,5 2965,4	5144,4 2688,5	4842,5 2881,5	4175,5 2540,7	4342,3 1662,8	4761,8 2097,5
6	5399,5 2050,8	5919,1 2388,5	5954,7 2964,1	5143,4 2688,5	4846,5 2889,5	4144,5 2572,7	4344,3 1664,8	4762,8 2061,5
7	5391,5 2051,8	5926,1 2395,5	5956,4 2965,8	5144,4 2681,5	4842,5 2885,5	4135,5 2543,7	4345,3 1664,8	4763,8 2045,5
8	5392,5 2052,8	5927,1 2391,5	5952,1 2962,3	5140,4 2680,5	4841,5 2887,5	4161,5 2538,7	4340,3 1668,8	4764,8 2033,5
9	5393,5 2053,8	5919,1 2388,5	5955,6 2968,8	5142,4 2683,5	4841,5 2880,5	4172,5 2553,7	4347,3 1665,8	4765,8 2048,5
10	5394,5 2053,8	5926,1 2395,5	5953,3 2969,1	5144,4 2688,5	4841,5 2883,5	4175,5 2540,7	4345,3 1663,8	4766,8 2041,5
11	5395,5 2055,8	5927,1 2391,5	5957,5 2967,4	5183,4 2681,5	4842,5 2888,5	4172,5 2553,7	4345,3 1664,8	4769,8 2042,5
12	5393,5 2056,8	5922,1 2394,5	5957,5 2966,4	5142,4 2668,5	4843,5 2889,5	4175,5 2540,7	4344,3 1660,8	4767,8 2043,5
13	5391,5 2058,8	5919,1 2388,5	5955,5 2965,4	5140,4 2681,5	4848,5 2884,5	4144,5 2572,7	4341,3 1668,8	4769,8 2044,5
14	5392,5 2058,8	5926,4 2395,6	5954,7 2964,1	5143,4 2682,5	4843,5 2887,5	4135,5 2543,7	4345,3 1663,8	4770,8 2047,5
15	5392,5 2057,8	5927,1 2391,6	5956,4 2965,8	5143,2 2688,5	4844,5 2889,5	4161,5 2538,7	4341,3 1663,8	4771,8 2049,5
16	5395,5 2058,8	5919,0 2388,4	5952,1 2962,3	5143,4 2688,0	4844,5 2883,5	4172,5 2553,7	4344,3 1663,8	4772,8 2045,5
17	5395,5 2058,8	5926,7 2395,5	5955,6 2968,8	5143,0 2688,2	4847,5 2882,5	4175,5 2540,7	4340,3 1663,8	4763,8 2042,5
18	5396,5 2052,8	5927,3 2391,8	5953,3 2969,1	5143,4 2688,5	4823,5 2858,5	4175,5 2540,7	4341,3 1661,8	4754,8 2034,5
19	5399,5 2059,8	5922,2 2394,3	5957,5 2967,4	5144,4 2681,5	4861,5 2870,5	4172,5 2553,7	4342,3 1662,8	4771,8 2023,5
20	5394,5 2052,8	5919,4 2388,3	5957,5 2966,4	5140,4 2680,5	4844,5 2886,5	4175,5 2540,7	4344,3 1664,8	4789,8 2046,5
21	5395,5 2051,8	5926,5 2395,4	5955,5 2965,4	5142,4 2683,5	4842,5 2881,5	4144,5 2572,7	4345,3 1664,8	4763,8 2042,5
22	5398,5 2057,8	5927,9 2391,4	5954,7 2964,1	5144,4 2688,5	4846,5 2889,5	4135,5 2543,7	4340,3 1668,8	4766,8 2043,5
23	5397,5 2055,8	5917,6 2388,1	5956,4 2965,8	5143,4 2688,5	4842,5 2885,5	4161,5 2538,7	4347,3 1665,8	4769,8 2042,5
24	5399,5 2056,8	5929,1 2392,5	5952,1 2962,3	5144,4 2681,5	4840,5 2887,5	4172,5 2553,7	4345,3 1660,2	4762,8 2045,5
25	5388,5 2049,8	5928,1 2394,5	5955,6 2968,8	5140,4 2680,5	4843,5 2880,5	4175,5 2540,7	4333,3 1670,8	4765,8 2043,5
26	5395,5 2051,8	5926,5 2395,4	5955,5 2965,4	5142,4 2683,5	4842,5 2881,5	4144,5 2572,7	4345,3 1664,8	4763,8 2042,5
27	5399,5 2059,8	5922,2 2394,3	5957,5 2967,4	5144,4 2688,5	4846,5 2889,5	4135,5 2543,7	4340,3 1668,8	4766,8 2043,5
28	5397,5 2055,8	5917,6 2388,1	5956,4 2965,8	5140,4 2681,5	4848,5 2884,5	4144,5 2572,7	4347,3 1665,8	4769,8 2042,5
29	5391,5 2051,8	5926,1 2395,5	5956,4 2965,8	5144,4 2681,5	4840,5 2887,5	4172,5 2553,7	4345,3 1660,2	4762,8 2045,5
30	5388,5 2049,8	5928,1 2394,5	5955,6 2968,8	5140,4 2680,5	4841,5 2880,5	4172,5 2553,7	4347,3 1665,8	4765,8 2048,5