
- •Земельний фонд України станом на 01.01.2013
- •IV. Проект землеустрою. Зміст та стадії створення. Недоліки в землекористуванні.
- •1. Планово-картографічний матеріал при землевпорядкуванні та вимоги до нього, його корегування.
- •2. Врахування деформації плану при визначенні координат точок, довжин ліній та площ фігур.
- •Практична робота №1
- •3. Обчислення координат, довжин ліній та кутів - 2 год.
- •Пряма геодезична задача
- •Обернена геодезична задача
- •Обчислення координат точок перетину двох прямих Задача 2 з твердих точок а і в проведені прямі лінії під дирекцiйними кутами а-к в-к
- •Обчислення елементів кривої
- •4. Методи обчислення площ на планах землеустрою.
- •4.1 Аналітичний метод обчислення площ
- •Графічний метод
- •4.3 Обчислення площ механічним методом
- •Порядок визначення площі на плані землеустрою
- •Проектування земельних ділянок.
- •6.1 Методи проектування земельних ділянок
- •6.2 Проектування земельних ділянок заданої площі.
- •Вихідні дані задачі 12
- •Варіанти для задачі 15
- •Варіанти задачі 16
- •Проектування смуги землі паралельними ломаними лініями.
- •Обчислення виконують в такій послідовності:
- •6.4 Проектування дорізки площ
- •Методом послідовного наближення спроектуємо трапецію з площею р2, прийнявши за основу лінію ae.
- •В першому наближенні проведемо лінію s1 паралельно основі ае. Графічно визначимо довжину лінії s1
- •6.5 Виправлення меж, що складаються з коротких ліній.
- •6.6 Проектування ділянок в межах кварталу.
- •Використана література:
З
Проектування
виконується графічним методом за
допомогою трапеції в наступній
послідовності: З’єднуємо
вершину А з вершиною Е прямою лінією,
з’явиться багатокутник Р1=7733
м2
Обчислюємо
площу Р2
яку треба дорізати до площі Р1,
щоб одержати проектну площу Р. Р2=Р-Р1 По
формулі h1=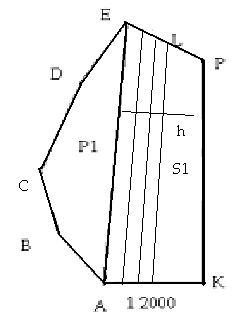
Методом послідовного наближення спроектуємо трапецію з площею р2, прийнявши за основу лінію ae.
В першому наближенні проведемо лінію s1 паралельно основі ае. Графічно визначимо довжину лінії s1
![]() визначаємо висоту цієї трапеції.
Ділимо висоту на 2 відкладаємо на
перпендикулярі h.
визначаємо висоту цієї трапеції.
Ділимо висоту на 2 відкладаємо на
перпендикулярі h.
3.2
в
другому наближенні через кінець відрізка
h/2 проводимо лінію S2
паралельно лінії АЕ і графічно визначаємо
лінію S2.
Визначаємо h2=![]() i
i
![]() .
Відкладаємо
на перпендикулярі h.
.
Відкладаємо
на перпендикулярі h.
3.3
В
третьому наближенні через вершину
відрізка
проводимо лінію S3
паралельну лінії АЕ. Визначаємо графічно
довжину лінії S3,
обчислюємо висоту h3=![]() та
та
![]() половину цієї висоти. Наближення
проводять до тих пір, доки площі Рn
Рn-1
будуть відповідати графічній точності.
половину цієї висоти. Наближення
проводять до тих пір, доки площі Рn
Рn-1
будуть відповідати графічній точності.
4. На проведеному перпендикулярі h відкладаємо відрізок hn (з останнього наближення h3) та проводимо лінію ML паралельно лінії АЕ.
5. Графічно визначаємо довжину лінії ML, EL i AM.
Позначення
Числові величини
Р
Р1
Р2
2Р2
АЕ
LM
EL
AM
-
Налбиж.
Довжина ліній
S
h
h/2
I
II
III
6.5 Виправлення меж, що складаються з коротких ліній.
Задача 20. Межа землекористування між лініями 10-11 та 17-18 складена з 6 коротких ліній, які потрібно замінити 2-ма лініями за умови, що площа землекористування не змінюється.
З адачу
вирішуємо графічним методом за допомогою
трикутників в такій послідовності:
адачу
вирішуємо графічним методом за допомогою
трикутників в такій послідовності:
На лінії 17-18 обираємо створну точку К і з’єтнуєтоїї з 11 точкою прямою лінією. Графічно визначаємо довжину лінії 11-К. = d =357м.
З
кожної вершини ломаної межі проводимо перпендикуляри на лінію 11-К . Утворився ряд простих геометричних фігур. ( трикутників, трапецій). Обчислюємо графічним методом їх площі
Контроль: сума h1+h2+h3+…..=11-K
№ трикутника |
фігура |
а |
в |
h |
Рм2 |
Р га |
1 |
Трикутник |
49 |
|
22 |
539 |
0.05 |
2 |
Трапеція |
49 |
29 |
53 |
2067 |
0.21 |
3 |
Трапеція |
29 |
66 |
41 |
1947.5 |
0.19 |
4 |
Трапеція |
66 |
53 |
49 |
2915.5 |
0.29 |
5 |
Трапеція |
53 |
121 |
42 |
3654 |
0.37 |
6 |
Трапеція |
121 |
38 |
131 |
10414.5 |
1.04 |
7 |
Трикутник |
38 |
|
19 |
361 |
0.04 |
|
|
|
|
357 |
21898.5 |
2.19 |
Визначаємо висоту (h) трикутника, площа якого дорівнює загальній площі утвореної фігури
 =122,7м.
=122,7м.З створеної точки К будуємо перпендикуляр до лінії 11-К і відкладаємо висоту h. Через кінець цієї висоти проводимо допоміжну лінію паралельну лінії 11-К.
Продовжимо лінію 18-17 до перетину з отриманою лінією і там утвориться точки N. З’єднаємо точку N з точкою 11. Одержимо трикутник КN11, площа якого дорівнює площі загальній площі.
Слід звернути увагу, що точку N ми можемо обирати де завгодно на паралельній лінії .
Г
Р
21898.5
2Р
23797
h
122.7
S
357
d
320.00
Задача № 21
Межа землекористування між лініями 10-11 та 17-18 кладена з 6-ти коротких ліній, які потрібно замінити 2-ма лініями за умови, що площа землекористувача на змінюється.
Задачу вирішуємо аналітичним методом в такій послідовності.

-
Точка
Х
У
11
601.0
302.0
12
783.3
327.3
13
653.7
377.3
14
684.6
562.6
15
609.8
693.2
16
772.0
773.1
17
643.7
927.8
18
350.5
991.0
1. Вирішуємо ОГЗ 17-18
позначення |
1 1.18 |
Т.К |
11 |
2 Т.17 |
Т.11 |
N |
|
У |
927.8 |
302. |
870,0 |
У |
991.0 |
959.3 |
302,0 |
У |
-63.2 |
-651.3 |
+568,0 |
Х |
643.7 |
601.0 |
911,7 |
Х |
350.5 |
497.4 |
601,0 |
Х |
+293.2 |
+103.7 |
+310,7 |
tg |
-0.21555 |
6.280617 |
1,858130 |
r |
120101 |
80о5712 |
61о1916 |
|
3470501 |
279о0248 |
61о1916 |
sin |
-0.21076 |
-0,987584 |
0,877323 |
cos |
+0.97754 |
0,157239 |
0,479900 |
S |
299.87 |
659,51 |
647,43 |
S |
299.93 |
659,50 |
647,42 |
S сер. |
299.90 |
659,50 |
647,42 |
2. На лінії 17-18 обираємо створну точку К і обчислюємо її координати
Точки |
|
d |
Х |
У |
Х |
У |
18 |
|
|
|
|
350,5 |
991,0 |
|
3470501 |
150,3 |
+146,9 |
-31,7 |
|
|
К |
|
|
+1 |
|
497,4 |
959,3 |
|
3470501 |
149,6 |
146,2 |
-31,5 |
|
|
17 |
|
|
|
|
643,7 |
927,8 |
|
|
пр. |
+293,1 |
пр.- 63,2 |
|
|
|
|
теор. |
+292,2 |
теор.-63,2 |
|
|
|
|
f |
+0,1 |
f 0 |
|
|
Обчислюємо площу створеної фігури
-
2Р= 260572,97
Р= 130286,48
11601.0
302.0
12
783.3
327.3
13
653.7
377.3
14
684.6
562.6
15
609.8
693.2
16
772.0
773.1
17
643.7
927.8
К
497,4
959,3
Обчислюємо ОГЗ 11-К і визначаємо кут при точці К.
= К-17-К-11 = 3470501 - 279о0248 = 68о4714311
Обчислюємо довжину а – довжину сторони трикутника
![]() =
=
![]() = 423,80
= 423,80
Обчислюємо координати т. N, яка лежить на продовженні ліній 17-18 по формулам:
ХN=ХK + ХN-K
ХN-K = a cos 17-18
YN = YK+YN-K
YN-K = a sin 17-18
позначення |
обчислення |
позначення |
обчислення |
ХK |
497,4 |
YN |
959,3 |
а |
423,80 |
а |
423,80 |
cos 17-18 |
0,977539 |
17-18 |
347о501 |
ХN-K |
+414,28 |
sin 17-18 |
-0,210756 |
ХN |
911,7 |
Y |
-89,32 |
|
|
YN |
870,0 |
Обчислюємо ОГЗ між точкою 11 та т. N та

= 11-R - 11-N = 99о1711711-61о1911611= 37о4310111
= N-11 - N-K = 241о1911611 – 167о501 = 73о2911611
Контроль ++ = 1800 = 37о4310111 + 73о2911611 + 68о4714311 = 180о
