3.2. Способи опису детермінованих сигналів

Для аналізу сигналів необхідно мати їхній опис. За описом (моделлю) порівняно легко отримати параметри сигналу, які істотно впливають на характеристики системи. Залежно від методів аналізу й синтезу систем застосовуються ті або інші способи зображення (опису) сигналів. До основних з них слід віднести:

 словесний опис;

 графічне зображення;

 зображення сигналу у вигляді деякої функції часу х(t);

 зображення сигналу в операторній формі х(р);

 зображення сигналу у вигляді сукупності елементарних сигналів x(ω).

На практиці знаходять застосування багато способів опису. Найбільш широко використовуються словесний, графічний і сукупність функцій частоти. При словесному описі сигналу перелічуються всі його параметри. Словесний опис є неформалізованим, громіздким, неоднозначним.

При графічному описі сигнал зображується у вигляді часових форм, діаграм, графіків. Графічний опис відрізняється точністю й дає можливість точно відображати часову залежність сигналів і їх елементів. Однак він є неформалізованим, відрізняється громіздкістю під час описання складних сигналів.

Формалізованими зображеннями сигналу є такий його опис, який дає можливість перетворювати за формулами й отримувати основниі параметри, які визначають властивості системи. Такими описами є математичні моделі сигналу у вигляді функції часу х(t), оператора х(p) або сукупності елементарних сигналів як функцій частоти х().

При аналізі й синтезі систем зручно зображати сигнал у вигляді сукупності елементарних сигналів, тому що за реакцією системи на елементарний сигнал можна, користуючись методом суперпозиції, визначити реакцію системи на сигнал у довільній формі.

До елементарних сигналів відносять одиничну функцію, ідеальний одиничний імпульс і синусоїдальні коливання (рис. 3.4, а, б, в).

Одинична функція (рис. 3.4, а) визначається співвідношенням

(3.1)

де 1(t – ) — одинична функція; t — поточний час;  — момент початку дії одиничної функції.

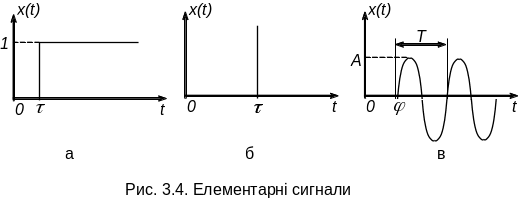
Одинична функція — це часова функція, яка при будь-якому t <  дорівнює нулю, а при будь-якому t ≥  — одиниці. Одинична функція виявляє стрибкоподібні зміни величини х(t) від нуля до одиниці в момент часу t = .

Одиничний імпульс (дельта-функція) (рис. 3.4, б) визначається співвідношеннями:

(3.2)

де (t – ) — дельта-функція; t — поточний час;  — момент дії імпульсу.

Одиничний імпульс — це ідеалізований сигнал, що характеризується нескінченно малою тривалістю, нескінченно великим рівнем, площею, яка дорівнює одиниці.

Синусоїдальне коливання (рис. 3.4, в) визначається співвідношенням

х(t) = Asin (t  ),

де х(t) — синусоїдальна функція часу; А, ,  — амплітуда, кутова частота ( = 2/Т), початкова фаза синусоїдальної функції часу; Т — період змінення функції х(t).

Під час аналізу й синтезу СКК КІВ і їхніх елементів широко використовуються синусоїдальні елементарні сигнали. У зв’язку з цим великий інтерес має зображення сигналу у вигляді сукупності елементарних синусоїдальних сигналів. Так можуть бути зображені як періодичні, так і неперіодичні детерміновані сигнали.