Методичні вказівки

Код Хемінга. Припустимо, що необхідно виправити одиничну помилку у двійковому коді. Такий код складається з бітів, які переносять інформацію і контрольних бітів: всього бітів. Число повинно задовольняти умову . Співвідношення між , , для коду Хемінга наводяться у таблиці 5.1.

Таблиця 5.1

1	0	1		5	2	3		9	5	4		13	9	4
2	0	2		6	3	3		10	6	4		14	10	4
3	1	2		7	4	3		11	7	4		15	11	4
4	1	3		8	4	4		12	8	4		16	11	5

За цими параметрами визначають, які позиції сигналів будуть робочими, а які – контрольними. Практика показала, що номери контрольних бітів зручно вибирати як степені двійки, тобто 1,2,4,8,16,32... Потім обчислюють значення контрольних коефіцієнтів за правилом: сума одиниць на позиціях, які перевіряються, має бути парною. Позиції для перевірки вибирають так. Складають таблицю для ряду натуральних чисел у двійковому коді. Кількість її рядків . Першому рядку відповідає перевірочний коефіцієнт , другому - і так далі.

0001 - 0010 - 0011 - 0100 -

0101 - 0110 - 0111 - 1000 -

1001 - 1010 - 1011 -

У першу перевірку входять коефіцієнти, які містять одиницю у молодшому розряді ( , , , , ...), у другу – в другому розряді ( , , , , ...), у третю – в третьому розряді ( , , , ...) тощо.

Приклад 5.1. Побудувати код Хемінга для виправлення одиничної помилки при передачі комбінації 0101.

Розв’язання. Для нашого випадку . За таблицею 5.1 мінімальна кількість контрольних бітів , при цьому . Контрольні біти будуть знаходитись у позиціях 1,2,4; інформаційні – у позиціях 3,5,6,7: , , , . Для першої перевірки сума буде парною при . З другої перевірки випливає, що . Третя перевірка дасть . Остаточно одержуємо код 0100101.

Припустимо, що під час передачі виникла одинична помилка і було прийнято 0100111. Для знаходження позиції помилки виконуємо ті ж перевірки на парність, що й при кодуванні. Перша перевірка проходить, тому у молодший розряд позиції помилки записуємо 0. Друга і третя перевірки і не проходять, тому у відповідні біти позиції помилки записуємо 1. Звідси номер помилкової позиції .

Групові коди зручно задавати за допомогою породжуючих матриць, кількість рядків яких , а кількість стовпців - . Найчастіше така матриця має вигляд

,

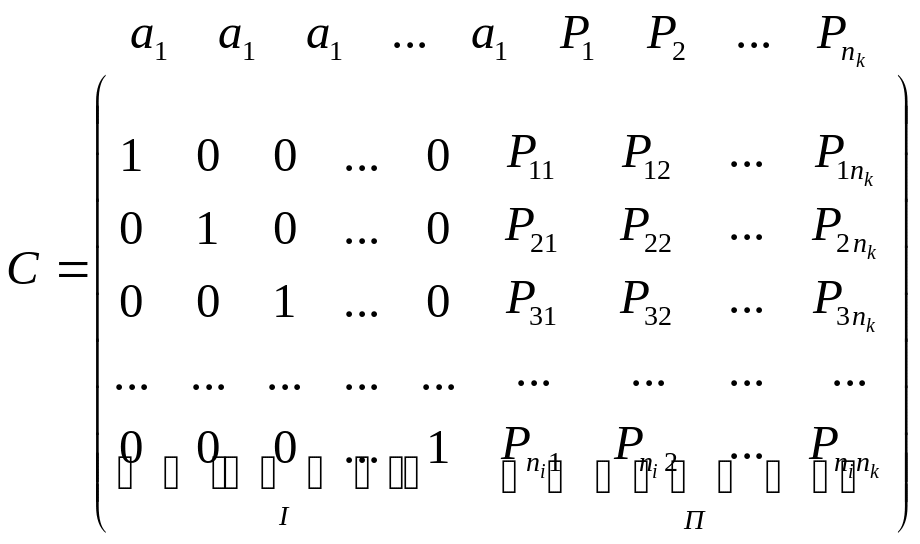де - інформаційна частина, - перевірочна частина. Алгоритм одержання перевірочних бітів за відомою інформаційною частиною коду може бути записаний так:

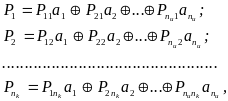
або

Для тестування наявності помилки у прийнятому сигналі обчислюється вектор

, .

Якщо він є нульовим, то помилки немає. Інакше будують допоміжну матрицю , де - одинична матриця порядку . Номер того стовпця матриці , який збігається з вектором , дає позицію помилково прийнятого біта.

Приклад 5.2. Побудувати груповий код за заданою твірною матрицею

для інформаційної комбінації 0101.

Розв’язання. В заданій інформаційній комбінації ненульовими є другий і четвертий біти. Тому для знаходження перевірочного коду додаємо за модулем 2 другий і четвертий рядки матриці П: . Отже 0101101 – коректуючий коду.

Припустимо, що замість нього була прийнята послідовність 0101001. Виконуємо перевірки:

Оскільки вектор не нульовий, то при передачі відбулася помилка. Будуємо матрицю

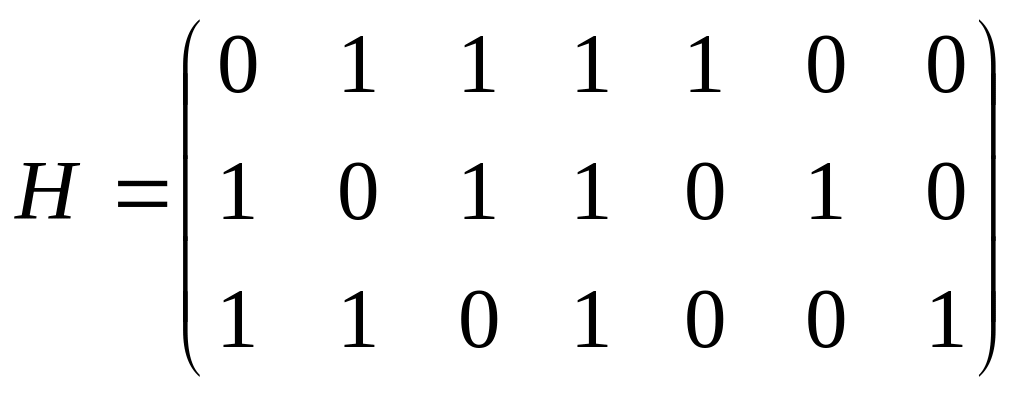
Звідси, оскільки вектор співпадає з п’ятим стовпцем матриці , випливає, що помилково було прийнято саме п’ятий розряд.

Циклічні коди. В них інформаційна послідовність розглядається як масив коефіцієнтів многочлена, наприклад 1101 . Позначимо цей многочлен через . Як коректуючий код вибирається остача від ділення на наперед заданий породжуючий многочлен . Тут — степінь , ділення многочленів виконується в арифметиці за модулем 2.

Приклад 5.3. Побудувати циклічний код, породжений многочленом для інформаційної послідовності 1001.

Розв’язання. Для нашого випадку . Домножуємо на і виконуємо ділення:

10010001011

1011 1010

0100

0000

1000

1011

0110

0000

110

Дописуємо коректуючий код 110 до інформаційної послідовності. Одержуємо 1001110.

Для перевірки правильності прийнятого коду він ділиться на . Якщо остача від ділення дорівнює нулеві, то помилки немає. Інакше підраховується кількість одиниць в остачі . Якщо , де – допустима кількість помилок, які виправляються даним кодом, то прийнята комбінація додається за модулем 2 до одержаної остачі: сума дасть виправлену комбінацію. Інакше циклічно зсовуємо отриману комбінацію вліво і ділимо її на породжуючий многочлен . Виконуємо зсув і ділення доти, поки не задовольниться умова . Після цього додаємо за модулем 2 останню остачу до останнього діленого і здійснюємо циклічний зсув результату вправо на стільки розрядів, скільки було перед цим виконано зсувів вліво.

Приклад 5.4. Показати процес виправлення одиничної помилки в одержаному раніше коді 1001110.

Розв’язання. Нехай помилкова комбінація має вигляд 1000110. Виконуємо її ділення на породжуючий многочлен. Одержуємо остачу 011, для якої . Оскільки для нашого випадку , то потрібно виконати дії:

1. Циклічно зсуваємо 1000110 на один розряд вліво і ділимо ланцюг 0001101 на . Одержуємо остачу 110, для якої .

2. 0001101 0011010, нова остача – 111.

3. 0011010 0110100, нова остача – 101.

4. 0110100 1101000, нова остача – 001. Оскільки тепер 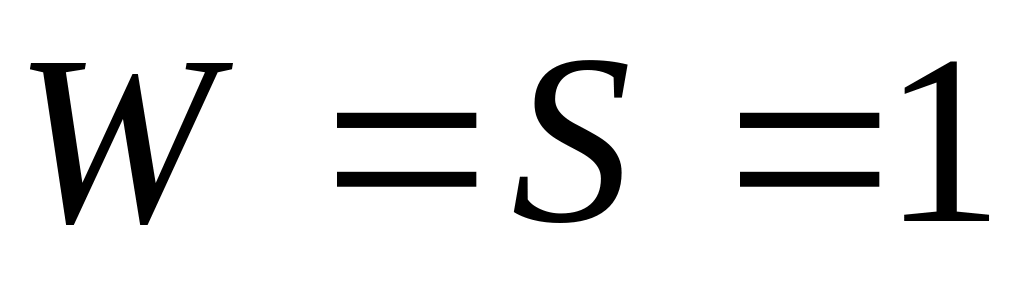, припиняємо зсуви вправо.

Додаємо за модулем 2 останню остачу (001) до останнього діленого (1101000) і виконуємо циклічний зсув результату (1101001) вправо на чотири розряди (тому що перед цим ми чотири рази зсовували прийняту комбінацію вліво). Одержана комбінація 1001110 вже не містить помилок.