Завдання для самостійної роботи

Написати програму-архіватор (непарні варіанти) і програму-розархіватор (парні варіанти), які базуються на методах кодування, перелічених нижче.

1-2. Хаффмена (для текстів, написаних українською мовою), де ймовірності символів задані так:

‘ ‘ - 0.175 ‘о’ – 0.090 ‘е’ – 0.072

‘а’ – 0.062 ‘і’ - 0.062 ‘т’ – 0.053

‘н’ – 0.045 ‘с’ – 0.040 ‘р’ – 0.038

‘в’ – 0.035 ‘л’ – 0.028 ‘к’ – 0.026

‘м’ – 0.025 ‘д’ – 0.023 ‘п’ – 0.021

‘у’ – 0.018 ‘я’ - 0.016 ‘и’ – 0.016

‘з’ – 0.014 ‘б’ - 0.014 ‘г’ – 0.013

‘ч’ – 0.012 ‘й’ – 0.010 ‘х’ – 0.009

‘ж’ – 0.007 ‘ї’ – 0.007 ‘ь’ – 0.007

‘ю’ – 0.006 ‘ш’ – 0.006 ‘ц’ – 0.004

‘щ’ – 0.003 ‘ф’ – 0.002 ‘’’ – 0.002

3-4. Адаптивного методу Хаффмена.

5-6. Арифметичного кодування, (для текстів, написаних українською мовою), де ймовірності обчислюються так само, як і у варіантах 1-2.

7-8. Методом адаптивного арифметичного кодування.

9-10. Методом Лемпеля-Зіва.

11-12. РРМА + адаптивного Хаффмена.

13-14. РРМB + адаптивного Хаффмена.

15-16. РРМC + адаптивного Хаффмена.

17-18. РРМА + адаптивного арифметичного кодування.

19-20. РРМB + адаптивного арифметичного кодування.

21-22. РРМC + адаптивного арифметичного кодування.

23-24. Лемпеля-Зіва + адаптивного Хаффмена.

25-26. Лемпеля-Зіва + адаптивного арифметичного кодування.

Лабораторна робота № 3 Розпізнавання бінарних образів Література: [2,3,4,8,11].

Мета роботи: оволодіти основними методами теорії розпізнавання образів і навчитись застосовувати їх до розв’язування конкретних прикладних задач.

Зміст роботи:

1. Запрограмувати один з методів розпізнавання

2. Порівняти його якість з іншими методами

Методичні вказівки

Використання вектора ознак. При застосуванні цього способу для об’єкта розпізнавання обчислюють його числові характеристики (ознаки). Вибираючи характеристик, одержуємо – вимірний вектор, який називається вектором ознак. Єдиного алгоритму обчислення ознак не існує і в кожному конкретному випадку слід вибирати свої характеристики. Основна вимога при цьому, щоб ознаки добре розрізняли об’єкти і були інваріантними до невеликих деформацій образів. Прикладами таких характеристик можуть бути: розміри об’єкта, яскравість його різних частин, кривизна контура, моментні характеристики, геометротопологічні ознаки тощо. Розпізнавання за вектором ознак є ефективним у випадку аналізу друкованих чи рукописних символів та подібних до них об’єктів. Робота ідентифікуючих систем при використанні вектора ознак складається з двох етапів: навчання системи і безпосередньо розпізнавання. Під час навчання налагоджуються внутрішні параметри системи – вектори еталонів , , де – кількість різних класів об’єктів, що розпізнаються. На цьому етапі системі подаються на вхід представники об’єктів різних класів і для кожного представника вказується, до якого класу він належить. Система обчислює вектор ознак для цього представника, а потім здійснює корекцію відповідного еталону за формулою: , де – параметр налагодження. Під час розпізнавання системі подається на вхід об’єкт для аналізу. Після обчислення його ознак система порівнює вектор з еталонами , . Клас об’єктів, еталон якого мінімізує , вважається розпізнаним.

Граматичні методи розпізнавання. Їх зручно використовувати для ідентифікації рукописних символів під час написання. Фріманом було запропоновано побудувати напрямки написання цифрами від 0 до 7:

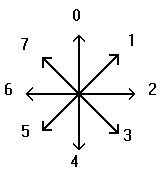
1,1,1,0, 7,6,5,5, 4,4,4,4, 3,2,2,1

Після завершення написання символу одержуємо вектор кодів, належність якого до деякого класу еталонів зручно перевіряти відповідною граматикою. Зокрема, для символу ‘е’ ця граматика має вигляд

Розпізнавання ліній і кіл методом Хоуга. Розпізнавання ліній зводиться до знаходження відповідних пар параметрів рівняння прямої . Якщо зображення має розміри , то , . Розіб’ємо проміжок на рівних частин, – на рівних частин. Одержимо комірок можливих пар . Їм у методі Хоуга відповідає матриця розміру . На початку роботи алгоритму заповнюємо її нулями. Далі скануємо усі точки зображення. Якщо деяка точка є зафарбованою, збільшуємо на одиницю всі комірки матриці , які задовольняють умову . Для цього перебираємо значень , а за ними знаходимо , ідентифікуючи всі такі комірки. Після сканування в тих комірках матриці , які відповідають реально існуючим на зображенні лініям, будуть знаходитись великі числа, а в усіх інших – малі. Описаний метод цілком підходить для ідентифікації кіл. Пошук у цьому випадку здійснюється у 3-вимірному просторі параметрів , які визначають координати центра і радіус кола.