Завдання для самостійної роботи

На відрізку задана функція . Необхідно:

• рівномірно розбити відрізок вузлами, обчислити відліки функції у вибраних точках, намалювати графік функції;

• обчислити коефіцієнти Фур’є , ;

• обчислити перетворення Фур’є , намалювати графік.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

17. .

18. .

19. .

20. .

21. .

22. .

23. .

24. .

25. .

26. .

Лабораторна робота №2

Алгоритми стиснення даних

Література [5,6,12,13].

Мета роботи: Програмно реалізувати основні алгоритми стиснення даних і порівняти результати їх роботи для різних типів вхідних файлів

Зміст роботи:

1 Написати і відладити програму-архіватор яка реалізує один з методів стиснення даних а також відповідну програму-розархіватор

2 Протестувати якість стиснення на різних типах вхідних файлів

Методичні вказівки

Кодування Хаффмена Нехай вхідний потік складається з символів, що належать до множини . Припускаємо, що для кожного символу відома ймовірність його появи  причому >0 Сформулюємо алгоритм покроково

1. Вибираємо з множини два символи і  які мають найменші ймовірності.

2. Ставимо у відповідність символу що має більшу ймовірність біт 0 а іншому – біт 1.

3. Об’єднуємо у множині А символи і в одну групу ймовірність якої дорівнює ( )  Кількість символів у множині А при цьому зменшиться на одиницю.

4. Повторюємо кроки 1-3 доти поки множина А не звузиться до одного символу

Результат роботи цього алгоритму зручно зобразити у вигляді бінарного дерева у вузлах якого розташовані символи (або групи символів) множини  а на гілках записуються кодуючі біти

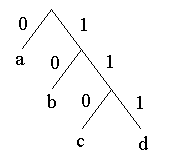
Приклад нехай у вхідному потоці зустрічаються символи ’а’ ’в’ ’с’ ’d’ з імовірностями відповідно 1/2, 1/4, 1/8, 1/8 Тоді побудоване дерево матиме вигляд, зображений на рис. 1.

Рис.1

За код символу візьмемо значення бітів на гілках дерева які треба пройти від кореня щоб потрапити на цей символ ’а’-0 ’в’-10 ’с’-110 ‘d’-111 Отже, для вхідної послідовності авсаваdа одержиться результуючий код 01011001001110 Його довжина дорівнює 14 бітів що на два біти менше ніж звичайне кодування (по два біти на символ).

Адаптивне кодування Хаффмена Для практичної реалізації кодування Хаффмена необхідна апріорна інформація про ймовірності символів. Якщо ж ці ймовірності наперед невідомі, то потрібно застосовувати адаптивне кодування. В цій модифікації методу використовується цілочисельний масив розміром 256 елементів, в якому кожна комірка містить кількість входжень у потік символу з кодом . На початку роботи алгоритму в усі комірки записуються одиниці. Далі виконуємо такі кроки:

1. За лічильниками будуємо бінарне дерево для кодування символів.

2. Читаємо символ з вхідного потоку і записуємо в архівний файл його код.

3. Збільшуємо в масиві на одиницю комірку, яка відповідає прочитаному символу.

4. Продовжуємо кроки 1-3 доти, поки вхідний потік не буде вичерпано.

При розархівації даних масив спочатку заповнюється одиницями, а далі виконуємо такі дії:

1. За лічильниками будуємо бінарне дерево і формуємо коди для кожного можливого символу.

2. Читаємо біти з архівного файла доти, поки не одержимо повністю код деякого символу.

3. Записуємо розкодований символ у результуючий файл і у масиві збільшуємо на одиницю комірку, яка відповідає цьому символу.

4. Виконуємо кроки 1-3 доти, поки архівний файл не буде оброблено повністю.

Арифметичне кодування. В алгоритмі використовуються змінні і , які визначають відповідно ліву і праву межу інтервалу, з яким ми працюємо. На початку роботи алгоритму покладемо . Далі виконуємо кроки:

1. Розбиваємо інтервал на 256 частин згідно з імовір-ностями символів: .

2. Вибираємо ту частину, яка відповідає прочитаному з вхідного потоку символу. Одержуємо нові межі.

3. Якщо , то записуємо в архівний файл 0 і переобчислюємо . Якщо ж , то записуємо в архівний файл 1 і встановлюємо , .

4. Повторюємо кроки 1-3 доти, поки числа і не розмістяться по різні боки від .

5. Поки і , переобчислюємо , .

6. Повторюємо кроки 1-5 доти, поки усі символи з вхідного потоку не будуть оброблені.

При розархівації покладемо спочатку . Далі виконуємо такі дії:

1. Розбиваємо інтервал на 256 частин відповідно до ймовірностей символів: … .

2. Читаємо з архівного файла поточний біт. Якщо він дорівнює 0, то переобчислюємо , інакше .

3. Якщо для деякого символу з кодом справджуються нерівності і , то записуємо цей символ у результуючий файл, присвоюємо і переходимо до пункту 1 цього алгоритму. Інакше – до пункту 2 .

4. Повторюємо кроки 1-3 доти, поки усі символи не будуть розкодовані.

Зауважимо, що:

1. У архівний файл треба заносити довжину вхідного потоку і кількість заповнених бітів в останньому байті цього файла.

2. При декодуванні архівного файла може виникнути ситуація, коли всі біти вичерпано, а ще не всі символи ідентифіковані. Тоді у результуючий файл треба записувати ті символи, інтервали яких містять число 0.5.

3. Алгоритм можна пришвидшити, якщо замість дійсних чисел з інтервалу перейти до цілих чисел з інтервалу , виконавши перемасштабування.

4. Аналогічно як адаптивне кодування Хаффмена, формулюється алгоритм адаптивного арифметичного кодування.

PPM методи обчислення ймовірностей. Для подаль-шого опису алгоритму введемо такі позначення :

– кількість входжень контексту у оброблений вхідний потік;

– кількість різних символів, які слідували після цього контексту (нехай ці символи утворюють множину );

– кількість появи після цього контексту символу з кодом ;

– кількість різних символів, які слідували після цього контексту більше, ніж один раз (нехай ці символи утворюють множину .

Існує три модифікації РРМ-методів, які називаються РРМА, РРМВ, РРМС.

РРМА: ймовірність появи символу обчислюється за формулою . Символи, які не попали у множину мають сумарну імовірність .

РРМВ: , , тобто символ не передбачається, поки він не зустрінеться після контексту двічі.

РРМС: , .

Метод Лемпеля-Зіва. Ідея цього методу полягає в тому, що замість довгих послідовностей символів, які вже зустрічалися у вхідному потоці, записувати в архівний файл посилання на ці послідовності (їх довжину і позицію входження). Найчастіше в архіваторах використовують модифікацію цього алгоритму, при якій входження шукається в останніх прочитаних 4К символів. У цьому випадку для ідентифікації позиції входження необхідно 12 бітів. Для запису довжини послідовності найкраще використовувати 4 біти.