Міністерство освіти України

Чернівецький державний університет імені Юрія Федьковича

ЦИФРОВА ОБРОБКА ІНФОРМАЦІЇ

І РОЗПІЗНАВАННЯ ОБРАЗІВ

МЕТОДИЧНІ ВКАЗІВКИ І ЗАВДАННЯ

ДО ЛАБОРАТОРНИХ РОБІТ

для студентів математичного факультету

спеціальності “Інформатика”

Чернівці

ЧДУ

1999

УДК 681.3.019:621.398

Методичні вказівки і завдання до лабораторних робіт з курсу “Цифрова обробка інформації і розпізнавання образів” /Укл.: Сопронюк Ф.О., Гайдайчук І.В., Фратавчан В.Г. – Чернівці: ЧДУ, 1999. – 36 с.

Друкується за ухвалою редакційно-видавничої ради Чернівецького державного університету імені Юрія Федьковича

Укладачі: Сопронюк Федір Олексійович, доктор фізико-математичних наук, професор (відповідальний за випуск),

Гайдайчук Ігор Васильович, Фратавчан Валерій Григорович, кандидати фізико-математичних наук, асистенти;

Підписано до друку 18.11.99. Формат 60x84/16.

Папір газетний. Друк офсетний. Ум. друк. арк. 1.7. Обл.-вид. арк. 1.8

Зам. 349. Тираж 100 прим.

Друкарня видавництва “Рута” Чернівецького держуніверситету

274012, Чернівці, вул. Коцюбинського, 2

Вступ

Запропоновані методичні вказівки і завдання до лабораторних робіт відповідають курсу “Цифрова обробка інформації і розпізнавання образів”, який читається для студентів п’ятого курсу спеціальності “Інформатика”. Вони покликані допомогти студентам денної та заочної форм навчання більш глибоко засвоїти лекційний матеріал і навчитися застосовувати набуті знання для фільтрації сигналів, кодування та стиснення інформації, розпізнавання конкретних об’єктів.

Структура та зміст даної розробки відповідають вимогам “Освітньо-професійної програми вищої освіти України”. До її складу увійшли такі теми:

• швидке перетворення Фур’є;

• алгоритми стиснення даних;

• розпізнавання бінарних образів;

• використання перетворення Фур’є у розпізнаванні зображень;

• корекція помилок при передачі інформації.

Вказані теми охоплюють майже весь лекційний матеріал, передбачений програмою для вищих навчальних закладів. До кожної з них наведені відповідні теоретичні обгрунтування, деякі ілюструються розв’язаннями типових прикладів, запропоновані варіанти завдань для самостійної роботи і перерахована допоміжна література.

Лабораторна робота № 1 Швидке перетворення Фур’є (шпф) Література [1,2,3,4,8,11].

Мета роботи: Програмно реалізувати швидке дискретне перетворення Фур’є 

Зміст роботи: За заданими відліками функції обчислити коефіцієнти її розкладу в ряд Фур’є, здійснити низькочастотну фільтрацію і зобразити на екрані отриманий сигнал.

Методичні вказівки

Перетворення Фур’є. При розв’язуванні багатьох задач математики та фізики необхідно здійснити розклад періодичної функції з періодом 2 в ряд Фур’є

. (1.1)

Тригонометричний многочлен

збігається в середньоквадратичному до , якщо

, , , (1.2)

Якщо деяка функція задана на інтервалі , то її розклад у ряд Фур’є має такий вигляд:

, (1.3)

де

, , , (1.4)

— основна частота розкладу.

Ряд (1.1) можна записати у вигляді

, (1.5)

де , , або , (1.6)

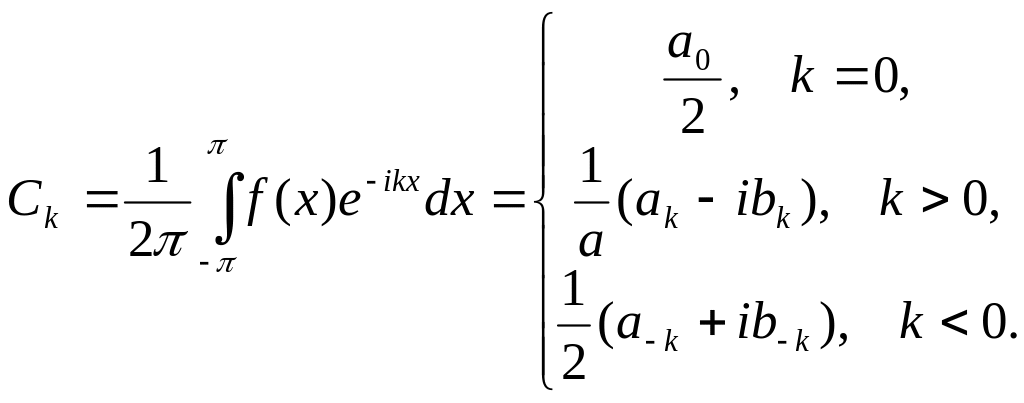де (1.7)

Дискретне перетворення Фур’є. Нехай деяка функція на відрізку відома тільки в дискретній системі точок , , тобто відомі відліки . Позначимо , де - основна частота, . Тоді

, (1.8)

де

, (1.9)

.

Перетворення (1.9) називається дискретним перетворенням Фур’є, при обчисленні якого потрібно використати порядку множень і додавань. У випадку, коли є складеним числом, існує декілька алгоритмів для пришвидшення обчислень. Ці методи отримали назву швидкого перетворення Фур’є. Розглянемо алгоритми, які використовують перехід від одновимірного до двовимірного перетворення Фур’є.

Алгоритм Кулі-Тьюкі. Для його пояснення припустимо, що . Тоді, перепозначивши і , де , , , , запишемо (1.9) у вигляді

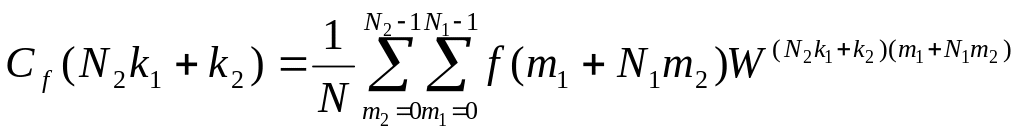. (1.10)

У формулі (1.10) не більше комплексних множень і комплексних додавань.

Остаточно алгоритм Кулі-Тьюкі формулюється так:

1. Записуємо вхідні дані для алгоритму (відліки) у вигляді матриці .

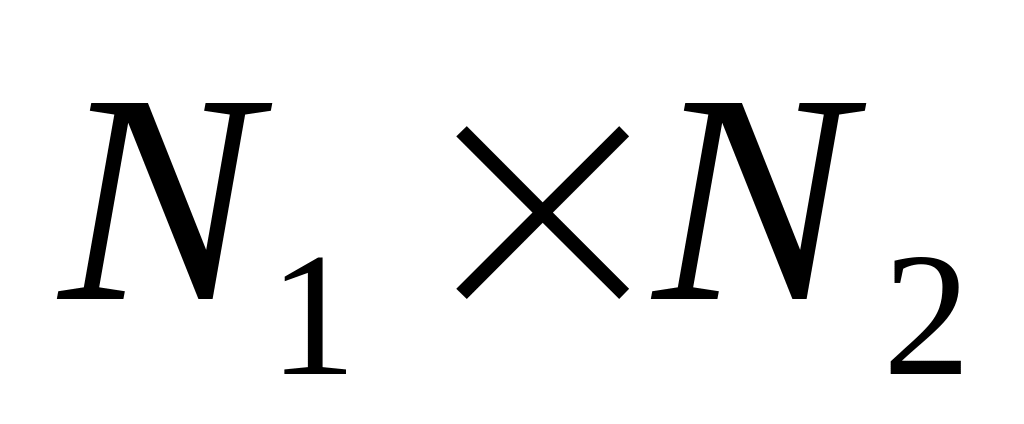2. Виконуємо 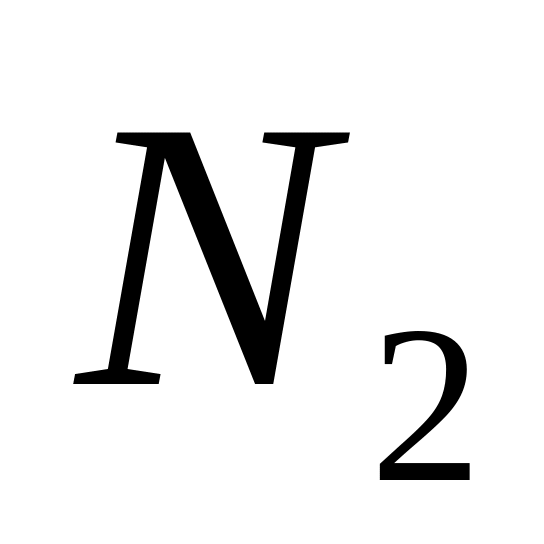-точкове перетворення Фур’є по стовпцях, тобто домножуємо на відповідні 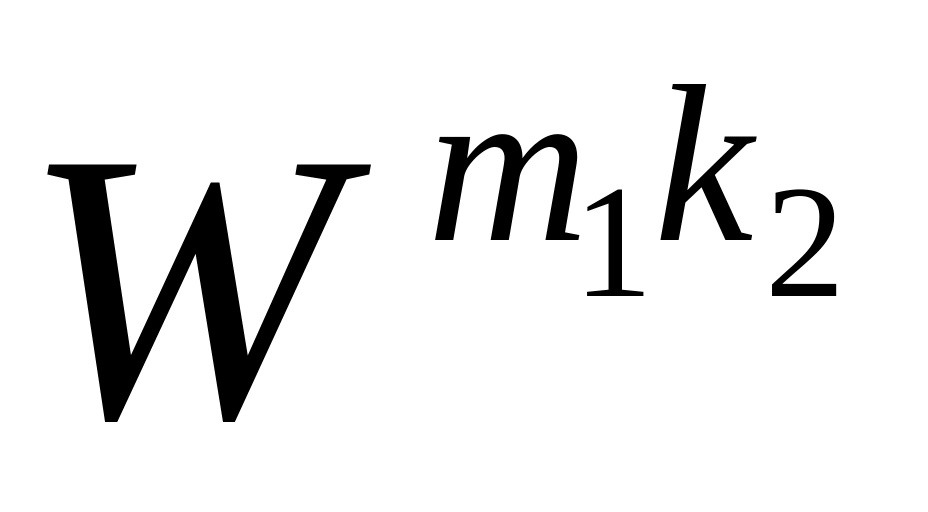. Результати записуємо у цю ж таблицю.

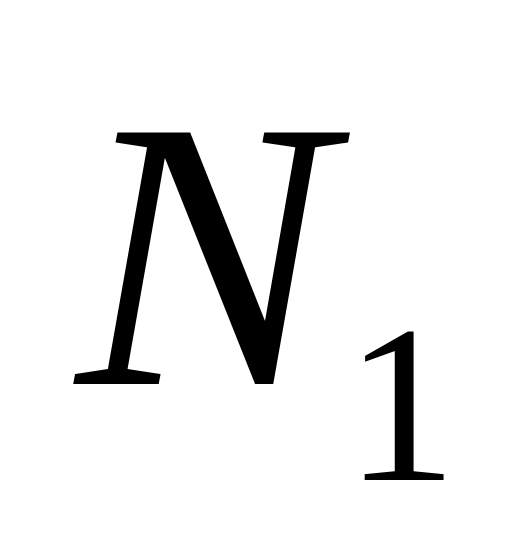3. Обчислюємо -точкове перетворення Фур’є по рядках і записуємо результат у таблицю.

4. Переходимо від таблиці до вектора розміру .

Особливо відмітимо випадок, коли , де -множини натуральних чисел. Тоді алгоритм можна записати рекурсивно. Якщо комплексне множення реалізувати через чотири дійсні множення і два дійсних додавання, то загальна кількість дійсних множень дорівнює , а дійсних додавань — .

Алгоритм Гуда-Томаса. Як і в методі Кулі-Тьюки, припускаємо, що , але додатково вимагатимемо, щоб і були взаємно простими. Індекси у двовимірній таблиці задаються за правилами , . З китайської теореми про лишки випливає існування таких чисел і , що виконується рівність , де . Вихідні індекси у результуючому одновимірному векторі визначаються дещо інакше. Нехай , . Перепишемо ці рівності в еквівалентному вигляді

,

.

Тоді вихідні індекси обчислюються за правилом . У цих нових індексних позначеннях формула (1.9) набуває вигляду

.

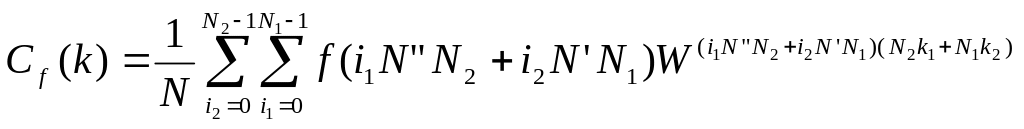Виконаємо множення у показнику степеня. Оскільки порядок елемента дорівнює , то члени з цим показником дорівнюють 1. Тоді описане вище перетворення індексів для елементів вхідної і вихідної таблиць дає

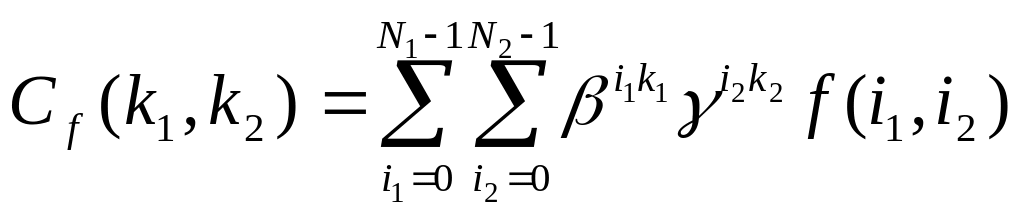, (1.11)

де і . Елементи і є тепер простими коренями з одиниці степенів і , що задають відповідно -точкове і -точкове перетворення Фур’є. Отже, рівняння (1.11) записано тепер у формі двовимірного -точкового перетворення Фур’є. Кількість множень і кількість додавань приблизно дорівнює .

В обох методах перетворення Фур’є по рядках і по стовпцях,

якщо відповідна вимірність задається складеним числом, можна у свою чергу спростити, застосовуючи алгоритм ШПФ.