Пример 4

Менеджер П/ОМ-компании верит, что вероятность благоприятного рынка такая же, как и неблагоприятного; это означает, что каждое состояние природы имеет шанс .50. Теперь мы можем определить EMV для каждого варианта (табл. 3.3).

1. EMV(A1) = (.5)($200 000) + (.5)($ – 180000) = $10000.

2. EMV(A2) = (.5)($100 000) + (.5)($ – 20000) = $40000.

3. EMV(A3) = (.5)($0) + (.5)($0) = $0.

Максимальный EMV – в варианте А2. В соответствии с критерием решения с использованием EMV мы будем строить малый завод.

Таблица 3.3. Варианты выбора

Варианты	Состояния природы
	Благоприятный рынок, $	Неблагоприятный рынок, $
Строить большой завод	200000	-180000
Строить малый завод	100000	- 20000
Ничего не строить	0	0
Вероятности состояний природы	.50	.50

Теперь предположим, что этот менеджер получил предложение от фирмы, занимающейся маркетинговыми исследованиями, по­мочь ему принять решение, строить или не строить завод по производству складских навесов. Исследователи рынка утвержда­ют, что их технический анализ ответит компании определенно, будет ли рынок благоприятным для предложенного продукта. Другими словами, это даст возможность перейти от принятия решения в условиях риска к принятию решения в условиях определенности. Эта информация предохранит компанию от очень дорогой ошибки.

Фирма маркетинговых исследований запрашивает $65000 за информацию. Что порекомендовать компании? Следует ли этому менеджеру нанять фирму, чтобы провести исследование? Даже если информация от этого исследования будет совершенно точ­ной, стоит ли она $65000? Сколько это может стоить?

Хотя на некоторые из этих вопросов трудно ответить, опреде­ление значения такой совершенной информации может быть очень полезно. Это установит верхнюю границу суммы, которую можно потратить на информацию, предлагаемую консультантом по маркетингу.

Какова же концепция ожидаемой ценности совершенной ин­формации?

Если менеджер способен определить, какое состояние приро­ды появится, то затем он сможет определить, какое принять решение. Если менеджер знает, какое принять решение, то отдача от решения увеличивается, потому что эта отдача сейчас означает определенность, а не вероятность. Поскольку эта отдача от реше­ния будет увеличиваться со знанием, какое состояние природы появится, это знание имеет ценность. Поэтому посмотрим, как определить ценность этой информации.

Разницу между отдачей (от решения) в условиях определеннос­ти и отдачей в условиях риска будем называть ожидаемой ценнос­тью совершенной информации. EVPI (Expected Value of Perfect Information).

EVPI = (Ожидаемая ценность в условиях определенности) – (max EMV).

Чтобы найти EVPI, мы должны сначала вычислить ожидаемую ценность в условиях определенности, которая есть ожидаемая или средняя отдача, если мы имеем достоверную информацию перед принятием решения. Чтобы вычислить это значение, мы выбира­ем наилучшую альтернативу для каждого состояния природы и умножаем вызванную ей отдачу на вероятность появления этого состояния природы.

(Ожидаемая ценность в условиях определенности) =

= (Наилучший исход для 1-го состояния природы) х

х (Вероятность 1-го состояния природы) +

+ (Наилучший исход для 2-го состояния природы) х

х (Вероятность 2-го состояния природы) +

+ ... + (Наилучший исход для последнего состояния природы) х

х (Вероятность последнего состояния природы).

Мы используем эти данные и таблицу решения из примера 4 для определения ожидаемой ценности достоверной информации. Делаем это в примере 5.

ПРИМЕР 5

Возвращаясь к табл. 3.3, менеджер компании может вычислить максимальное значение, которое он может платить та информацию, т. е. ожидаемую ценность совершенной информации, или EVPI. Процесс состоит из двух шагов. Прежде всего исчисляется ожидаемая ценность и условиях определенности. Затем, исполь­зуя эту информацию, вычисляем EVPІ. Процедура выглядит следующим образом.

1. Наилучший исход для состояния природы – «благоприятный рынок» – это значит выгодно «строить большой завод» с выплатой $200000. Наилучший исход для состояния природы – «неблагоприятный рынок» – это значит «ничего не строить» с выплатой $0. Ожидаемая отдача в условиях определенности равна

($200000) х (.5) + ($0) х (.5) = $100 000.

Таким образом, если мы имеем совершенную информацию, то будем ожидать (d среднем) $100000, если решение будет повторено многократно.

2. Максимальное ЕMV – ожидаемая отдача в денежном выражении равна $40000, это ожидаемый исход без совершенной информации.

ЕVPІ = (Ожидаемая ценность и условиях определенности) – (max EMV) =

= ($100000) – ($40000) = $60000.

Таким образом, наибольшая сумма, которую компании следует заплатить за совершенную информацию, – это $60000. Вывод базируется на предположении, что вероятность каждого состояния природы – .50.

Метод принятия решений на основе дерева целей. Решения, которые используются в таблицах решений, можно также полу­чить и на дереве целей. Нам следует проанализировать некоторые решения, используя деревья целей. Имея один набор решений и один набор состояний природы, удобнее использовать таблицу решений. Однако многие проблемы включают последовательные решения и состояния природы. Если существуют два или более последовательных решений и позднее решения базируются на исходе предыдущих, подход с использованием деревьев более приемлем.

Дерево целей – это графическое отражение процесса, которое определяет альтернативы решения, состояния природы и их соответствующие вероятности отдачи для каждой комбинации альтернатив и состояний природы.

Хотя мы можем использовать все критерии решений, которые были обсуждены выше, ожидаемая отдача в денежном выражении (ЕMV) – это наиболее используемый и обычно наиболее соответ­ствующий критерий для анализа деревьев целей. Один из первых шагов в этом анализе – это нарисовать дерево целей и определить денежную отдачу всех исходов для конкретной проблемы. Анализ проблемы с использованием дерева целей включает в себя пять шагов.

1. Определить проблему.

2. Структурировать или нарисовать дерево целей.

3. Назначить вероятности к состояниям природы.

4. Оценить отдачу для каждой возможной комбинации альтер­натив и состояний природы.

5. Решить проблему, вычисляя ожидаемую отдачу в денежном выражении (EMV) для каждого узла, состояния природы. Это делается путем движения назад, что значит: начиная справа от дерева и работая назад по узлам решений дерева.

ПРИМЕР 6

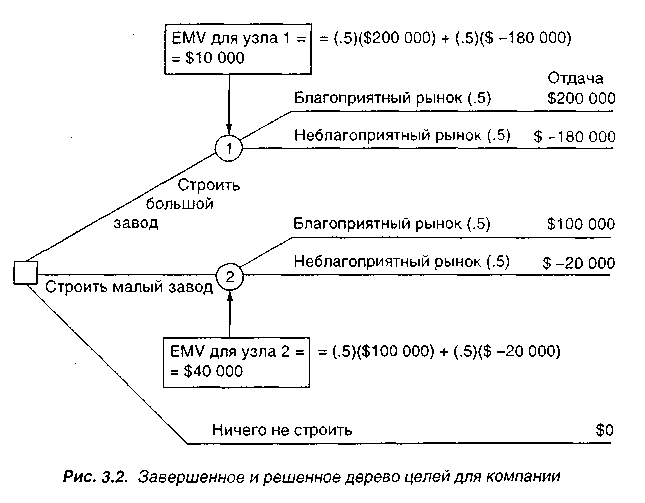
Законченное и решенное дерево целей для компании представлено на рис. 3.2. Заметим, что отдачи помещены в правой части каждой ветви дерева. Вероятности (впервые использованные компанией в примере 4) помешены в скобках рядом с каждым состоянием природы. Ожидаемая отдача в денежном выражении для каждого состояния природы затем вычисляется и помещается в соответствующих узлах.

ЕМУ(1-го узла) = $10000.

Это отражает ветвь от узла решения «строить большой завод». EMV(2-гo узла) = $40000.

Не строить завод или ничего не делать имеет, конечно, отдачу $0. Выбирается ветвь, начинающаяся в узле решения, ведущая к узлу состояния природы с наивысшим EMV. В рассматриваемом случае компанией должен быть построен малый завод.

Более сложное дерево решений. Если нужно выполнить последовательность решений, деревья целей являются более мощ­ным инструментом, чем таблицы решений. Полагаем, что компа­ния имеет два решения, причем следующее решение зависит от исхода первого. Перед принятием решения о строительстве нового завода у компании есть выбор: провести собственное рыночное исследование с затратами $10000. Информация от этого исследо­вания может помочь решить, строить ли большой завод, малый ли или не строить ничего. Компания определила, что такое исследо­вание рынка не обеспечит ее совершенной информацией, но тем не менее немного может помочь.

Новое дерево целей компании представлено на рис. 3.3 приме­ра 7. Если внимательно посмотрим на это более сложное дерево, то заметим, что все возможные исходы и альтернативы включены в их логической последовательности. Это одна из сильных сторон исследования дерева целей в принятии решений. Это подталкива­ет руководителя исследовать все возможные исходы, включая неблагоприятные. Менеджер также побуждается принять решение в логической последовательной манере.

ПРИМЕР 7

Рассматривая дерево на рис. 3.3, мы видим, что первая точка решения – это проводить рыночное исследование за $10000 или нет. Если выбирается решение не делать исследование (нижняя часть дерева) – это может быть строительство либо большого завода, либо малого или не строить завод. Это – вторая точка решения. Рынок будет или благоприятным (вероятность .50), или неблагоприят­ным (также .50). Отдача для каждой из возможных последовательностей обозначе­на в правой стороне. Как видно, нижняя часть дерева компании идентична простому дереву целей на рис. 3.2.

Верхняя часть рис. 3.3 отражает решение проводить рыночное исследование. Узел состояния природы номер 1 имеет две ветви. Будем говорить, что имеется 45-процентный шанс, что результаты исследования укажут благоприятный рынок для складских наве­сов. Заметим, что вероятность .55 будет, если результат будет отрицательным. Остальные вероятности, показанные в скобках рис. 3.3, – все условные вероятности. Например, .78 – вероят­ность благоприятного рынка для навесов, дающая благоприятный результат рыночного исследования. Конечно, можно ожидать найти высокую вероятность благоприятного рынка, когда иссле­дование показало, что рынок был хорошим.

Однако существует также шанс, что 10000-долларовое иссле­дование не даст результат точной или даже надежной информа­ции. Любое рыночное исследование может стать предметом ошиб­ки. В этом случае имеется шанс 22 %, что рынок навесов будет неблагоприятным, хотя результаты исследования будут положи­тельными.

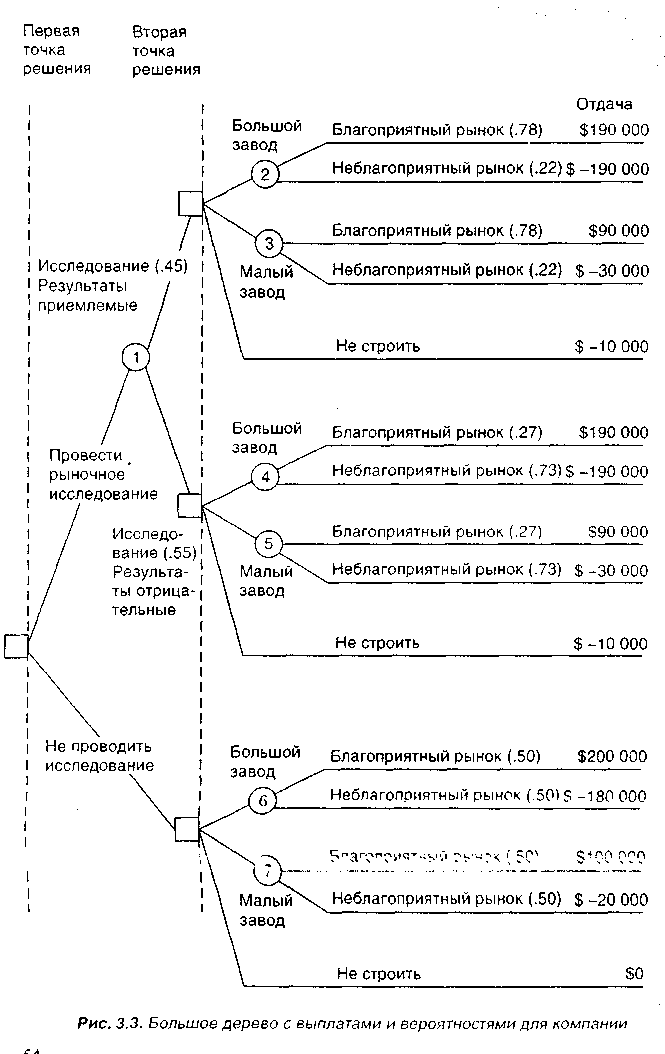
Также заметим, что имеется 27-процентный шанс, что рынок будет благоприятным, хотя исследование компании даст отрица­тельный результат. Вероятность гораздо выше .73, что рынок будет действительно неблагоприятным, когда исследование дало отри­цательный результат.

Наконец, когда мы посмотрим на колонку отдач на рис. 3.3, то увидим, что затраты на 10000-долларовое исследование должны быть вычтены из верхних десяти ветвей. Так, большой завод с благоприятным рынком в нормальных условиях даст $200000 чистой прибыли, но поскольку было проведено рыночное иссле­дование, цифра уменьшается на $10000. При неблагоприятном исходе убыток с $ -180 000 увеличится до $ -190000. Таким же образом проведение исследования и в случае решения «не строить завод» будет сопровождаться выплатой $ -10000.

Определив все вероятности и отдачи, мы можем начать расчет ожидаемых отдач в денежном выражении для каждой ветви.

Начнем с конца или с правой части дерева целей и будем идти в обратную сторону (рис. 3.4). Когда мы закончим, наилучшее решение будет известно.

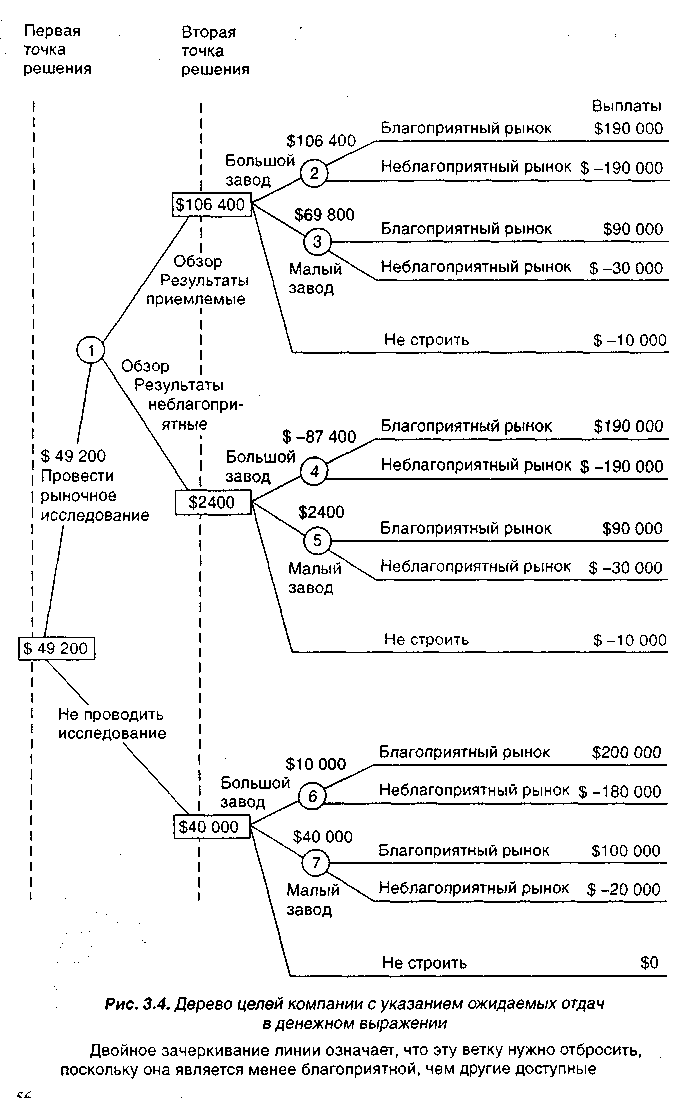
1. Получены благоприятные результаты исследования.

ЕМV (узел 2) = (.78)($190000) + (.22)($ -190000) = $106400.

ЕМV (узел 3) = (.78)($90000) + (.22)(5-30000) = $63800.

EMV в случае решения не строить завод составит $-10000. Если результат исследования благоприятный, следует строить большой завод.

2. Получен отрицательный результат исследования.

ЕМV (узел 4) = (.27)($190000) + (.73)($ -190000) = $ -87400.

ЕМV (узел 5) = (.27)($90000) +(.73)($ -30000) = $2400.

EMV в случае решения не строить завод составит $-10000. Таким образом, если результат исследования неблагоприятный, компания должна строить малый завод с ожидаемым значением отдачи $2000.

3. Продолжая в верхней части дерева двигаться назад, мы вычисляем ожидаемое значение отдачи при проведении рыночно­го исследования.

EMV(узел 1) = (.45)($106400) + (.55)($2400) = $49200.

4. Если рыночное исследование не проводилось

ЕМV(узел 6) = (.50)($200000) + (.50)($ -180000) = $10000.

EМV(узел 7) = (.50)($100000) + (.50)($ -20000) = $40000.

EMV в случае решения не строить завод составит $0. Таким образом, строительство малого завода – наилучший вариант в случае, если не проводится рыночное исследование.

5. Ожидаемая отдача в денежном выражении при проведении рыночного исследования равна $49200 – по отношению к EMV $40000 – без проведения исследования. Отсюда, проведение рыночного исследования дало благоприятный результат и компании следует построить большой завод, но если бы результат был отрицательным, она должна строить малый завод.