Лабораторна робота № 2

Тема. Розв’язання системи лінійних рівнянь методом оберненої матриці

Завдання. Для заданої СЛР визначити головну матрицю системи і знайти матрицю, обернену до головної матриці системи. Здійснити перевірку того, що знайдена матриця дійсно є оберненою. Знайти розв’язок СЛР за методом оберненої матриці. Провести перевірку знайденого розв’язку.

Хід виконання.

1. Записати задану СЛР (варіанти індивідуальних завдань до цієї лабораторної роботи співпадають з варіантами індивідуальних завдань до попередньої лабораторної роботи)

2. Записати СЛР у матричному вигляді

3. Знайти головну та розширену матриці системи

4. Записати значення визначника головної матриці СЛР

5. Знайти доповняльні алгебраїчні мінори головної матриці СЛР і записати обернену до головної матрицю

6. Здійснити перевірку того, що знайдена матриця дійсно є оберненою матрицею до головної матриці СЛР

7. Знайти розв’язок СЛР за допомогою оберненої матиці. Здійснити перевірку знайденого розв’язку

8. Створити програмний додаток розв’язання СЛР методом оберненої матриці

9. Оформити звіт та захистити лабораторну роботу.

Теоретичні питання

1. Квадратна матриця

2. Визначник матриці, його властивості

3. Обернена матриця, приєднана матриця та зв'язок між ними

4. Транспонована матриця, її властивості

5. Доповняльні алгебраїчні мінори

6. Алгоритм знаходження елементів оберненої матриці.

Приклад виконання роботи

Лабораторна робота № 2

Знаходження розв’язків СЛР за допомогою оберненої матриці

Варіант 33.

Задана розширена матриця системи лінійних рівнянь .

Запишемо відповідну СЛР 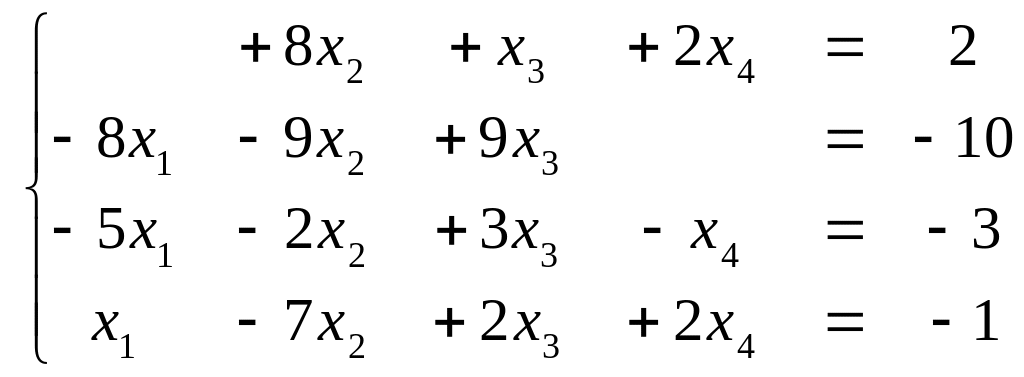(2.1)

Запишемо систему в матричному вигляді:

, (2.2)

або , де – вектор-рядок невідомих ,

– вектор-рядок правих частин, – головна матриця системи.

Визначник головної матриці .

Знайдемо доповняльні (алгебраїчні) мінори. Будь-який доповняльний мінор одержуємо з головного визначника викреслюванням -го рядка і -го стовпця. Тому маємо:

,	,
,	,
,	,
,	,
,	,
,	,
,	,
,	.

Знайдемо матрицю алгебраїчних доповнень.

Алгебраїчне доповнення до елементу матриці системи (2.1) знаходиться за формулою ( ). Матриця алгебраїчних доповнень дорівнює =

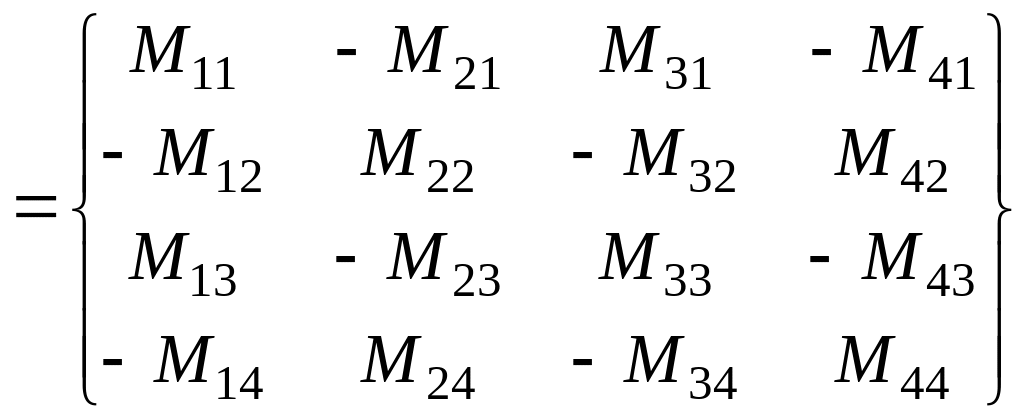Обернена матриця знаходиться за формулою .

Тому

Перевірка знайденої оберненої матриці. Треба здійснити перевірку двох співвідношень і (за означенням оберненої матриці). Нехай , .

Перевірка першого співвідношення.

Знайдемо матрицю Для її елементів маємо

,

,

,

,

,

,

,

,

,

,

,

,

,

,

.

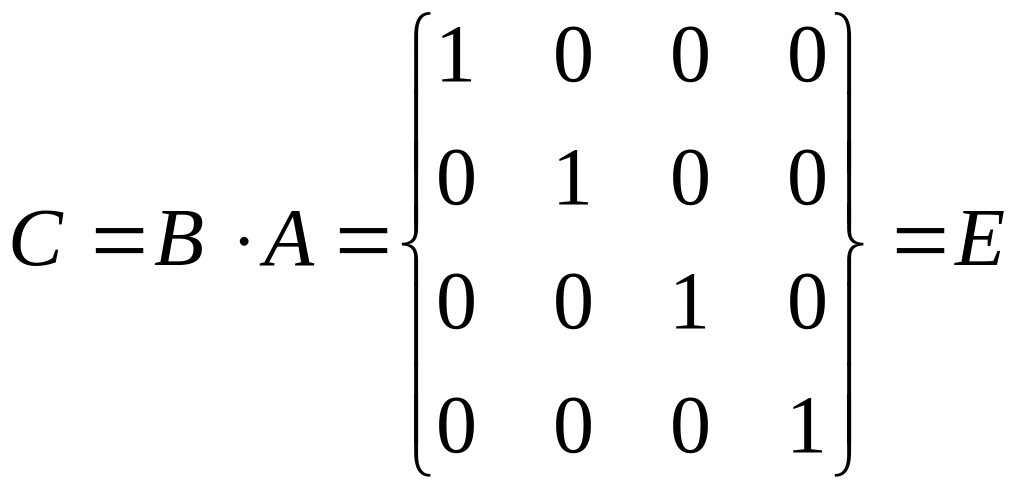Тому і перевірка першого із співвідношень означення оберненої матриці здійснена.

Перевірка другого співвідношення.

Знайдемо матрицю . Для її елементів маємо

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

,

.

Тому і перевірка другого із співвідношень означення оберненої матриці здійснена.

Вектор розв’язку може бути знайдений як добуток оберненої матриці на вектор правих частин

.

Знайдемо кожну з компонент вектора Х:

,

,

,

.

Отже, маємо вектор розв'язку

Перевірку знайденого вектора розв’язку здійснюємо підстановкою знайдених значень невідомих у ліві частини рівнянь системи і одержання значень правих частин.

При маємо:

1) ;

2) ;

3)-5 ;

4)

5) .

Праві частини рівнянь системи дорівнюють лівим частинам. Тому вектор дійсно є розв’язком системи (2.1).

Висновки.

1) Точні розв’язки СЛР з цілими коефіцієнтами є завжди числа дробові. Тому, при знаходженні розв’язку потрібно вести точні (без заокруглень) підрахунки з дробами (у вигляді чисельник/знаменник), щоб одержати точні значення виразів, які ми підраховуємо.

2) Умови застосування методу оберненої матриці до розв’язання СЛР такі ж, як і при застосуванні методу Крамера.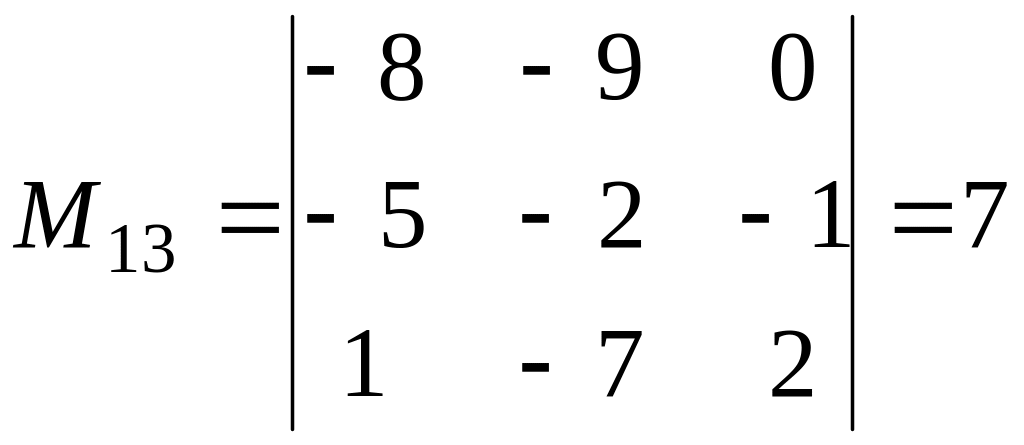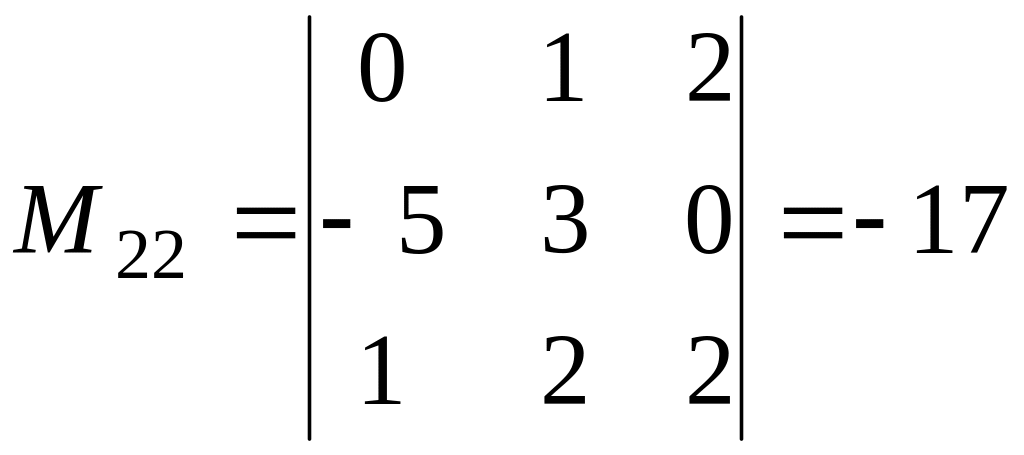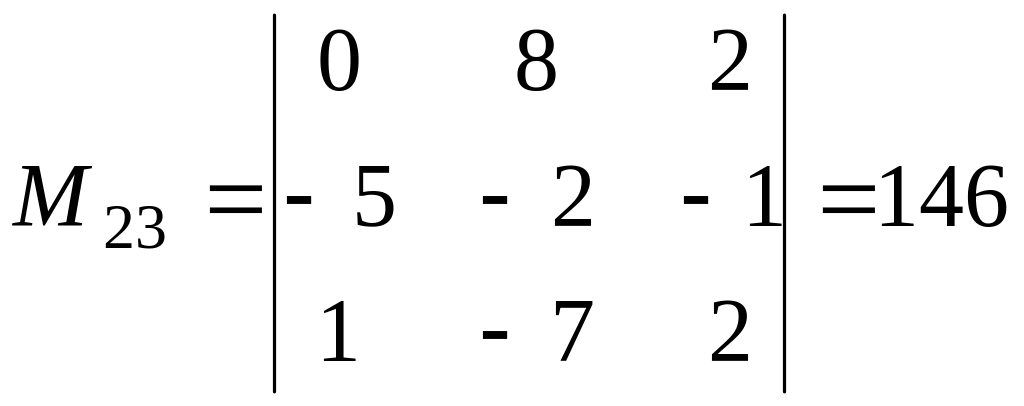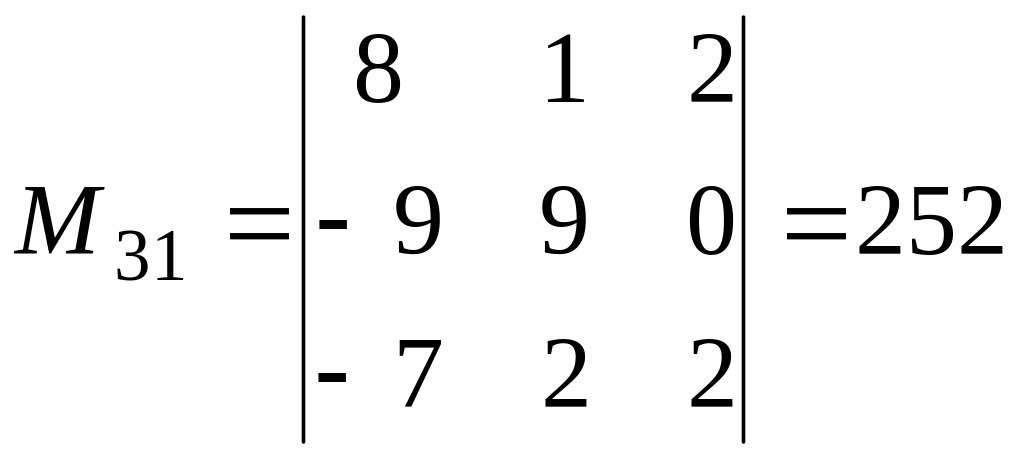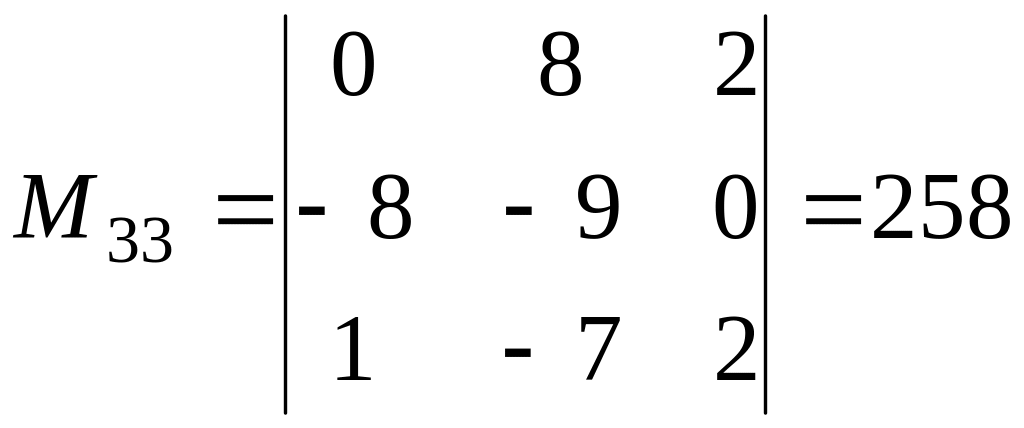