Контрольные вопросы

1. В каких случаях применяют ПИД–регулятор?

2. Представьте принципиальную схему ПИД–регулятора.

3. Каким образом на практике реализуют ПИД–регулятор

4. К какому классу регуляторов относится ПИД–регулятор?

Лабораторная работа № 7

Преобразования структурных схем

Цель работы: Освоить правила преобразования структурных схем .

Преобразование структурных схем используется при получении эквивалентной передаточной функции системы.

Пример. Преобразовать структурную схему, представленную на рис. 7.1, а.

После переноса первого сумматора между звеньями с передаточными функциями W2 и W3, и выполнения связанных с этим изменений в схеме, получим новую структурную схему (см. рис. 7.1, б).

После пошагового выполнения преобразований с параллельно и последовательно соединенными звеньями, а также преобразования схемы со встречно-параллельным соединением звеньев получим эквивалентную структурную схему (см. рис. 7.1, в).

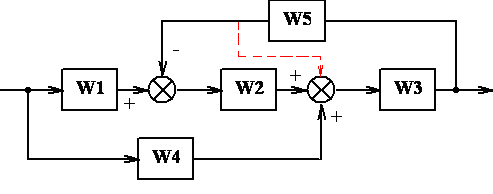
а

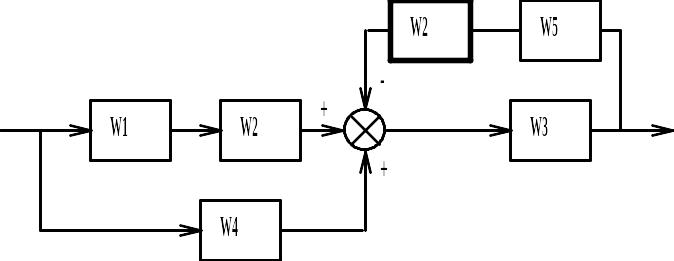
б

в

Рисунок 7.1. Этапы преобразования структурной схемы

Варианты задания

1. Преобразовать структурную схему на рис. 7.2 и привести эквивалентную передаточную функцию при , , W₃ = K₃, W₄ = K₄, W₅ = 1/p, W₆ = K₆, W₇ = K₇.

2. Преобразовать структурную схему на рис. 7.2 и привести эквивалентную передаточную функцию при , W₂ = K₂, , W₄ = K₄, W₅ = 1/p, W₆ = K₆, W₇ = K₇.

3. Преобразовать структурную схему на рис. 7.2 и привести эквивалентную передаточную функцию при , , , , W₅ = K₅, W₆ = 1/p, W₇ = K₇.

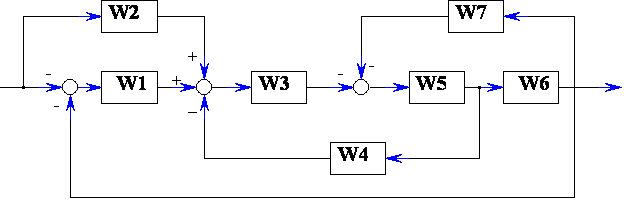
Рисунок 7.2

4. Преобразовать структурную схему на рис. 7.3 и привести эквивалентную передаточную функцию при , , W3 = K3, W4 = K4, .

5. Преобразовать структурную схему на рис. 7.3 и привести эквивалентную передаточную функцию при , W2 = K2, , W4 = K4, .

6. Преобразовать структурную схему на рис. 7.3 и привести эквивалентную передаточную функцию при , , , , .

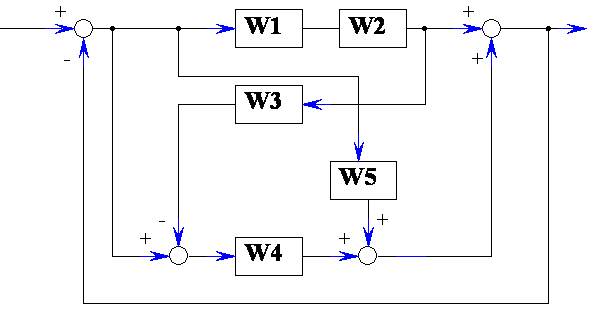
Рисунок 7.3

7. Преобразовать структурную схему на рис. 7.4 и привести эквивалентную передаточную функцию при , W₂ = K₂, , W₄ = K₄.

8. Преобразовать структурную схему на рис. 7.4 и привести эквивалентную передаточную функцию при , , , .

9. Преобразовать структурную схему на рис. 7.4 и привести эквивалентную передаточную функцию при , , W₃ = K₃, W₄ = K₄.

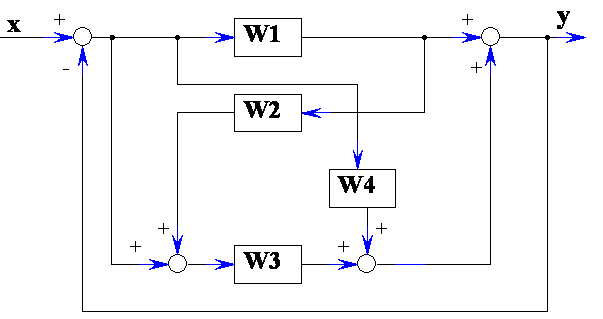
Рисунок 7.4

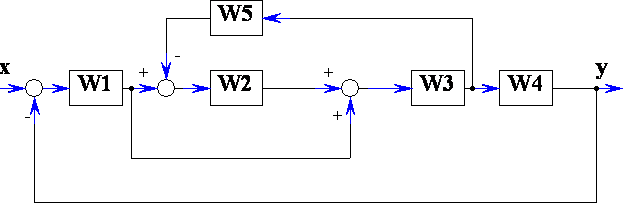
Рисунок 7.5

10. Преобразовать структурную схему на рис. 7.5 и привести эквивалентную передаточную функцию при , W₂ = K₂, , W₄ = K₄, W₅ = K₅.

11. Преобразовать структурную схему на рис. 7.5 и привести эквивалентную передаточную функцию при , W₂ = 1/p, , W₄ = p, W₅ = K₅.

12. Преобразовать структурную схему на рис. 7.5 и привести эквивалентную передаточную функцию при , , , W₄ = K₄, W₅ = K₅.

13. Преобразовать структурную схему на рис. 7.5 и привести эквивалентную передаточную функцию при , W₂ = p, , W₄ = 2, W₅ = 4.

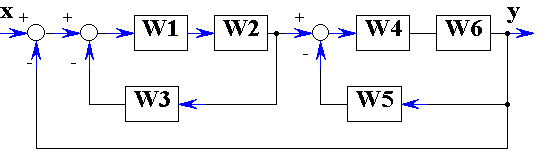
Рисунок 7.6

14. Преобразовать структурную схему на рис. 7.6 и привести эквивалентную передаточную функцию при , W₂ = K₂, W₃ = K₃, , W₅ = K₅, W₆ = K₆.

15. Преобразовать структурную схему на рис. 7.6 и привести эквивалентную передаточную функцию при W₁ = K₁, , W₃ = K₃, , W₅ = K₅, .

16. Преобразовать структурную схему на рис. 7.6 и привести эквивалентную передаточную функцию при , W₂ = K₂, , W₄ = 2, W₅ = 4, .

17. Преобразовать структурную схему на рис. 7.7 и привести эквивалентную передаточную функцию при , W₂ = K₂, W₃ = K₃, , W₅ = K₅, N – нелинейное звено.

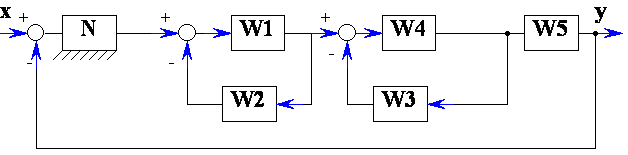
Рисунок 7.7

18. Преобразовать структурную схему на рис. 7.8 и привести эквивалентную передаточную функцию при , W₂ = K₂, W₃ = K₃, , W₅ = K₅, N – нелинейное звено.

19. Преобразовать структурную схему на рис. 7.8 и привести эквивалентную передаточную функцию при , W₂ = K₂, , W₄ = K₄, W₅ = K₅, N – нелинейное звено.

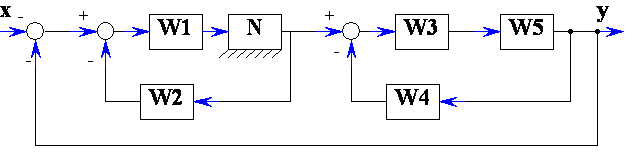
Рисунок 7.8

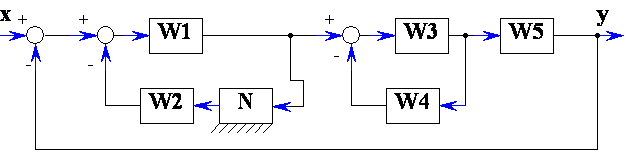
Рисунок 7.9

20. Преобразовать структурную схему на рис. 7.9 и привести эквивалентную передаточную функцию при , W₂ = K₂, W₃ = K₃, , W₅ = K₅, N – нелинейное звено.

21. Преобразовать структурную схему на рис. 7.9 и привести эквивалентную передаточную функцию при , W₂ = K₂, , W₄ = K₄, W₅ = K₅, N – нелинейное звено.

22. Преобразовать структурную схему на рис. 7.9 и привести эквивалентную передаточную функцию при , W₂ = K₂, , W₄ = K₄, W₅ = K₅, N – нелинейное звено.

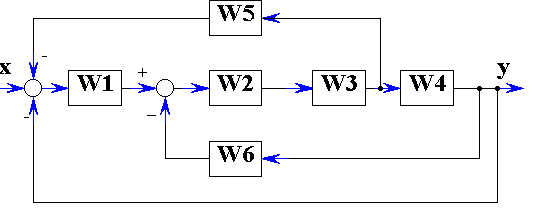
Рисунок 7.10

23. Преобразовать структурную схему на рис. 7.10 и привести эквивалентную передаточную функцию при W₁ = K₁, , W₃ = K₃, , W₅ = K₅, W₆ = K₆.

24. Преобразовать структурную схему на рис. 7.10 и привести эквивалентную передаточную функцию при , W₂ = K₂, W₃ = K₃, , W₅ = K₅, W₆ = K₆.

Рекомендуемая литература

1. Алексеев А.А., Имаев Д., Х., Кузьмин Н.Н., Яковлев В.Б. Теория управления. Учеб. - СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 1999. – 435 с.

2. Теория автоматического управления: Учеб. пособие для вузов /Анхимюк В.Л., Опейко О.Ф., Михеев Н.Н. - Минск: Дизайн ПРО, 2000. - 351 с.

3. Методы классической и современной теории автоматического управления : Учеб.: В 3 т. /ред. Егупов Н.Д., - М.: Изд-во МГТУ, 2000. – 747 с.

4. Теория автоматического управления: Учеб. для вузов /Брюханов В.Н., Косов М.Г.,

Протопопов С.П. и др.,, ред. Соломенцев Ю.М. - М.: Высш. шк., 2000. - 268 с.

5. Бесекерский В.А., Попов Е.П. Теория систем автоматического управления. – М.: Наука. 1975, 318 с.

6. Борцов Ю.А. Математические модели автоматических систем/ ЛЭТИ. – Л., 1981.

7. Зайцев Г.Ф. Теория автоматического управления и регулирования. – М.: Высшая школа, 1988 – 431 с.

8. Иванов А.А. Теория автоматического управления и регулирования/ Недра, 1970.

9. Изерман Р. Цифровые системы управления. – М.: Мир. 1988 .- 216 с.

10. Лукас В.А. Теория автоматического управления. Учеб. М. Недра, 1990. – 416 с.

11. Теория автоматического управления / под. Ред. Воронова А.А. – М.: Высшая школа, 1986 – 538 с.

12. Теория автоматического управления / под ред. Нетушила А.В. – М.: Высшая школа. 1988. – 488 с.

13. Методические указания по применению в учебном процессе диалогового пакета прикладных программ машинного анализа и синтеза систем в среде MASS для студентов электротехнических специальностей. Составители: Е.М.Васильев, Ю.Н. Хижняков, Пермь, 1990.

14. Солодовников В.В., Плотников В.Н., Яковлев А.В. Основы теории и элементы систем автоматического регулирования. – М.: Машиностроение, 1985. – 195 с.

15. Сборник задач по теории автоматического регулирования и управления. 5-е изд. перераб. и доп. / Под ред. В.А. Бесекерского. – М.: Наука, 1978.

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Пермский государственный технический университет

Лысьвенский филиал

Лабораторная работa

по информатике

Тема «»

Выполнил студент ______________________________________________ И.О. Фамилия

^{подпись, дата}

Группа Э-08-1

Направление 150900 «Технология, оборудование и автоматизация машиностроительных производств»»

Преподаватель _________________________________________________ И.О. Фамилия

^{подпись, дата}

Лысьва, 2008

Жесткая обратная связь действует как в установившемся режиме, так и в переходном процессе.

Гибкая обратная связь действует только во время переходного процесса.

Положительной называется обратная связь, которая с увеличением сигнала на выходе элемента передает на его вход воздействие, вызывая при этом последующее увеличение выходного сигнала.

Отрицательной называется обратная связь, которая с увеличением сигнала на выходе элемента передает на его вход воздействие, вызывая при этом уменьшение выходного сигнала.

32