Занятие 14

Неопределенный интеграл

1. Основные определения. 2. Свойства неопределенного интеграла. 3. Способы вычисления неопределенных интегралов

В математике, как правило, для каждого действия над изучаемыми объектами (числами, функциями, векторами и т. п.) определяется и обратное действие: сложение – вычитание, умножение – деление и т. п. Основное действие дифференциального исчисления – дифференцирование, или отыскание производной данной функции. Действие, обратное дифференцированию, – интегрирование, или отыскание такой функции, для которой данная функция является производной.

Функция F (x), определенная на интервале (a, b), называется первообразной для функции f (x) на этом интервале, если для  х (a, b) выполняется равенство

.

Первообразная определяется с точностью до произвольной постоянной С, так как

.

Множество всех первообразных функции f (x) на интервале (a, b) называется неопределенным интегралом от функции f (x) и обозначается

, где F  (x) = f(x).

З

Рис. 14.1

нак называется знаком неопределенного интеграла; х – переменной интегрирования; функция f (x) – подынтегральной функцией, f(x) dx – подынтегральным выражением.

Геометрически неопределенный интеграл представляет семейство кривых y = F(x) + C. Полагая С = С₁, получаем одну кривую, при С = С₂ получаем вторую кривую и т. д. Все кривые этого семейства могут быть получены из одной кривой параллельным сдвигом в направлении оси Oу (рис. 14.1).

Основная задача интегрального исчисления – нахождение первообразной для заданной функции. Эта задача сложнее, чем задача дифференцирования. Оказывается, для всякой непрерывной функции существует первообразная, но эта первообразная не всегда является элементарной функцией. Соответствующие неопределенные интегралы называются неберущимися. Приведем примеры некоторых «неберущихся» интегралов: ; ; ; ; ; ; ; .

Данные интегралы представлены в справочной математической литературе [2].

Общего метода для нахождения первообразных функций не существует!

Интегральное исчисление предлагает несколько целесообразных приемов, с помощью которых мы научимся интегрировать довольно широкий класс наиболее часто встречающихся функций.

Свойства неопределенных интегралов:

1. .

2. Свойство линейности:

, ₁  R, ₂  R.

Замечание: Свойство справедливо для любого конечного числа слагаемых.

3. Свойство инвариантности формул интегрирования: Всякая формула неопределенного интегрирования сохраняет свой вид при подстановке вместо независимой переменной х любой дифференцируемой функции u =  (x), т. е. если , то и , так как dF(u)= .

Таблица производных, дифференциалов, неопределенных интегралов (u = u(x) – дифференцируемая функция; n, a – const)

№ п/п	Производная	Дифференциал du= u dx	Интеграл
1	(un)= nun–1u	d un = nun–1du	n  – 1
2	(eu)= eu u	d eu =eu du
3	(au)= au ln a u	dau =au ln a du
4	(ln u)= u	d ln u = d u
5	(loga u)= u	d loga u = d u
6	(sin u)= cos u  u	d sin u = cos u du
7	(cos u)= – sin u  u	d cos u = – sin u du
8	(tg u) = u	d tg u = d u
9	(ctg u)= u	d ctg u = d u
10	(arcsin u)= u	d arcsin u = d u	= = – arccos u +С
11	(arccos u)= u	d arccos u = – du
12	(arctg u)= u	d arctg u = du	= = – arcctg u +С
13	(arcctg u)= u	d arcctg u =– du

Дополним таблицу основных интегралов выражениями для часто встречающихся неопределенных интегралов.

14. ; 15. ;

16. ; 17. ;

18. ; 19. .

При интегрировании на первых порах встречаются неожиданности. Рассмотрим интегралы: . Интегралы 1) и 2) очень похожи на интегралы 3) и 4), различие состоит в том, что в них вместо ln x проставлен sin x. Однако не берутся в элементарных функциях, а , (проверьте по определению).

Пример 14.1. Вычислите неопределенные интегралы, применив свойство инвариантности формул интегрирования и таблицу интегралов:

1) ; 2) ; 3) ;

4) ; 5) ; 6) ;

7) ; 8) ; 9) ;

10) ; 11) ; 12) ;

13) ; 14) ; 15) ;

16) ; 17) ; 18) .

1) = [обозначим переменную, стоящую под знаком дифференциала tg x = u] = = [по формуле 1 таблицы интегралов] = = [возвращаемся к исходной переменной] = ;

4) = [обозначим ] = = [по формуле 2 таблицы интегралов] = e^u +С =[возвращаемся к исходной переменной] = .

12) = [обозначим ln x = u] = = [по формуле 12 таблицы интегралов] = arctg u + C = arctg (ln х) + C;

Ответы: 2) ; 3) ; 5) ;

6) 2^arcsinx /ln2+C; 7) ln(1+x²)+C; 8) ;

9) ln(arcсos x) + C; 10) sin 3x + C;

11) –cos (x²); 13) ;

14) ; 15) +C;

16) ; 17) ;

18) .

Интегралы можно вычислять, применяя тождественные алгебраические и тригонометрические преобразования подынтегральной функции, свойства линейности и инвариантности.

Пример 14.2. Вычислите неопределенные интегралы, используя свойства, тождественные преобразования подынтегральной функции и таблицу интегралов.

1) ; 2) ; 3) ;

4) ; 5) ; 6) .

1) = = [делим почленно числитель на знаменатель] = = [используем свойства линейности] = =  = [по формулам 1, 4 таблицы интегралов] = =  .

2) = [используем формулу тригонометрии ] = = = = [по формуле 9 таблицы интегралов и свойству 1] = .

Ответы. 3) tg 3x – 3x + C; 4) ;

5) ; 6) ln² 7x + 5x + C.

Часто при вычислении интеграла применить таблицу интегралов сразу не удается и необходимо сделать тождественные преобразования подынтегрального выражения, т. е. и подынтегральной функции, и дифференциала, используя при этом свойства дифференциала. Такой прием интегрирования называется внесением функции под знак дифференциала, он основан на свойстве инвариантности дифференциала. Вспомним определение дифференциала и его основные свойства.

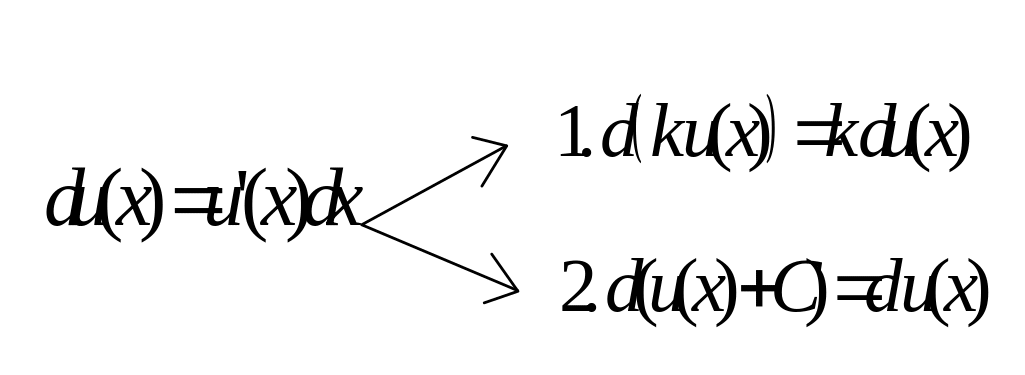
Пример 14.3. Вычислите интегралы, используя свойства дифференциала и прием внесения функции под знак дифференциала. Проведем проверку дифференцированием.

1) ; 2) ; 3) ; 4) ;

5) ; 6) ; 7) ; 8) ;

9) ; 10) ; 11) ;

12) ; 13) ; 14) ;

15) ; 16) .

4) = [так как (х³) =3х² и d(x³)=3x²dx, внесем функцию х² под знак дифференциала: ] = = [по формуле 2 таблицы интегралов] = .

Отметим, что решить задачу помогло нам знание:

• производной функции u(x)=х³;

• формулы вычисления дифференциала ;

• свойства линейности неопределенного интеграла:

;

• табличного интеграла .

Кроме того, догадка – подвести именно х² под знак дифференциала. Н.Н. Лузин писал: «При современном состоянии науки интегрирование, в сущности, есть процесс целесообразно направленных гадании и попыток, для облегчения которых составлена таблица так называемых интегралов»^*.

5) = [представим ] = = [так как (cos x) = – sin x, внeсeм sin x под знак дифференциала: sin x dx = = – d cos x; вынесем знак (–) за знак интеграла] = = [Обозначим cos x = u] = = [по формуле 4 таблицы интегралов] = =  .

6) [так как (ln x)  , вносим под знак dx: .

7) = [(e^2x) = 2e^2x внесем функцию e^2х под знак дифференциала d(e^2x) = e^2x dx] = = .

Ответы: 1) ; 2) ;

3) ; 8) +С; 9) ;

10) ; 11) ; 12) ;

13) ; 14) ; 15) ;

16) .

При вычислении других, более сложных интегралов будем пользоваться справочниками.

Пример 14.4. Используя справочную литературу по математике, найдите интегралы:

1) ; 2) ; 3) ;

4) .

1. = [в справочнике^* находим интеграл вида + С, в нашем случае a = 2, b = 3] = ;

2. = [в справочнике^** находим интеграл ви­да = (a sin bx – b cos bx), в нашем случае a = 2, b = 5] = (2 sin 5x – 5 cos 5x) + С = (2 sin 5x – – 5 cos 5x) + С.

Ответы: 3) ; 4) .

Интегралы вычислить сложнее, чем производные. Чтобы овладеть элементарными методами интегрирования, требуется проделать большое число упражнений.