
- •Исследование и построение графиков функций с помощью производных
- •13.1. Возрастание и убывание функций
- •13.2. Экстремумы функции
- •13.3. Выпуклость и вогнутость графика функции, точки перегиба
- •13.4. Асимптоты кривой
- •13.5. Полное исследование функции и построение графиков
- •13.6. Наибольшее и наименьшее значения функции на отрезке
- •Алгоритм 10 Нахождение наибольшего и наименьшего значений функции на отрезке[a, b]
- •Задания для самостоятельного решения
13.4. Асимптоты кривой
Прямая называется асимптотой кривой, если расстояние между точками линии и прямой стремится к нулю, когда точки кривой неограниченно удаляются от начала координат. Асимптоты бывают вертикальными, наклонными и горизонтальными.
Вертикальная асимптота

Рис. 13.5
Е

Рис. 13.6
сли х0 – точка бесконечного разрыва функции , то –
уравнение вертикальной асимптоты (рис.
13.5). У непрерывных кривых вертикальных
асимптот нет.
–
уравнение вертикальной асимптоты (рис.
13.5). У непрерывных кривых вертикальных
асимптот нет.
Наклонная асимптота
Уравнение
наклонной асимптоты
![]() ,
(k¹0),
где
,
(k¹0),
где
 ,
,
 (рис. 13.6).
(рис. 13.6).
Г

Рис. 13.7
оризонтальная асимптота – частный случай наклонной асимптоты при k = 0; её уравнение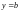 ,
где
,
где
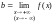 (рис. 13.7).
(рис. 13.7).
Пример
13.4.
Найдем асимптоты графика функции
 и построим схематический чертеж.
и построим схематический чертеж.
 ,
х = 2
– точка разрыва функции.
,
х = 2
– точка разрыва функции.
 При
При
 – 0 числитель ®
5, а знаменатель ®
– 0. Применим условную запись:
– 0 числитель ®
5, а знаменатель ®
– 0. Применим условную запись:
 =
=
 .
.
Аналогично
 .
В точке х = 2
функция терпит бесконечный разрыв,
следовательно, х = 2
– уравнение вертикальной асимптоты.
Находим наклонную асимптоту в виде
;
.
В точке х = 2
функция терпит бесконечный разрыв,
следовательно, х = 2
– уравнение вертикальной асимптоты.
Находим наклонную асимптоту в виде
;

Рис. 13.8
 .
.
Отметим,
что при
 и
и
 получаем k = 1.
получаем k = 1.

 .
.
Уравнение
наклонной асимптоты
 .
Горизонтальных асимптот нет, так как
.
Горизонтальных асимптот нет, так как
 .
Схематический чертеж дан на рис. 13.8.
.
Схематический чертеж дан на рис. 13.8.
13.5. Полное исследование функции и построение графиков
Мы рассмотрели основные элементы поведения функции. Общий план исследования приведен в табл. 13.1.
Алгоритм 9 Полное исследование функций Шаг 1. Устанавливаем общие свойства функции: п. 1. Находим Df и точки разрыва функции. п. 2. Проверяем функцию на четность, нечетность и периодичность. Шаг 2. Находим асимптоты кривой:
а)
вертикальные:
б)
наклонные:
в) горизонтальные (если k = 0).
Шаг
3.
Исследуем функцию на монотонность и
на экстремум
(с
помощью
п. 3.
Находим
и вычисляем критические точки из
уравнения
п. 4. Отмечаем на числовой оси критические точки, принадлежащие Df, и определяем знаки в каждом интервале.
При
п. 5. Определяем экстремумы функции: если при переходе через критическую точку х0 производная меняет знак а) с «–» на «+» – в точке х0 минимум; б) с «+» на «–» – в точке х0 максимум.
Вычисляем
Шаг
4. Исследуем
функцию на выпуклость, вогнутость,
находим точки перегиба (с помощью
п. 6.
Находим
и вычисляем точки, в которых
п. 7. Отмечаем на числовой оси найденные точки, принадлежащие Df, и определяем знаки в каждом интервале:
п. 8. Если при переходе через точку х0 (где или не существует) вторая производная меняет знак, то х0 – точка перегиба. Шаг 5. Составляем таблицу, используя полученные данные исследования. Шаг 6. На основе таблицы строим график функции. |
При проведении частичного исследования функции выполняем следующие пункты алгоритма 9:
1) исследование на монотонность – п. 1, шаг 3 п. 3, 4;
2) исследование на экстремум – п. 1, шаг 3 п. 3, 4, 5;
3) исследование на выпуклость, вогнутость графика функции – п. 1, шаг 4 п. 6, 7;
4) нахождение точек перегиба – п. 1, шаг 4 п. 6, 7, 8;
5) нахождение асимптот графика функции – шаг 2.
Пример
13.5.
Покажите, что функция
 везде возрастает.
везде возрастает.
Пример
13.6.
Покажите, что функция
 убывает в любом интервале, не содержащем
точку
убывает в любом интервале, не содержащем
точку .
.
Пример 13.7. Найдите интервалы монотонности функций
1)
 ; 2)
; 2)
 ; 3)
; 3)
 .
.
Ответы:
1)
 возрастает при хÎ(–¥;
–1) È
(3; ¥);
убывает при хÎ(–1;3);
2)
возрастает при
возрастает при хÎ(–¥;
–1) È
(3; ¥);
убывает при хÎ(–1;3);
2)
возрастает при
 ;
убывает при
;
убывает при
 ;
3)
убывает при
;
3)
убывает при
 ;
возрастает при
;
возрастает при
 .
.
Пример 13.8. Найдите экстремумы функций:
1)
 ; 2)
; 2)
 ; 3)
; 3)
 .
.
Ответы:
1)
 ,
,
 ;
;
2)
 ,
,
 ;
;
3)
 .
.
Пример
13.9.
Найдите
интервалы
выпуклости, вогнутости и точки перегиба
графика функции: 1)
 ;
2)
;
2)
 .
.
Ответы:
1)
интервалы: вогнутости –
 È
(1; ¥),
выпуклости –
È
(1; ¥),
выпуклости –
 ;
;
 –
точки перегиба; 2) интервалы: выпуклости
–
–
точки перегиба; 2) интервалы: выпуклости
–
 ,
вогнутости –
,
вогнутости –
 ;
–
точка перегиба.
;
–
точка перегиба.
Пример 13.10. Найдите асимптоты графика функции и постройте схематический график.
1)
 ,
2)
,
2)
 ;
3)
;
3)
 .
.
Ответы:
1) Асимптоты: x = 2, y = 1 (рис. 13.9) |
2) Асимптоты: x = –1, y = x (рис. 13.10) |
3) Асимптоты: x = 0, y = 2 – x (рис. 13.11) |

Рис. 13.9 Рис. 13.10 Рис. 13.11
Пример 13.11. Проведите полное исследование функций и постройте графики:
1)
 ; 2)
; 2)
 ; 3)
; 3)
 ;
;
4)
 , 5)
, 5)
 .
.
1) Используем алгоритм 9.
Шаг
1:
п. 1.
 .
Функция непрерывна, точек разрыва (и,
следовательно, вертикальных асимптот)
нет.
.
Функция непрерывна, точек разрыва (и,
следовательно, вертикальных асимптот)
нет.
п. 2. Функция четная, поэтому график симметричен относительно оси Оy, непериодическая.
Шаг
2.
Находим наклонные асимптоты кривой в
виде
 ;
;
 –
наклонных асимптот нет;
–
наклонных асимптот нет;
 =
0. Уравнение горизонтальной асимптоты
=
0. Уравнение горизонтальной асимптоты
 .
.
Ш аг
3.
п. 3. Находим интервалы монотонности и
экстремумы функции:
аг
3.
п. 3. Находим интервалы монотонности и
экстремумы функции:
 .
Критические точки находим из уравнения
.
Критические точки находим из уравнения

 .
.
п.
4
возрастает при
 ,
убывает при
,
убывает при
 .
.
п. 5. Так как при переходе через критическую точку меняет знак с «+» на «–», то – точка максимума, f max = f(0) = 1.
Шаг 4. п. 6. Находим интервалы выпуклости, вогнутости графика функции и точки перегиба с помощью второй производной:
 =
= ;
;
 при
при

 .
.
п.
7.

При
 график вогнутый, при
график вогнутый, при –
выпуклый.
–
выпуклый.
п.
8. Точки
–
точки перегиба, так как при переходе
через эти точки вторая производная
меняет знак;
 .
.
Шаг 5. Составляем таблицу, в которую вносим все результаты исследования
x |
|
|
|
0 |
|
|
|
|
+ |
+ |
+ |
0 |
– |
– |
– |
|
+ |
0 |
– |
– |
– |
0 |
+ |
|
возрастает, вогнута |
точка перегиба
|
возрастает, выпукла |
max
|
убывает, выпукла |
точка перегиба
|
убывает, вогнута |
Шаг 6. Получаем график кривой, которая называется кривой Гаусса (рис.13.12) и широко используется в теории вероятностей.

Рис. 13.12
2)
Это тоже кривая Гаусса, которая смещена
по оси 0x
вправо, если
 ,
и влево, если
,
и влево, если
 ,
причем чем больше величина σ,
тем
«шире» кривая Гаусса и меньше ее
максимальное значение (рис. 13.13).
,
причем чем больше величина σ,
тем
«шире» кривая Гаусса и меньше ее
максимальное значение (рис. 13.13).

Рис. 13.13
Ответы:
3

Рис. 13.14

Рис. 13.15
)
 ,
–
уравнение вертикальной асимптоты,
–
уравнение горизонтальной асимптоты
при
;
,
–
уравнение вертикальной асимптоты,
–
уравнение горизонтальной асимптоты
при
;
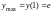 ;
убывает при
;
убывает при
 ;
возрастает при
;
возрастает при
 ;
точек перегиба нет; при
график вогнутый, при
;
точек перегиба нет; при
график вогнутый, при
 –
выпуклый (рис. 13.14).
–
выпуклый (рис. 13.14).
4)
 ,
непрерывна,
–
уравнение горизонтальной асимптоты
при
;
убывает при
;
возрастает при
;
,
непрерывна,
–
уравнение горизонтальной асимптоты
при
;
убывает при
;
возрастает при
;
 ;
при
;
при
 функция вогнута, при
функция вогнута, при
 –
функция выпукла,
–
функция выпукла,
 – точка перегиба,
– точка перегиба,
 (рис. 13.15).
(рис. 13.15).
5

Рис. 13.16
) , непрерывна, асимптот нет; возрастает при хÎ(–¥;0)È(2; ¥); убывает при хÎ(0;2); f max = f (0) = 2, f min =f (2) = – 2; функция вогнута при x>1, функция выпукла при x < 1, x = 1 – точка перегиба, f (1) = 0 (рис. 13.16).
