
Задания для самостоятельного решения
3.1. Решите системы линейных уравнений:
а), в), г) – методом Гаусса;
а), б), в) д), е) – используя формулы Крамера и обратную матрицу.
а)
 ; б)
; б)
![]() ;
в)
;
в)
 ;
;
г)
 ;
д)
;
д)
 ;
е)
;
е)
 .
.
3.2. Решите однородные системы линейных уравнений и постройте вектор, указывающий направление прямой:
а)
![]() ;
б)
;
б)
![]() ;
в)
;
в)
![]() .
.
3.3. Решите неоднородные системы линейных уравнений:
а)
![]() ;
б)
;
б)
 ;
в)
;
в)
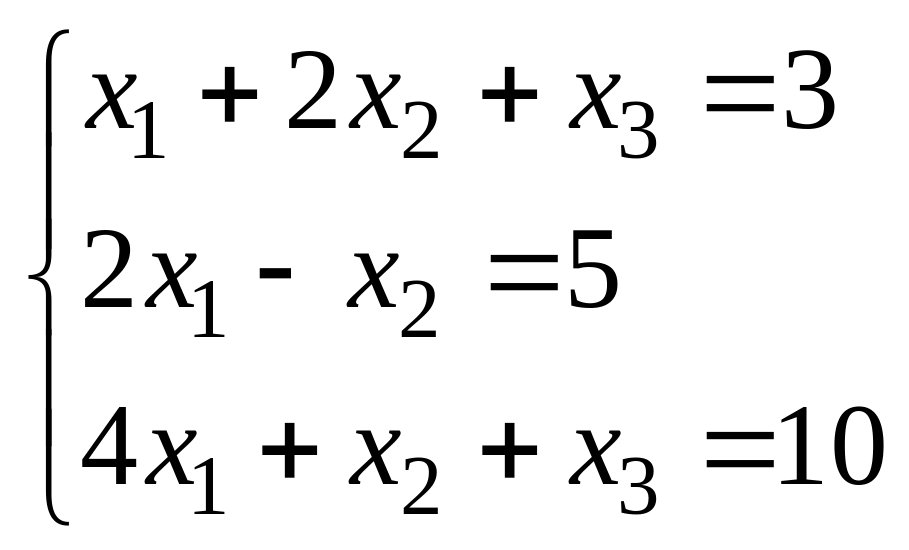 ;
;
г)
 ;
д)
;
д)
![]() .
.
Занятие 4
Элементы теории множеств
1. Основные определения. 2. Способы задания множеств. 3. Операции над множествами, свойства операций
Множество – совокупность вполне различимых объектов одной природы, называемых элементами множества.
Принадлежность элемента а множеству А обозначают а А («а» принадлежит множеству А), если «а» не принадлежит множеству А, то пишут а А.
Множество А называется подмножеством множества В (обозначается А В), если всякий элемент из множества А является элементом В (рис. 4.1). Если А В и А В, то А называется строгим подмножеством (обозначается А В). Множества А и В равны, если их элементы совпадают (или А В и В А).
М
Рис.
4.1

Примеры бесконечных множеств:
числовые: N Z Q R
N – множество натуральных чисел;
– множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I – множество иррациональных чисел;
R – множество действительных чисел.
множества точек на числовой оси, которые представлены в табл. 4.1.
Т а б л и ц а 4.1
№ п/п |
Название |
Обозначение |
Определение |
Изображение |
1 |
Интервал |
(а, в) |
A = {х | а < х < в} |
а в |
2 |
Отрезок |
[а, в] |
A = {х | а х в} |
[/ / / / / / / / /] а в |
3 |
Полуинтервал |
(а, в] [а, в) |
A = {х | а < х в} A = {х | а х < в} |
(/ / / / / / / / /] а в [/ / / / / / / / /) а в |
4 |
Полубесконечный интервал |
(–, в] [а, ) |
A = {х| – < х в} A = {х| а х < } |
/ / / / / / / / / /] в
а |
5 |
– окрестность точки а |
(a – , a + ) |
A = {х| а–<х<а+} |
(/ / / / / / / / / /) a – a a + |
6 |
Бесконечный интервал |
R = (–, ) |
A = {х| – < х < } |
/ |
Способы задания множеств:
Перечислением (списком) своих элементов. Списком можно задавать лишь конечные множества, например А = {a, b, c, d};
Порождающей процедурой, которая описывает способ получения элементов либо других объектов. Например, множество всех целых чисел, являющихся степенями двойки
 ,
n
N,
может быть представлено порождающей
процедурой, заданной двумя правилами:
1) 1
,
n
N,
может быть представлено порождающей
процедурой, заданной двумя правилами:
1) 1
 ;
2) если m
,
то 2m
;
;
2) если m
,
то 2m
;Описанием характеристических свойств, которыми должны обладать его элементы: M = {x / P(x)} или M = {x: P(x)}.
Пример 4.1. Зададим разными способами множество N всех натуральных чисел: 1, 2, 3 …
Так как множество бесконечно, его нельзя задать списком;
Порождающая процедура содержит два правила:
1) 1 N; 2) если n N, то n + 1 N;
Описание характеристического свойства элементов множества N:
N = {x: x – целое положительное число}.
Пример 4.2. Описать множества перечислением элементов:
а) А = {х Z / (х+5)(2х – 1)(х – 1) = 0};
б)
![]() ;
;
в) C
=
![]() .
.
а)
Множество А
– множество решений уравнения (х
+ 5)(2х
– 1)(х
– 1) = = 0,
принадлежащих множеству целых чисел
Z.
Поскольку решениями уравнения являются
числа х1
= – 5, х2
=![]() ,
х3
= 1, но
число
х2
=
Z,
то множество А
= {– 5; 1}.
,
х3
= 1, но
число
х2
=
Z,
то множество А
= {– 5; 1}.
Ответы: б)
B
=
![]() ;
в) C
= {– 2, – 1,
0, 1, 2, 3}
;
в) C
= {– 2, – 1,
0, 1, 2, 3}
Пример 4.3. Описать множества, задав каждое числовым промежутком:
a)
![]() ;
б)
;
б)
![]() ;
;
в)
![]() .
.
М
Рис.
4.2

Для решения неравенства построим схематически график функции у = (х – 1)(х – 2) (рис. 4.2). Очевидно, что (х – 1)(х – 2) < 0 для каждого х из промежутка (1; 2), таким образом, множество А = (1; 2).
Ответы: б) В = [– 2; 2], в) С = (– 1; 5).
Пример 4.4 Изобразить множества на координатной плоскости:
а)
![]() ;
;
б)
![]() ;
;
в)
![]() ;
;
г
Рис.
4.3

![]() .
.
a )
Множество А
– все точки, принадлежащие прямой у
= 2х
– 1
(рис. 4.3).
)
Множество А
– все точки, принадлежащие прямой у
= 2х
– 1
(рис. 4.3).
б) Множество В удовлетворяет одновременно двум неравенствам y x, y x2 (рис. 4.4)
в) Элементами множества С являются точки окружности радиуса R = 2 (рис. 4.5).
г) Элементами множества D являются точки круга радиуса R = 2 (рис. 4.6)

Рис. 4.4 Рис. 4.5 Рис. 4.6
Над множествами можно производить алгебраические операции, которые представлены в табл. 4.2.
Т а б л и ц а 4.2
№ п/п |
Название |
Обозначение |
Определение |
Диаграммы Эйлера–Венна* |
Аналоги для чисел |
1 |
Объединение (сумма) |
А В |
{х | х А В } |
|
a + в |
2 |
Пересечение (произведение) |
А В |
{х | х А х В} |
|
a в |
3 |
Разность |
А \ В |
{х | х А х В} |
|
a – в |
4 |
Дополнение |
Ā = U \ А |
{х | х А } |
|
– |
* Диаграммы Эйлера–Венна – геометрическое представление множеств. Построение диаграммы заключается в изображении прямоугольника, представляющего универсальное множество U, а внутри него – кругов (или каких-либо других замкнутых фигур), представляющих множества.
Замечание. Объединением и пересечением конечного числа множеств А1,…, Аn называются множества соответственно:
![]() ,
,
![]() .
.
П
Рис.
4.7

А С, А С,
А В С, А В С,
В \ А, В \ С
Ответы:

Пример 4.6. Установите соответствие между множествами и диаграммами.
С = В \ А; К = А \ (А В),
М=А\В, L=
А В , D = ![]() ;
;
1) 2) 3) 4)

Ответы: С2; D1; К3; М3.
Пример 4.7. Опишите множество, задав его промежутками.
![]() .
.
Ответ:
![]() .
.
Пример 4.8. Даны множества A={–1; 0; 1; 3} и В = {–3; –1; 0; 1}. Определите множества А В, А В, А \ В, В \ А. Являются ли А и В а) равными, б) равномощными?
Ответы: а) нет, б) да.
А В = {–3; –1; 0; 1; 3}, А В = {–1; 0; 1}, А \ В = {3}, В \ А = {–3}
Пример 4.9.
Приняв отрезок [0, 1] за универсальное
множество U,
найдите и изобразите на числовой оси
дополнения Ā
следующих множеств: а) ![]() ,
б) В
= (1, 2), в)
,
б) В
= (1, 2), в)
![]() .
.
Д ополнением
этого множества до отрезка [0, 1]
является точка х =
0, не входящая
в А,
и промежуток справа от точки
ополнением
этого множества до отрезка [0, 1]
является точка х =
0, не входящая
в А,
и промежуток справа от точки
![]() ,
т. е.
полуинтервал
,
т. е.
полуинтервал
![]() .
Таким образом,
.
Таким образом,
![]() .
Изображаем
.
Изображаем
![]()
Ответы:
б) (0, 1),
в)
![]()
Операции над множествами обладают свойствами, которые приведены в табл. 4.3.
Т а б л и ц а 4.3
1. Коммутативность |
А В = В А (А А= А ) А В = В А (А А= А ) |
2. Ассоциативность |
А (В C) = (А В) C А (В C) = (А В) C |
3. Дистрибутивность |
А (В C) = (А В) (А C) А (В C) = (А В) (А C) |
4. Законы нуля и единицы |
А = А А = А А = |
5. Законы де Моргана |
|
Пример 4.10. Даны множества: А – студенты группы, знающие английский язык; В – студенты группы, знающие немецкий язык; С –студенты группы, знающие французский язык.
Опишем словами,
что означают множества 1) А В,
2) А C,
3) А В C,
4) (А В) C,
5) А В C,
6)
![]() ,
7) А \ В
,
7) А \ В
Ответы:
1) А В –студенты, знающие или английский, или немецкий, или оба этих языка.
2) А C –студенты, знающие и английский и французский, т. е. знающих 2 языка – английский и французский.
3) А В C –студенты, знающие и английский, и немецкий, и французский, т. е. три языка.
4) (А В) C –студенты, знающие или английский с французским, или немецкий с французским, или все три языка, т. е. множество студентов, знающих не менее двух языков (хотя бы два языка), один из которых французский.
5) А В C –студенты, знающие какой-либо один язык из трех, или знающих два языка из трех: английский и немецкий, английский и французский, немецкий и французский, или знающих все три языка, т. е. А В C – множество студентов знающих хотя бы один язык.
6) – студенты, не знающие английского, но знающие немецкий язык.
7) А \ В – студенты, знающие английский язык, причем из числа этих студентов исключены студенты, знающие кроме английского немецкий язык.
Пример 4.11.
Пусть
![]() – подмножества множества R.
Найдите и изобразите на координатной
прямой следующие множества:
– подмножества множества R.
Найдите и изобразите на координатной
прямой следующие множества:
А В,
А В,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
А \ В.
,
А \ В.
О тветы:
А В
= (–1, )
тветы:
А В
= (–1, )
А В = (0, 4]
= (–, –1]
= (–, –1] (0, )

= (–1, 0]
= (–, )
А \ В = (–1, 0]
Пример 4.12. Даны
множества:
![]() ,
,
![]() ,
,
![]() ,
,
![]() :
:
а) Задайте перечислением множества (А В) (C D), (А В) (C D)
б) Проверьте справедливость дистрибутивного закона А (В C) = = (А В) (А C), последовательно выполняя операции в левой и правой частях равенства.
Ответы:
а) А В = {0; 4; 8}, C D = {–2; 0; 2},
(А В) (C D) = {–2;0;2;4;8},
А В = {–1; 0; 2; 4; 6; 8; 9; 10}, C D = {–2; –1; 0; 1; 2; 4},
(А В) (C D) = {–1; 0; 2; 4}.
б) В C = {–1; 0},
А (В C) = {–1; 0; 2; 4; 6; 8; 10}, А В = {–1; 0; 2; 4; 6; 8; 9; 10},
А C = {–2; –1; 0; 1; 2; 4; 6; 8; 10},
(А В) (А C) = {–1; 0; 2; 4; 6; 8; 10} = А (В C).
Пример 4.13.
Для подмножества А
= (– ;
–1], В =
[0;2] множества R
проверьте
справедливость закона
![]() ,
последовательно выполняя операции в
левой и правой частях равенства.
Изобразите на числовой оси полученные
множества.
,
последовательно выполняя операции в
левой и правой частях равенства.
Изобразите на числовой оси полученные
множества.
О тветы:
А В
=(–, –1] [0,
2]
тветы:
А В
=(–, –1] [0,
2]
![]() = (–1, 0)
(2, )
= (–1, 0)
(2, )
![]() = (–1, )
= (–1, )
![]() = (–, 0) (2, )
= (–, 0) (2, )
![]() = (–1, 0)
(2, )
= (–1, 0)
(2, )
Таким образом, = (–1, 0) (2, ).
Важной алгебраической операцией над множествами является прямое произведение. Прямым произведением множеств X и Y (обозначение X Y) называется множество упорядоченных пар
![]() ,
,
Прямым произведением множеств X, Y и Z называется множество
![]() ,
,
Известными примерами прямых произведений являются:
![]() –
плоскость;
–
плоскость;
![]() –
трехмерное пространство.
–
трехмерное пространство.
Пример 4.14. Запишите и изобразите прямое произведение, если
а)
![]() ;
б)
;
б)
![]() ;
;
в)
![]()
а)
![]() (рис. 4.8);
(рис. 4.8);
б)
![]() (рис. 4.9);
(рис. 4.9);
с)
![]() (рис. 4.10).
(рис. 4.10).

Рис. 4.8 Рис. 4.9 Рис. 4.10

 (/ / / / / / / / /)
(/ / / / / / / / /) [/ / / / / / / / / /
/ /
[/ / / / / / / / / /
/ /
 / / / / / / / / / // / /
/ / / / / / / / / // / / 


