Лекция 47 Смешение и транспортировка сыпучих материалов

47.1. Общие сведения

Процесс перемешивания зернистых (сыпучих) материалов широко применяют в различных отраслях промышленности, например, в производстве строительных материалов, при составлении шихты в коксохимии и металлургической промышленности, приготовлении красителей, лекарственных препаратов, и т. д. В некоторых процессах необходимо перемешивать грубодисперсные суспензии при большой доле твердой фазы (бетонные смеси, строительные растворы, керамические массы).

Смешение сыпучих материалов является специфическим случаем перемешивания, что обусловлено особым характером систем, состоящих из твердых частиц. В динамике такие системы ведут себя иначе, чем при перемешивании в жидких средах и поэтому требуют отдельного рассмотрения.

При смешении зернистых материалов основной задачей, как правило, является уменьшение композиционной неоднородности смеси, так как механические, физические и химические свойства, а также внешний вид изделий существенно зависят от этого параметра. Однако строгую количественную взаимосвязь между параметрами системы, способом перемешивания и его эффективностью до настоящего времени установить не удалось. Даже для бинарной системы, уравнения для оценки степени перемешивания очень сложно и требует знания многих факторов, которые трудно определить на практике.

Для оценки эффективности смесителя определяющим фактором является распределение частиц, которое достигается после определенной продолжительности гомогенизации. Мерой оценки интенсивности работы смесителя может быть или стандартное отклонение состава пробы, отобранной по истечении некоторого времени гомогенизации, или отношение действительного отклонения случайной смеси к стандартному теоретическому отклонению идеально перемешанной смеси. Второй показатель имеет то преимущество, что по мере повышения качества смешения он приближается к единице и более наглядно определяет качество смешения.

47.2. Отклонение весовой частоты пробы

Рассмотрим бинарную смесь компонентов P и Q с весовой долей каждого компонента G_P и G_Q. Состав такой смеси определяется уравнениями:

и , (47.1)

где  – концентрации отдельных компонентов смеси в долях единицы, следовательно, ,  – общее количество смеси.

Для оценки работы смесителя из общей смеси отбирают пробу небольшого объема весом . Необходимым условием является отсутствие влияния отбора пробы на общий состав и количество смеси, т. е. .

Это небольшое весовое количество также состоит из двух компонентов . Взаимное отношение обоих весовых количеств будет различным для каждой пробы.

Общий вес пробы:

. (47.2)

Общее количество смеси равно сумме всех этих малых весовых долей:

. (47.3)

Концентрации каждого компонента выражают в долях единицы в любой пробе и обозначают для компонента и для компонента . Следовательно:

; ; (47.4)

. (47.5)

В идеальной смеси сумма всех весовых долей всех проб даст соответствующее весовое количество компонентов в общей смеси:

. (47.6)

В случайной смеси значения всегда отличаются от значений, требуемых заданной степенью перемешивания и данных . В соответствии с теорией ошибок можно установить рассеяние весовых частот по сравнению с требуемыми значениями по формулам:

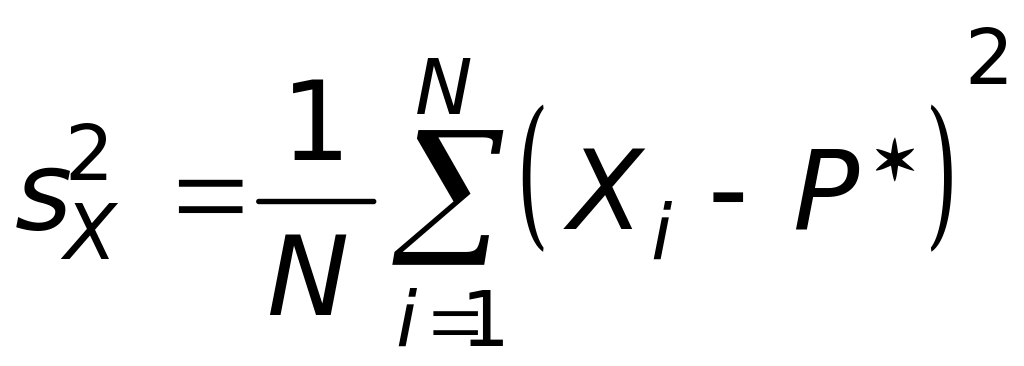; (47.7)

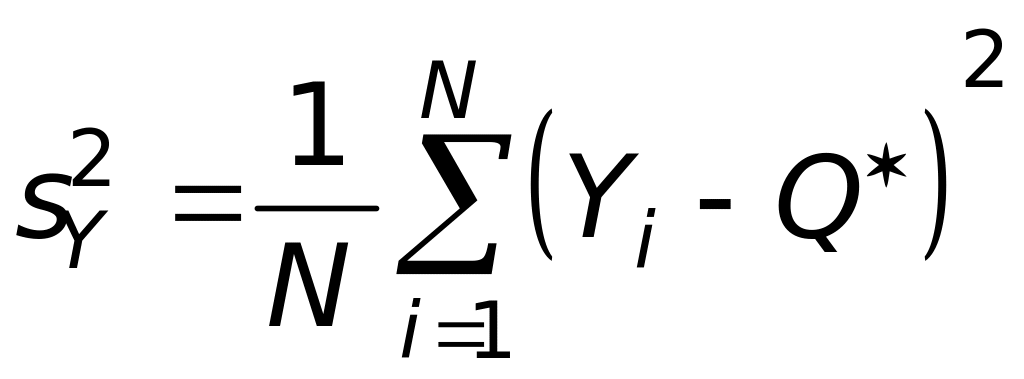, (47.8)

где  – рассеяние весовых частот от требуемого значения.

В двух последних уравнениях выражения в скобках идентичны, поэтому можно записать общее уравнение отклонения весовых частот в пробе для бинарной смеси:

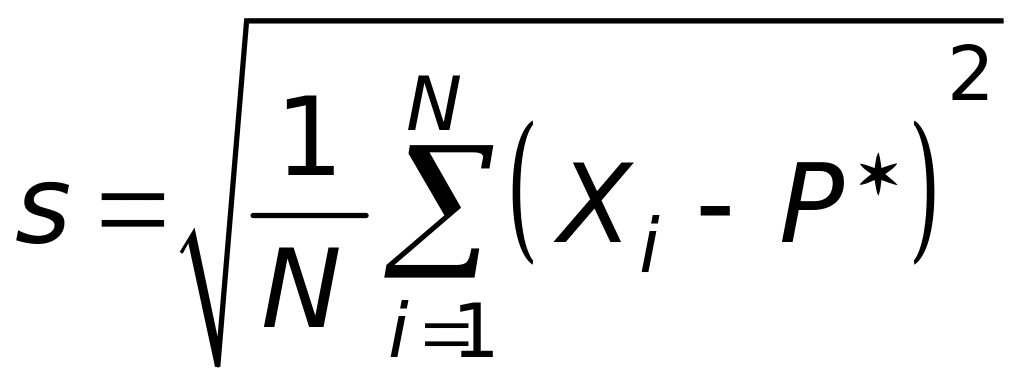. (47.9)

Уравнение (24.9) определяет отклонение произвольной смеси. Отклонение весовых частот идеальной смеси обозначим , тогда степень смешения определяется уравнением

. (47.10)

Чем ближе качество смеси к идеалу, тем ближе величина к единице.

На величину отклонения , кроме переменных, входящих в уравнение (24.9), оказывают влияние отношение веса частиц, их распределение в смеси и величина отобранной пробы.

Для получения зависимости отклонения частоты распределения частиц в уравнение (24.9) вместо переменной весовой концентрации подставим ее значение, выраженное через частоту ,

, (47.11)

где  – средний вес частиц смеси.

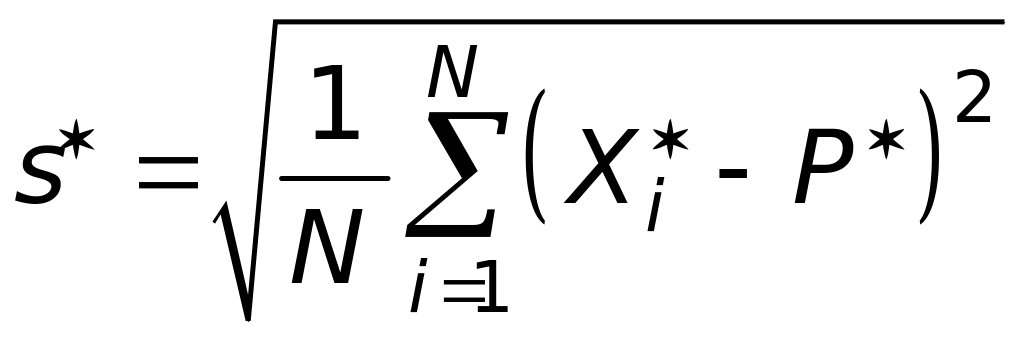. (47.12)

Для многокомпонентных смесей расчетные уравнения очень сложны и ознакомиться с ними можно в специальной литературе.

Кроме изложенного выше применяют еще несколько статистических методов оценки (количественных и качественных), имеющих применение для оценки качества зернистой смеси. Наиболее часто для этого используют распределение Стьюдента (фактор ), распределение Фишера (фактор ) и фактор (хи-квадрат).

Распределение Стьюдента позволяет оценить полноту смешения двух зернистых компонентов смеси по формуле

, (47.13)

где  – параметр распределения Стьюдента;  – среднее арифметическое значение концентрации для всех проб;  – действительная концентрация компонента во всей системе;  – стандартное отклонение системы, определяемое по уравнению

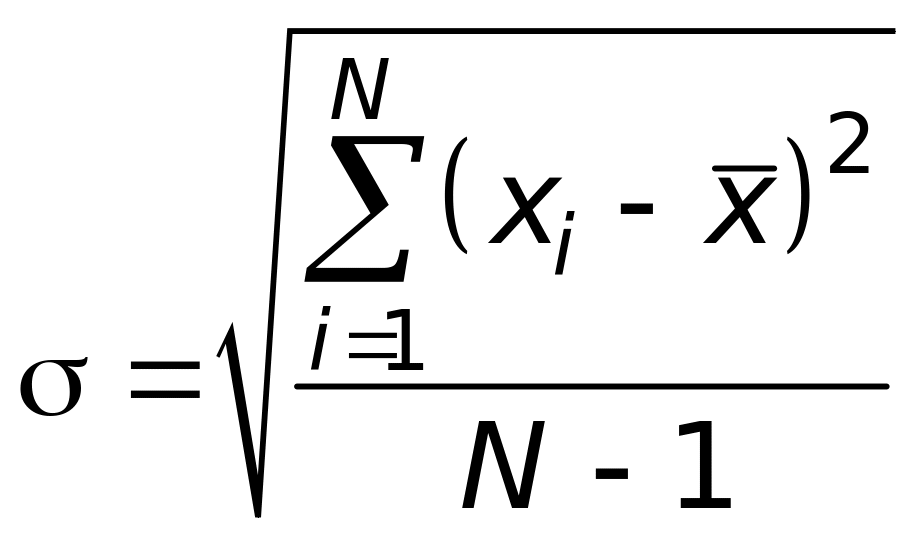, (47.14)

 – число проб;  – концентрация пробы.

Практически установлено, что при оценке качества зернистых смесей удовлетворительным является уровень доверительности 0,95. В связи с этим из таблиц величины , которые приводятся в литературе по математической статистике, определяется, может ли при числе степеней свободы полученное значение случайно встретиться чаще, чем один раз на двадцать (т. е. меньше ли значение , чем приведенное в таблице для числа степеней свободы и уровня допуска 0,05).

Распределение Фишера применяют при увеличении масштаба смесителя. Если в лабораторных условиях при степени смешения, которая считается удовлетворительной, для проб найдена дисперсия состава проб , а для смеси, полученной в промышленном аппарате, для проб найдена дисперсия состава , то фактор дает возможность оценить на данном уровне доверительности, является ли степень смешения, достигнутая в промышленном аппарате, тоже удовлетворительной. Когда , тогда статистический фактор не нужен, так как степень смешения в промышленном смесителе выше, чем в лабораторном смесителе. Если , необходимо определить отношение

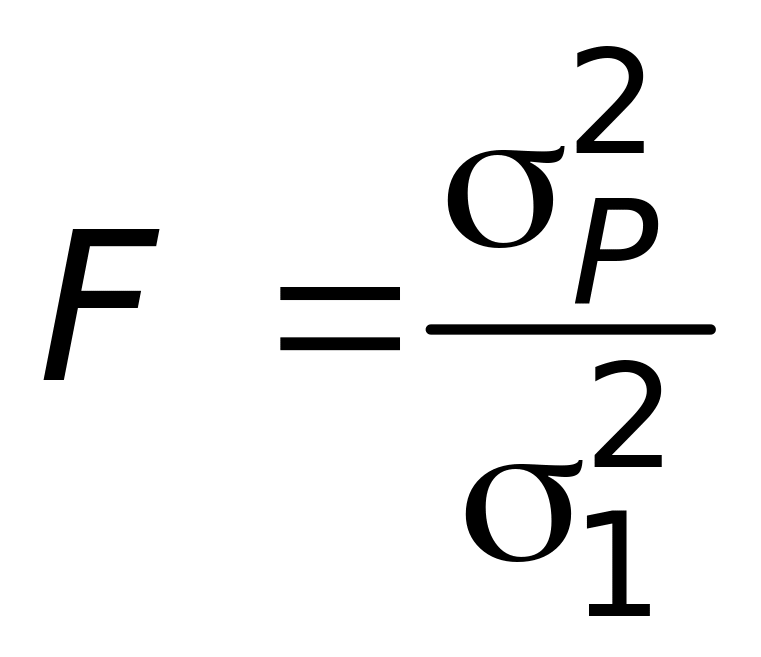. (47.15)

Рисунок 47.1– Распределение частоты состава проб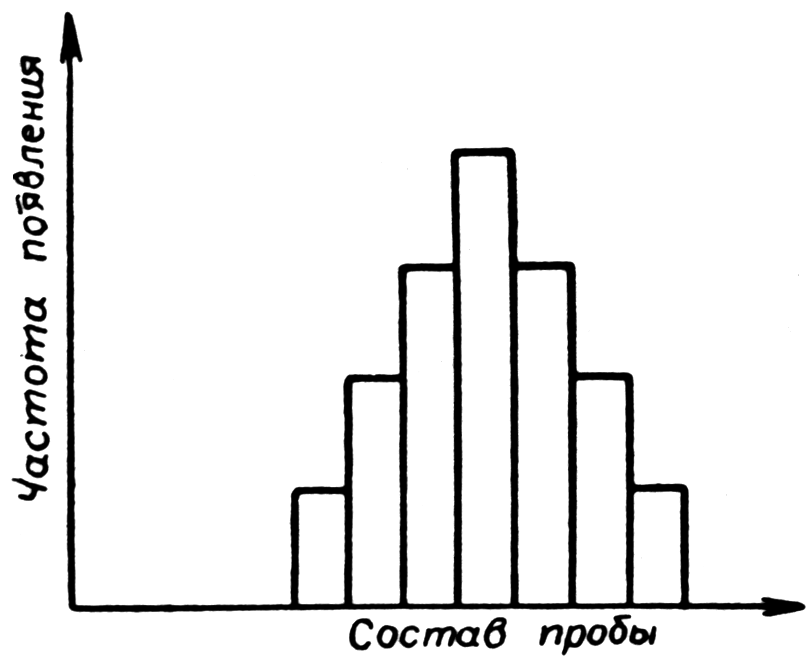

Затем из таблиц величины определяют, может ли при числах степеней свободы числителя и знаменателя, соответственно равных , такое большое значение случайно встретиться чаще, чем один раз на двадцать (т. е. меньше ли значение , чем приведенное в таблице для уровня допуска 0,05 и чисел степеней свободы ). Если значение меньше, чем приведенное в таблице, то можно заключить с 5 %-й вероятностью совершения ошибки, что смесь, полученная в промышленном смесителе, имеет удовлетворительную степень смешения.

Распределение частоты состава проб (фактор ) используют при достаточно большом числе проб, отобранных из зернистой смеси. На основании результатов анализа проб строят график (рис.47.1), на оси абсцисс которого откладывают состав (долю данного компонента в пробе), а на оси ординат – частоту его появления (число проб с данным составом). Такой график называется распределением частоты состава проб и хорошо иллюстрирует состояние смешения. Неупорядоченная смесь характеризуется нормальным распределением, а фактор позволяет оценить, является ли распределение нормальным.

Если – множество частот появления данных составов проб, а – множество соответственно ожидаемых частот, рассчитанных для данных составов по нормальному распределению, то величину определяют по уравнению

, (47.16)

где  – число пар замеченных и ожидаемых частот, которые сравниваются друг с другом (число проб должно быть подобрано так, чтобы на принятом уровне доверительности 0,95 ожидаемая частота всегда была больше или равна пяти).

Затем по таблицам определяют, может ли при числе степеней свободы такое большое значение случайно появиться чаще, чем один раз на двадцать. Если рассчитанное значение меньше, чем полученное из таблиц для уровня допуска 0,05, то можно с 5 %-й вероятностью совершения ошибки считать, что распределение частоты появления данного состава проб является нормальным распределением (т.е. в процессе операции смешения не возникли тенденции упорядочивания, вызывающие неоднородность смеси).

Гайле предложено уравнение для расчета степени смешения на основе фактора

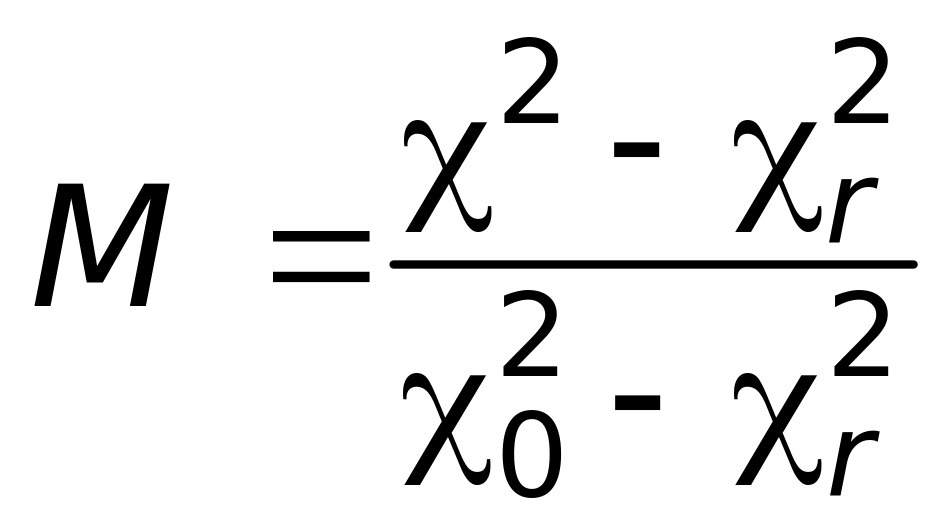, (47.17)

где  – степень смешения (изменяется от 0 для состояния полного распределения до 1 для состояния полного смешения);  – величина, рассчитанная для исследуемой смеси на основе анализа проб;  – величина, ожидаемая для состояния полного смешения;  – величина, ожидаемая для состояния полного распределения.

Следует отметить, что недостатком оценки качества смеси по параметру является необходимость анализа большого числа проб.