9.1.4. Оценка теплового потока от нагретого тела

В процессе испытаний полагается, что мощностью, теряемой нагретым телом (спиралью в вакууме) за счет процесса теплопроводности, в первом приближении можно пренебречь. Данное предположение подтверждается сравнением расчетных значений потерь за счет процессов излучения, теплопередачи, конвекции.

В результате экспериментального определения температуры Т нагретого тела яркостным пирометром с учетом закона Стефана-Больцмана (9.35) можно оценить величину интегральной энергетической светимости (интегральная излучательность) M_etс исследуемого (реального) тела:

M_etс= _тTⁿ, Вт/м², (9.50)

где n – показатель степени, в идеальном случае n = 4.

Учтем, что мощность Ф (Вт) теплового потока, испускаемого поверхностью серого тела, равна:

Ф = _т(T ⁿ – T₀ⁿ)S = S_тT ⁿ– S_тT₀ⁿ, Вт, (9.51)

где S- излучаемая поверхность, м², T₀ – температура окружающей среды, K.

Первое слагаемое _тST ⁿ = M_еTS – определяет ту часть мощности потока, которая излучается поверхностью тела, второе _тST₀ⁿ – определяет часть мощности потока, которая поглощается всей поверхностью тела за счет среды.

Поскольку в результате нагрева тело имеет фиксированную температуру Т (стационарное термическое состояние), то очевидна компенсация ″уходящей″ мощности Ф за счет подводимой активной электрической мощности Р_а, связанной с джоулевским разогревом нити током I при напряжении U. C учетом баланса мощностей в равновесном режиме имеем:

Ф = P_а = IU, (9.52)

где  < 1 – коэффициент, учитывающий, что часть электрической мощности не переходит в тепловое излучение, но ″теряется″ за счет процесса теплопроводности (через воздух, металлические контакты и т.п.).

Следовательно,

Ф = P_а = IU = _т(T ⁿ- T₀ⁿ)S. (9.53)

Соотношение (9.53) позволяет рассчитать значение интегрального коэффициента поглощения следующим образом. В реальных условиях значение Т ⁿ >> T₀ⁿ (сравним: 1000⁴ = 10¹² >> 300⁴ = 8,1·10⁹), поэтому можно записать

Ф = P = IU ≈ _тT ⁿS. (9.54)

Логарифмируя выражение (9.54) получаем:

lnФ = ln(_ттS) + nlnT. (9.55)

На основе экспериментальных данных можно построить график в двойных логарифмических координатах lnФ(lnT) (рис. 9.3, а) и расчетным путем получить средние значения _т и n:

n_ср = lnФ/lnT; (9.56)

_{т ср}= e^lnФ/S, (9.57)

где величина lnФ определяется графически путем экстраполяции линии тренда функции lnФ(lnT) к оси ординат (рис. 9.2, а).

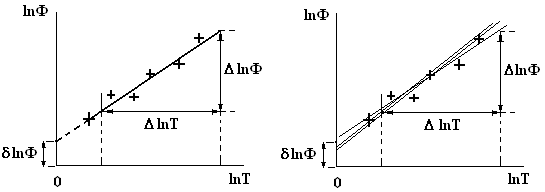
а) б)

Рис. 9.2. Определение значений n и _т

Заметим, что обработка зависимости lnP(lnT) с помощью пакета Excel позволяет с помощью линии тренда определить не только значение n_ср, но и параметр lnФ = ln(_ттS).

Погрешность эксперимента оценивается путем варьирования линии тренда (рис. 9.2, б) и расчета погрешности n и _т постоянных n и _т, так что результат записывается в виде: n = n_ср ± n; _{т ср} = _т ± _т.